1.5 वास्तविक संख्याओं के लिए घातांक-नियम (Laws of Exponents for Real Numbers)
MP Board 9th Laws of Exponents for Real Numbers : MP Board 9th Laws of Exponents for Real Numbers वास्तविक संख्याओं के लिए घातांक-नियम
प्रश्नावली 1.5 (Exercise 1.5)
1. ज्ञात कीजिए (Find the value of):
(i) ![]()
- Solution: We know that
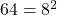 .
.![Rendered by QuickLaTeX.com \[(8^2)^{\frac{1}{2}} = 8^{2 \times \frac{1}{2}} = 8^1 = 8\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-49f3c1910bd5b5909599dedd5e942625_l3.png)
(ii) ![]()
- Solution: We know that
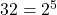 .
.![Rendered by QuickLaTeX.com \[(2^5)^{\frac{1}{5}} = 2^{5 \times \frac{1}{5}} = 2^1 = 2\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-8ba97db83463536dfb9b61fc933ef638_l3.png)
(iii) ![]()
- Solution: We know that
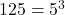 .
.![Rendered by QuickLaTeX.com \[(5^3)^{\frac{1}{3}} = 5^{3 \times \frac{1}{3}} = 5^1 = 5\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-92645a033d896e30abffc933cf7023c6_l3.png)
2. ज्ञात कीजिए (Find the value of):
(i) ![]()
- Solution: We know that
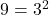 .
.![Rendered by QuickLaTeX.com \[(3^2)^{\frac{3}{2}} = 3^{2 \times \frac{3}{2}} = 3^3 = 27\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-b7863b6bf07d31cae990a2550a5f0382_l3.png)
(ii) ![]()
- Solution: We know that
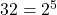 .
.![Rendered by QuickLaTeX.com \[(2^5)^{\frac{2}{5}} = 2^{5 \times \frac{2}{5}} = 2^2 = 4\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-8f696c49f00bf0d15137cde058993433_l3.png)
(iii) ![]()
- Solution: We know that
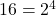 .
.![Rendered by QuickLaTeX.com \[(2^4)^{\frac{3}{4}} = 2^{4 \times \frac{3}{4}} = 2^3 = 8\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-19f266cc60546b0e15bcf33f51d93641_l3.png)
(iv) ![]()
- Solution: We know that
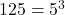 . Using the rule
. Using the rule 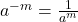 .
.![Rendered by QuickLaTeX.com \[(5^3)^{\frac{-1}{3}} = 5^{3 \times \frac{-1}{3}} = 5^{-1} = \frac{1}{5}\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-bda5a5f41c5dbb586a054cf078a84776_l3.png)
3. सरल कीजिए (Simplify):
(i) ![]()
- Solution: Using the rule
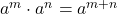 .
.![Rendered by QuickLaTeX.com \[2^{\frac{2}{3} + \frac{1}{5}} = 2^{\frac{10+3}{15}} = 2^{\frac{13}{15}}\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-5012d595e2af6b9690bea7be2e30ea04_l3.png)
(ii) ![]()
- Solution: Using the rule
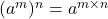 .
.![Rendered by QuickLaTeX.com \[\frac{1^7}{(3^3)^7} = \frac{1}{3^{3 \times 7}} = \frac{1}{3^{21}} \quad \text{or} \quad 3^{-21}\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-3c20ad8d6898943db6e1484e88d63a0d_l3.png)
(iii) ![]()
- Solution: Using the rule
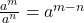 .
.![Rendered by QuickLaTeX.com \[11^{\frac{1}{2} - \frac{1}{4}} = 11^{\frac{2-1}{4}} = 11^{\frac{1}{4}}\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-1c6b4b7091c92ab91514488ba03fb41f_l3.png)
(iv) ![]()
- Solution: Using the rule
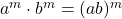 .
.![Rendered by QuickLaTeX.com \[(7 \times 8)^{\frac{1}{2}} = 56^{\frac{1}{2}}\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-85380c93e175495701593bf132204c0e_l3.png)