बहुपद के शून्यकों का ज्यामितीय अर्थ : MP Board 10th Mathematics Geometrical Meaning of Polynomial
MP Board 10th Mathematics Geometrical Meaning of Polynomial : गणित में किसी बहुपद (Polynomial) के शून्यक (Zero) वे संख्याएँ होती हैं जिनके लिए बहुपद का मान 0 हो जाता है। इनका ज्यामितीय अर्थ ग्राफ के संदर्भ में समझा जाता है—यह उन बिंदुओं का प्रतिनिधित्व करता है जहाँ बहुपद का ग्राफ x-अक्ष को काटता है।
शून्यकों का परिभाषा
यदि कोई बहुपद ( P(x) ) दिया गया हो, तो उसका शून्यक वह मान ( x ) होगा जिसके लिए:
( P(x) = 0 )
यह x-अक्ष पर बहुपद ग्राफ के छूने या काटने वाले बिंदु को दर्शाता है।
ज्यामितीय अर्थ
बहुपद ( P(x) ) के शून्यकों को x-अक्ष पर ग्राफ के साथ इसके प्रतिच्छेद (intersection points) के रूप में देखा जा सकता है।
- यदि किसी बहुपद का एक शून्यक है, तो वह ग्राफ x-अक्ष को एक बिंदु पर काटता है।
- यदि बहुपद के एक से अधिक शून्यक हैं, तो ग्राफ कई स्थानों पर x-अक्ष को काटता है।
- यदि कोई शून्यक दोहराया जाता है, तो ग्राफ x-अक्ष को स्पर्श करता है लेकिन पार नहीं करता।
उदाहरण और स्पष्टीकरण
1. रैखिक बहुपद (Linear Polynomial)
बहुपद: ( P(x) = x – 3 )
शून्यक: ( P(3) = 3 – 3 = 0 )
ज्यामितीय व्याख्या:
- इस बहुपद का ग्राफ एक सीधी रेखा है।
- यह x-अक्ष को (3,0) बिंदु पर काटता है।
2. द्विघात बहुपद (Quadratic Polynomial)
द्विघात समीकरण (quadratic equation) ![]() को हल करने के सही चरण :
को हल करने के सही चरण :
- समीकरण (Equation):
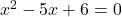
- गुणनखंड (Factoring):आपने इसे
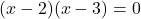 के रूप में सही गुणनखंड किया है। (इसे “मध्य पद को तोड़कर” या “middle-term splitting” भी कहते हैं, जहाँ -2 और -3 को जोड़ने पर -5 और गुणा करने पर +6 आता है)।
के रूप में सही गुणनखंड किया है। (इसे “मध्य पद को तोड़कर” या “middle-term splitting” भी कहते हैं, जहाँ -2 और -3 को जोड़ने पर -5 और गुणा करने पर +6 आता है)। - हल (Solutions/Roots):शून्य गुणनफल गुण (Zero Product Property) के अनुसार, यदि
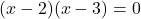 है, तो:
है, तो:
- या तो
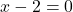 , जिससे
, जिससे 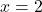 मिलता है।
मिलता है। - या
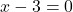 , जिससे
, जिससे 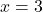 मिलता है।
मिलता है।
- या तो
आपके हल ![]() और
और ![]() एकदम सही हैं।
एकदम सही हैं।
ये मान (2 और 3) बहुपद ![]() के शून्यक (zeros) कहलाते हैं। यह आपकी पिछली प्रश्नावली 2.1 के विषय से जुड़ा है: अगर आप
के शून्यक (zeros) कहलाते हैं। यह आपकी पिछली प्रश्नावली 2.1 के विषय से जुड़ा है: अगर आप ![]() का ग्राफ बनाएँगे, तो वह
का ग्राफ बनाएँगे, तो वह ![]() -अक्ष को
-अक्ष को ![]() और
और ![]() पर काटेगा (जैसा कि चित्र (iv) में दिखाया गया था, जिसके दो शून्यक थे)।
पर काटेगा (जैसा कि चित्र (iv) में दिखाया गया था, जिसके दो शून्यक थे)।
3. घनात्मक बहुपद (Cubic Polynomial)
आइए इस त्रिघात बहुपद (cubic polynomial) के शून्यक (zeros) ज्ञात करते हैं।
![]()
द्विघात समीकरण के विपरीत, त्रिघात समीकरणों को हल करने के लिए हम गुणनखंड प्रमेय (Factor Theorem) और बहुपद विभाजन (Polynomial Division) का उपयोग करते हैं।
चरण 1: पहला शून्यक ढूँढना (गुणनखंड प्रमेय)
हम ![]() के लिए कुछ सरल मान (जैसे
के लिए कुछ सरल मान (जैसे ![]() जो 6 के गुणनखंड हैं) रखकर
जो 6 के गुणनखंड हैं) रखकर ![]() का मान
का मान ![]() आता है या नहीं, यह जाँचेंगे।
आता है या नहीं, यह जाँचेंगे।
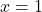 रखने पर:
रखने पर: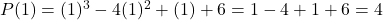 यह
यह 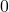 नहीं है, इसलिए
नहीं है, इसलिए  एक गुणनखंड नहीं है।
एक गुणनखंड नहीं है।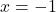 रखने पर:
रखने पर: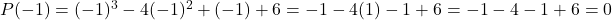 यह
यह 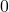 है! 🎉
है! 🎉
- इसलिए,
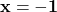 इस बहुपद का पहला शून्यक है।
इस बहुपद का पहला शून्यक है। - इसका मतलब है कि
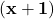 बहुपद का एक गुणनखंड है।
बहुपद का एक गुणनखंड है।
- इसलिए,
चरण 2: बहुपद को भाग देना (Polynomial Division)
अब जब हमें एक गुणनखंड ![]() मिल गया है, तो हम मूल बहुपद
मिल गया है, तो हम मूल बहुपद ![]() को
को ![]() से भाग देकर शेष गुणनखंडों का पता लगा सकते हैं।
से भाग देकर शेष गुणनखंडों का पता लगा सकते हैं।
![]()
भाग देने पर हमें भागफल (quotient) ![]() मिलता है।
मिलता है।
(आप इसे बहुपद दीर्घ विभाजन (polynomial long division) या संश्लेषित विभाजन (synthetic division) से सत्यापित कर सकते हैं।)
इसका मतलब है कि हम बहुपद को इस प्रकार लिख सकते हैं:
![]()
चरण 3: शेष द्विघात समीकरण को हल करना
अब हमें ![]() करने के लिए शेष भाग
करने के लिए शेष भाग ![]() को
को ![]() के बराबर रखना है:
के बराबर रखना है:
![]()
यह वही समीकरण है जिसे आपने पिछले प्रश्न में हल किया था! इसके गुणनखंड हैं:
![]()
इससे हमें दो और शून्यक मिलते हैं:
अंतिम उत्तर
बहुपद ![]() के तीन शून्यक हैं:
के तीन शून्यक हैं:
-1, 2, और 3
ज्यामितीय व्याख्या:
- इसका ग्राफ एक घनात्मक वक्र (Cubic Curve) है।
- यह x-अक्ष को तीन बिंदुओं (-1,0), (2,0), (3,0) पर काटता है।
निष्कर्ष
बहुपद के शून्यक ज्यामितीय रूप से x-अक्ष के साथ ग्राफ के प्रतिच्छेद को दर्शाते हैं। रैखिक बहुपद में एक शून्यक, द्विघात में अधिकतम दो, और घनात्मक में तीन शून्यक होते हैं। इनका अध्ययन गणित, भौतिकी और इंजीनियरिंग में महत्वपूर्ण है।
प्रश्नावली 2.1 (Exercise 2.1)
यहाँ दिए गए प्रश्न का हल है:
किसी बहुपद ![]() के शून्यकों की संख्या, ग्राफ पर उन बिंदुओं की संख्या के बराबर होती है, जहाँ
के शून्यकों की संख्या, ग्राफ पर उन बिंदुओं की संख्या के बराबर होती है, जहाँ ![]() का ग्राफ
का ग्राफ ![]() -अक्ष (X-axis) को प्रतिच्छेद (intersect) या स्पर्श (touch) करता है।
-अक्ष (X-axis) को प्रतिच्छेद (intersect) या स्पर्श (touch) करता है।
इस आधार पर, प्रत्येक स्थिति में शून्यकों की संख्या निम्नलिखित है:
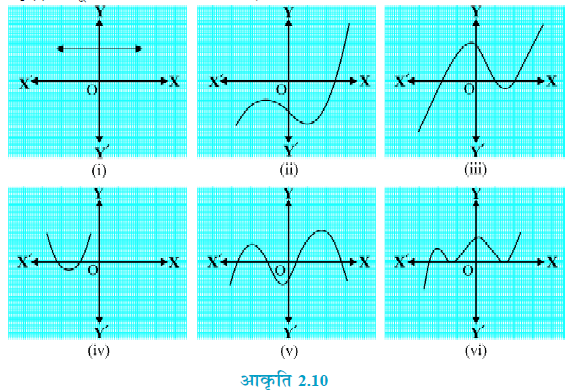
- (i) ग्राफ
 -अक्ष को किसी भी बिंदु पर नहीं काटता है।
-अक्ष को किसी भी बिंदु पर नहीं काटता है।
- शून्यकों की संख्या = 0
- (ii) ग्राफ
 -अक्ष को केवल एक बिंदु पर काटता है।
-अक्ष को केवल एक बिंदु पर काटता है।
- शून्यकों की संख्या = 1
- (iii) ग्राफ
 -अक्ष को तीन बिंदुओं पर काटता है।
-अक्ष को तीन बिंदुओं पर काटता है।
- शून्यकों की संख्या = 3
- (iv) ग्राफ
 -अक्ष को दो बिंदुओं पर काटता है।
-अक्ष को दो बिंदुओं पर काटता है।
- शून्यकों की संख्या = 2
- (v) ग्राफ
 -अक्ष को चार बिंदुओं पर काटता है।
-अक्ष को चार बिंदुओं पर काटता है।
- शून्यकों की संख्या = 4
- (vi) ग्राफ
 -अक्ष को तीन बिंदुओं पर (एक बिंदु पर काटते हुए और दो बिंदुओं पर स्पर्श करते हुए) मिलता है।
-अक्ष को तीन बिंदुओं पर (एक बिंदु पर काटते हुए और दो बिंदुओं पर स्पर्श करते हुए) मिलता है।
- शून्यकों की संख्या = 3