यदि दो संख्याओं का HCF $1$ हो, तो उन संख्याओं को क्या कहते हैं?

जिन दो संख्याओं का HCF $1$ होता है, उन्हें सह-अभाज्य संख्याएं (Co-prime Numbers) कहा जाता है। उदाहरण: $8$ और $15$ (दोनों भाज्य हैं, लेकिन इनमें $1$ के अलावा कोई कॉमन गुणनखंड नहीं है)।

10th Maths Fundamental Theorem of Arithmetic : अंकगणित की आधारभूत प्रमेय

Q: अंकगणित की आधारभूत प्रमेय का गणित में क्या महत्व है?

यह प्रमेय गणित का वह नियम है जो साबित करता है कि हर भाज्य संख्या का एक "अद्वितीय DNA" (अभाज्य गुणनखंड) होता है। इसके बिना भिन्न (Fractions) को सरल करना, HCF, और LCM निकालना असंभव होता।

Q: Word Problems में यह कैसे पहचानें कि HCF निकालना है या LCM?

HCF की पहचान: जब प्रश्न में किसी चीज़ को "समान और अधिकतम बड़े भागों में बाँटने", "अधिकतम क्षमता", या "न्यूनतम स्थान घेरने" (जिसका अर्थ अधिकतम स्टैक बनाना हो) की बात हो, तो HCF निकालें। LCM की पहचान: जब प्रश्न में "घटनाएं एक साथ कब होंगी", "न्यूनतम समय", "एक ही बिंदु पर पुनः कब मिलेंगे" (जैसे दौड़ना, घंटियां बजना, ट्रैफिक लाइट बदलना) की बात हो, तो LCM निकालें।

Q: क्या $1$ एक अभाज्य (Prime) संख्या है?

नहीं, $1$ न तो अभाज्य संख्या है और न ही भाज्य संख्या है। यह एक विशिष्ट (Unique) संख्या है। अभाज्य संख्या की परिभाषा के अनुसार उसके ठीक दो गुणनखंड ($1$ और वह स्वयं) होने चाहिए, जबकि $1$ का केवल एक ही गुणनखंड है।

परिभाषा (Definition)

10th Maths Fundamental Theorem of Arithmetic : अंकगणित की आधारभूत प्रमेय (Fundamental Theorem of Arithmetic) के अनुसार, प्रत्येक संमिश्र संख्या (Composite Number), जो 1 से बड़ी हो, को अभाज्य संख्याओं (Prime Numbers) के गुणनफल के रूप में एकमात्र (Unique) तरीके से व्यक्त किया जा सकता है, बशर्ते अभाज्य संख्याओं के क्रम को न माना जाए।

अभाज्य संख्या (Prime Number): ऐसी संख्या जो केवल 1 और स्वयं से विभाज्य हो, जैसे 2, 3, 5, 7, 11।
संमिश्र संख्या (Composite Number): ऐसी संख्या जो 1, स्वयं, और कम से कम एक अन्य संख्या से विभाज्य हो, जैसे 4, 6, 8, 15।

यह प्रमेय इस बात की गारंटी देता है कि किसी भी संमिश्र संख्या का अभाज्य गुणनखंडन (Prime Factorization) अद्वितीय (Unique) होता है, चाहे उसे किसी भी तरह से तोड़ा जाए।

विस्तृत व्याख्या (Detailed Explanation)

अभाज्य गुणनखंडन (Prime Factorization): किसी संमिश्र संख्या को बार-बार अभाज्य संख्याओं से विभाजित करके उसे अभाज्य संख्याओं के गुणनफल के रूप में लिखा जाता है।
- उदाहरण: 36 को अभाज्य संख्याओं में तोड़ने पर 36 = 2 × 2 × 3 × 3 = 2² × 3²। यह एकमात्र तरीका है (क्रम को छोड़कर, जैसे 3 × 2 × 3 × 2 भी वही है)।
अद्वितीयता (Uniqueness): प्रमेय का सबसे महत्वपूर्ण हिस्सा यह है कि गुणनखंडन का परिणाम हमेशा एक ही होता है। उदाहरण के लिए, 100 को हमेशा 2² × 5² के रूप में ही लिखा जाएगा।
संख्या 1 का स्थान: 1 न तो अभाज्य है और न ही संमिश्र, इसलिए यह प्रमेय 1 पर लागू नहीं होता।
अभाज्य संख्याएं: अभाज्य संख्याएं (जैसे 7, 13) स्वयं अपने गुणनखंड के रूप में अद्वितीय होती हैं।

यह प्रमेय गणित में संख्याओं की संरचना को समझने का आधार है और विभिन्न गणितीय अवधारणाओं, जैसे HCF, LCM, और भिन्नों के सरलीकरण में उपयोगी है।

WhatsApp Channel Join Now

Telegram Channel Join Now

उदाहरण (10th Maths Fundamental Theorem of Arithmetic)

संख्या 48 का अभाज्य गुणनखंडन:
- 48 को अभाज्य संख्याओं में तोड़ें:
  48 ÷ 2 = 24
  24 ÷ 2 = 12
  12 ÷ 2 = 6
  6 ÷ 2 = 3
  3 ÷ 3 = 1
- इसलिए, 48 = 2 × 2 × 2 × 2 × 3 = 2⁴ × 3
- यह गुणनखंडन अद्वितीय है।
संख्या 180 का अभाज्य गुणनखंडन:
- 180 को अभाज्य संख्याओं में तोड़ें:
  180 ÷ 2 = 90
  90 ÷ 2 = 45
  45 ÷ 3 = 15
  15 ÷ 3 = 5
  5 ÷ 5 = 1
- इसलिए, 180 = 2 × 2 × 3 × 3 × 5 = 2² × 3² × 5
- यह गुणनखंडन भी अद्वितीय है।
संख्या 29 का अभाज्य गुणनखंडन:
- 29 एक अभाज्य संख्या है, इसलिए इसका गुणनखंडन केवल 29 है।
- यह भी प्रमेय के अनुसार अद्वितीय है।
संख्या 225 का अभाज्य गुणनखंडन:
- 225 को अभाज्य संख्याओं में तोड़ें:
  225 ÷ 3 = 75
  75 ÷ 3 = 25
  25 ÷ 5 = 5
  5 ÷ 5 = 1
- इसलिए, 225 = 3 × 3 × 5 × 5 = 3² × 5²
- यह गुणनखंडन अद्वितीय है।

उपयोग (Applications)

महत्तम समापवर्तक (HCF) और लघुत्तम समापवर्तक (LCM):
- अभाज्य गुणनखंडन का उपयोग करके HCF और LCM निकाला जाता है।
- उदाहरण: 24 और 36 का HCF और LCM:
  - 24 = 2³ × 3
  - 36 = 2² × 3²
  - HCF = 2² × 3 = 12 (सामान्य अभाज्य संख्याओं का न्यूनतम घात)
  - LCM = 2³ × 3² = 72 (सभी अभाज्य संख्याओं का अधिकतम घात)
भिन्नों का सरलीकरण:
- उदाहरण: 36/48 को सरल करें।
  - 36 = 2² × 3², 48 = 2⁴ × 3
  - HCF = 2² × 3 = 12
  - 36 ÷ 12 = 3, 48 ÷ 12 = 4
  - इसलिए, 36/48 = 3/4
संख्या सिद्धांत (Number Theory):
- यह प्रमेय संख्याओं के गुणों, जैसे विभाज्यता और गुणनखंडन, को समझने में मदद करता है।
- यह क्रिप्टोग्राफी और अन्य उन्नत गणितीय क्षेत्रों में भी उपयोगी है।
वास्तविक जीवन में उपयोग:
- समय, दूरी, या मात्रा से संबंधित समस्याओं में, जैसे दो व्यक्तियों के मिलने का समय (LCM) या सामान्य कार्य का हिस्सा (HCF)।

विशेष बिंदु (Key Points)

अंकगणित की आधारभूत प्रमेय केवल 1 से बड़ी संमिश्र संख्याओं (Composite Numbers) और अभाज्य संख्याओं (Prime Numbers) पर लागू होती है।
संख्या 1 न तो अभाज्य है और न ही संमिश्र, इसलिए यह प्रमेय का हिस्सा नहीं है।
अभाज्य गुणनखंडन की अद्वितीयता संख्याओं की मूलभूत संरचना को दर्शाती है।
यह प्रमेय गणित में HCF, LCM, और अन्य अवधारणाओं का आधार बनता है।

See Notes here : MP Board digital Library

उदाहरण 3: 96 और 404 का HCF तथा LCM ज्ञात कीजिए  
हल:  
अभाज्य गुणनखंडन: 


महत्तम समापवर्तक (HCF):
सामान्य अभाज्य गुणनखंड:   
सबसे छोटी घात: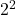   

लघुत्तम समापवर्तक (LCM): 
सभी अभाज्य गुणनखंडों की सबसे बड़ी घात:  


उदाहरण 4: 6, 72 और 120 का HCF तथा LCM ज्ञात कीजिए  
हल:
अभाज्य गुणनखंडन: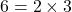
  
 

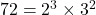
महत्तम समापवर्तक (HCF):
सामान्य अभाज्य गुणनखंड: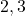   
सबसे छोटी घात: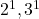   

लघुत्तम समापवर्तक (LCM):  
सभी अभाज्य गुणनखंडों की सबसे बड़ी घात:  

📌 **टिप्पणी:**  
तीन संख्याओं का गुणनफल उनके HCF और LCM के गुणनफल के बराबर नहीं होता।

 प्रश्नावली 1.1 (Fundamental Theorem of Arithmatic)

 प्रश्न 1: अभाज्य गुणनखंडन करें:  
(i)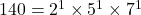   
(ii)   
(iii)   
(iv)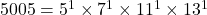   
(v) 

प्रश्न 2: HCF और LCM ज्ञात करें

(i) 26 और 91
  
✔   
✔   
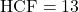
✔ जाँच: 

(ii) 510 और 92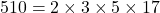
  
  
✔   
✔   
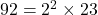
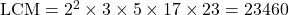
✔ जाँच: 

(iii) 336 और 54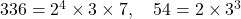  
  
✔   
✔   
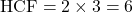
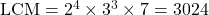
✔ जाँच: 

(iv) 12, 15 और 21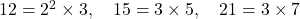  
  
✔   
✔ 

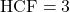
(v) 17, 23 और 29 
✔ सभी अभाज्य संख्याएँ हैं  
✔ 

(vi) 8, 9 और 25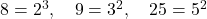 
  
✔ 

प्रश्न 4: HCF और LCM (306, 657)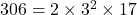
  
  
✔   
✔ 

प्रश्न 5: संख्या  का अंतिम अंक 0 हो सकता है?
✔ किसी संख्या का अंतिम अंक 0 तभी होता है जब वह 10 का गुणज हो।  
✔ , जबकि  
  
✅ अतः  कभी भी 0 पर समाप्त नहीं हो सकता।

 प्रश्न 6:  
****  
✔ यह 2 से विभाज्य है, इसलिए **अभाज्य नहीं**।
****  
✔ यह 5 से विभाज्य है, इसलिए **अभाज्य नहीं**।

प्रश्न 7: सोनिया और रवि कब मिलेंगे?
✔ सोनिया = 18 मिनट में एक चक्कर  
✔ रवि = 12 मिनट में एक चक्कर  
✔ 
✅ **36 मिनट बाद वे एक ही स्थान पर मिलेंगे।**

Useful for Lower Grade Students

अंकगणित की आधारभूत प्रमेय (Fundamental Theorem of Arithmetic) –

Class 10 Mathematics Chapter 1: Real Numbers में सबसे महत्वपूर्ण और बोर्ड परीक्षा के दृष्टिकोण से सबसे ज्यादा पूछे जाने वाला विषय है अंकगणित की आधारभूत प्रमेय (Fundamental Theorem of Arithmetic)। यदि आप कक्षा 10वीं के छात्र हैं और बोर्ड परीक्षा (CBSE, UP Board, MP Board, BSEB) में गणित में पूरे अंक लाना चाहते हैं, तो यह आर्टिकल आपके लिए संजीवनी बूटी है।

इस विस्तृत नोट्स में हम जानेंगे कि यह प्रमेय क्या है, इसका उपयोग कैसे होता है, अभाज्य गुणनखंडन (Prime Factorization) कैसे करें, और HCF/LCM से जुड़े सबसे मुश्किल Word Problems को कैसे हल करें।

1. अंकगणित की आधारभूत प्रमेय क्या है? (What is Fundamental Theorem of Arithmetic?)

1.1 प्रमेय का आधिकारिक कथन (Official Statement)

“प्रत्येक भाज्य संख्या (Composite Number) को अभाज्य संख्याओं (Prime Numbers) के एक अद्वितीय गुणनफल के रूप में व्यक्त (गुणनखंडित) किया जा सकता है, बशर्ते हम अभाज्य गुणनखंडों के आने वाले क्रम पर ध्यान न दें।”

1.2 सरल शब्दों में व्याख्या (Simple Explanation)

इस दुनिया में कोई भी भाज्य संख्या (जिसके 2 से अधिक गुणनखंड हों, जैसे 4, 6, 12, 50, 100) वास्तव में अभाज्य संख्याओं (जैसे 2, 3, 5, 7, 11…) से मिलकर बनी होती है। अभाज्य संख्याएं गणित की दुनिया के “परमाणु” (Atoms) या “बिल्डिंग ब्लॉक्स” हैं।

जब हम किसी संख्या को तोड़ते हैं, तो अंत में केवल अभाज्य संख्याएं ही बचती हैं।

“अद्वितीय” (Unique) का क्या अर्थ है?

अद्वितीय का मतलब है कि किसी संख्या का अभाज्य गुणनखंडन पूरी दुनिया में एक ही होगा।

उदाहरण के लिए, $30$ के अभाज्य गुणनखंड हमेशा $2 \times 3 \times 5$ ही होंगे।
आप क्रम बदल सकते हैं ( $5 \times 3 \times 2$ या $3 \times 2 \times 5$ ), लेकिन संख्याएं (2, 3 और 5) कभी नहीं बदलेंगी। यदि हम इन्हें आरोही क्रम (Ascending order) में लिखें, तो यह पूरी तरह अद्वितीय हो जाता है।

2. अभाज्य गुणनखंडन के बेहतरीन उदाहरण (Extra Examples of Prime Factorization)

आइए इस प्रमेय को कुछ नए और शानदार उदाहरणों से समझते हैं:

उदाहरण 1: संख्या 360 का अभाज्य गुणनखंडन करें।

360 को सबसे छोटी अभाज्य संख्या 2 से भाग दें: $360 \div 2 = 180$
180 को 2 से भाग दें: $180 \div 2 = 90$
90 को 2 से भाग दें: $90 \div 2 = 45$
अब 45, 2 से नहीं कटेगा, तो 3 से दें: $45 \div 3 = 15$
15 को 3 से दें: $15 \div 3 = 5$
अंत में 5 को 5 से दें: $5 \div 5 = 1$ उत्तर: $360 = 2 \times 2 \times 2 \times 3 \times 3 \times 5 = 2^3 \times 3^2 \times 5^1$

उदाहरण 2: संख्या 1001 का अभाज्य गुणनखंडन करें।

यह संख्या बोर्ड परीक्षाओं में अक्सर कंफ्यूज करने के लिए दी जाती है।

यह 2, 3, 5 से नहीं कटती। 7 से प्रयास करें: $1001 \div 7 = 143$
अब 143, 11 से कटेगा: $143 \div 11 = 13$
13 एक अभाज्य संख्या है: $13 \div 13 = 1$ उत्तर: $1001 = 7 \times 11 \times 13$

3. प्रमेय के मुख्य अनुप्रयोग (Important Applications of the Theorem)

इस प्रमेय के गणित में तीन सबसे बड़े उपयोग हैं:

A. HCF और LCM ज्ञात करना (Finding HCF & LCM)

HCF (महत्तम समापवर्तक): दी गई संख्याओं के अभाज्य गुणनखंडों में से केवल उभयनिष्ठ (Common) गुणनखंडों की सबसे छोटी घातों (Smallest Powers) का गुणनफल।
LCM (लघुत्तम समापवर्त्य): दी गई संख्याओं के अभाज्य गुणनखंडों में उपस्थित सभी अभाज्य गुणनखंडों की सबसे बड़ी घातों (Highest Powers) का गुणनफल।

महत्वपूर्ण जादुई सूत्र (Magic Formula):

(केवल किन्हीं दो संख्याओं $a$ और $b$ के लिए)

$HCF(a, b) \times LCM(a, b) = a \times b$

B. संख्या के अंत में शून्य (0) आने की शर्त

किसी भी संख्या (जैसे $a^n$ ) का अंतिम अंक शून्य ( $0$ ) तभी होगा, जब उसके आधार ( $a$ ) के अभाज्य गुणनखंडों में कम से कम एक बार $2$ और $5$ दोनों अनिवार्य रूप से मौजूद हों। क्योंकि $2 \times 5 = 10$ होता है।

C. भाज्य संख्या की जांच

यदि हम किसी बड़ी सी दिखने वाली संख्या (जैसे $7 \times 11 \times 13 + 13$ ) को अभाज्य संख्याओं के गुणनफल के रूप में दर्शा सकें, तो हम सिद्ध कर सकते हैं कि वह एक भाज्य संख्या है।

4. Board Exam PYQs & Word Problems (पिछले वर्षों के सबसे महत्वपूर्ण प्रश्न)

यहाँ वे प्रश्न दिए गए हैं जो बोर्ड परीक्षाओं में 3 से 4 अंकों में पूछे जाते हैं।

प्रश्न 1: तीन संख्याओं का HCF और LCM (Basic Application)

प्रश्न: अभाज्य गुणनखंडन विधि द्वारा $12, 15$ और $21$ का HCF और LCM ज्ञात कीजिए। (CBSE 2019)

हल:

सबसे पहले अभाज्य गुणनखंडन करेंगे:

$12 = 2 \times 2 \times 3 = 2^2 \times 3^1$

$15 = 3 \times 5 = 3^1 \times 5^1$

$21 = 3 \times 7 = 3^1 \times 7^1$

HCF: तीनों में केवल $3$ उभयनिष्ठ (common) है और उसकी सबसे छोटी घात $1$ है। $HCF = 3^1 = 3$
LCM: सभी अभाज्य गुणनखंडों ( $2, 3, 5, 7$ ) की सबसे बड़ी घातें लेंगे। $LCM = 2^2 \times 3^1 \times 5^1 \times 7^1 = 4 \times 3 \times 5 \times 7 = 420$ उत्तर: HCF = $3$ , LCM = $420$ .

प्रश्न 2: शून्य पर समाप्त होने वाली संख्या (Conceptual VVI)

प्रश्न: जाँच कीजिए कि क्या किसी प्राकृत संख्या $n$ के लिए, संख्या $4^n$ अंक $0$ पर समाप्त हो सकती है? (NCERT)

हल:

किसी संख्या के $0$ पर समाप्त होने के लिए, उसके अभाज्य गुणनखंड में $2$ और $5$ दोनों का होना आवश्यक है।

संख्या $4^n$ का अभाज्य गुणनखंडन:

$4^n = (2^2)^n = 2^{2n}$

यहाँ हम देखते हैं कि $4^n$ के अभाज्य गुणनखंड में केवल $2$ मौजूद है। इसमें अभाज्य संख्या $5$ नहीं है।

अंकगणित की आधारभूत प्रमेय की अद्वितीयता यह गारंटी देती है कि $2$ के अलावा इसका कोई और गुणनखंड नहीं हो सकता।

निष्कर्ष: अतः ऐसी कोई प्राकृत संख्या $n$ नहीं है जिसके लिए $4^n$ अंक $0$ पर समाप्त हो।

प्रश्न 3: घंटी बजने वाला प्रश्न (Word Problem on LCM)

प्रश्न: तीन घंटियां क्रमशः 4, 7 और 14 मिनट के अंतराल पर बजती हैं। यदि वे तीनों सुबह 6:00 बजे एक साथ बजी हों, तो वे दोबारा एक साथ कब बजेंगी? (UP Board 2022)

हल:

घंटियां दोबारा एक साथ तब बजेंगी, जब बीता हुआ समय 4, 7 और 14 का न्यूनतम समापवर्त्य (LCM) होगा।

$4 = 2^2$

$7 = 7^1$

$14 = 2 \times 7 = 2^1 \times 7^1$

$LCM =$ सबसे बड़ी घातों का गुणनफल $= 2^2 \times 7^1 = 4 \times 7 = 28$

निष्कर्ष: घंटियां 28 मिनट बाद पुनः एक साथ बजेंगी। अतः समय $= 6:00 + 28 \text{ मिनट} = \text{सुबह } 6:28 \text{ बजे}$ ।

प्रश्न 4: काजू बर्फी का प्रश्न (Word Problem on HCF)

प्रश्न: एक मिठाई विक्रेता के पास 420 काजू की बर्फियां और 130 बादाम की बर्फियां हैं। वह इनकी ऐसी ढेरियाँ बनाना चाहता है कि प्रत्येक ढेरी में बर्फियों की संख्या समान रहे और ये ढेरियाँ बर्फी की परात में न्यूनतम स्थान घेरें। एक ढेरी में कितनी बर्फियां रखी जा सकती हैं? (NCERT / MP Board)

हल:

परात में न्यूनतम स्थान घेरने के लिए, प्रत्येक ढेरी में बर्फियों की संख्या अधिकतम होनी चाहिए।

अधिकतम संख्या निकालने के लिए हमें $420$ और $130$ का HCF (महत्तम समापवर्तक) ज्ञात करना होगा।

$420 = 2^2 \times 3 \times 5 \times 7$

$130 = 2 \times 5 \times 13$

उभयनिष्ठ गुणनखंड $2$ और $5$ हैं। इनकी सबसे छोटी घात $2^1$ और $5^1$ है।

$HCF(420, 130) = 2 \times 5 = 10$

उत्तर: अतः प्रत्येक ढेरी में 10 बर्फियां रखी जा सकती हैं।

प्रश्न 5: सूत्र आधारित प्रश्न

प्रश्न: यदि दो संख्याओं का LCM $2079$ है और उनका HCF $27$ है। यदि उनमें से एक संख्या $189$ है, तो दूसरी संख्या ज्ञात कीजिए। (BSEB 2023)

हल:

हम जानते हैं:

$\text{पहली संख्या} \times \text{दूसरी संख्या} = HCF \times LCM<span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-933a4c78a0db535dc8df5e73d1be66df_l3.png" height="13" width="151" class="ql-img-displayed-equation " alt="\[$189 \times \text{दूसरी संख्या} = 27 \times 2079\]" title="Rendered by QuickLaTeX.com"/><span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-283b127bb15060cb466b230c4443e997_l3.png" height="37" width="96" class="ql-img-displayed-equation " alt="\[\text{दूसरी संख्या} = \frac{27 \times 2079}{189}\]" title="Rendered by QuickLaTeX.com"/>  $

27 $से$ 189

$सात (7) बार में कटता है:<span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-6d97f1867fe4d06c2abc5426a2ae6b4d_l3.png" height="37" width="109" class="ql-img-displayed-equation " alt="\[\text{दूसरी संख्या} = \frac{2079}{7} = 297\]" title="Rendered by QuickLaTeX.com"/>   <strong>उत्तर:</strong> दूसरी संख्या$

297

*** QuickLaTeX cannot compile formula:
है।
<!-- /wp:paragraph -->

<!-- wp:heading -->
<h2 class="wp-block-heading"><strong>5. Frequently Asked Questions (FAQs) - अक्सर पूछे जाने वाले प्रश्न</strong></h2>
<!-- /wp:heading -->

<!-- wp:rank-math/faq-block {"questions":[{"id":"faq-question-1781252160409","title":"\u003cstrong\u003eअंकगणित की आधारभूत प्रमेय का गणित में क्या महत्व है?\u003c/strong\u003e","content":"यह प्रमेय गणित का वह नियम है जो साबित करता है कि हर भाज्य संख्या का एक \u0022अद्वितीय DNA\u0022 (अभाज्य गुणनखंड) होता है। इसके बिना भिन्न (Fractions) को सरल करना, HCF, और LCM निकालना असंभव होता।","visible":true},{"id":"faq-question-1781252175880","title":"\u003cstrong\u003eWord Problems में यह कैसे पहचानें कि HCF निकालना है या LCM?\u003c/strong\u003e","content":"\u003cstrong\u003eHCF की पहचान:\u003c/strong\u003e जब प्रश्न में किसी चीज़ को \u0022समान और अधिकतम बड़े भागों में बाँटने\u0022, \u0022अधिकतम क्षमता\u0022, या \u0022न्यूनतम स्थान घेरने\u0022 (जिसका अर्थ अधिकतम स्टैक बनाना हो) की बात हो, तो HCF निकालें।\u003cbr\u003e\u003cstrong\u003eLCM की पहचान:\u003c/strong\u003e जब प्रश्न में \u0022घटनाएं एक साथ कब होंगी\u0022, \u0022न्यूनतम समय\u0022, \u0022एक ही बिंदु पर पुनः कब मिलेंगे\u0022 (जैसे दौड़ना, घंटियां बजना, ट्रैफिक लाइट बदलना) की बात हो, तो LCM निकालें।","visible":true},{"id":"faq-question-1781252217349","title":"\u003cstrong\u003eक्या \u003c/strong\u003e

*** Error message:
Unicode character ह (U+0939)
leading text: $ह
Unicode character ै (U+0948)
leading text: $है
Unicode character । (U+0964)
leading text: $है।
Missing $ inserted.
Unicode character अ (U+0905)
leading text: ...5. Frequently Asked Questions (FAQs) - अ
Unicode character क (U+0915)
leading text: ...Frequently Asked Questions (FAQs) - अक
Unicode character ् (U+094D)
leading text: ...quently Asked Questions (FAQs) - अक्
Unicode character स (U+0938)
leading text: ...ntly Asked Questions (FAQs) - अक्स
Unicode character र (U+0930)
leading text: ...y Asked Questions (FAQs) - अक्सर
Unicode character प (U+092A)
leading text: ...ked Questions (FAQs) - अक्सर प
Unicode character ू (U+0942)

1 $\u003cstrong\u003e एक अभाज्य (Prime) संख्या है?\u003c/strong\u003e","content":"नहीं,$ 1

*** QuickLaTeX cannot compile formula:
न तो अभाज्य संख्या है और न ही भाज्य संख्या है। यह एक विशिष्ट (Unique) संख्या है। अभाज्य संख्या की परिभाषा के अनुसार उसके ठीक दो गुणनखंड (

*** Error message:
Unicode character न (U+0928)
leading text: $न
Unicode character त (U+0924)
leading text: $न त
Unicode character ो (U+094B)
leading text: $न तो
Unicode character अ (U+0905)
leading text: $न तो अ
Unicode character भ (U+092D)
leading text: $न तो अभ
Unicode character ा (U+093E)
leading text: $न तो अभा
Unicode character ज (U+091C)
leading text: $न तो अभाज
Unicode character ् (U+094D)
leading text: $न तो अभाज्
Unicode character य (U+092F)
leading text: $न तो अभाज्य
Unicode character स (U+0938)
leading text: $न तो अभाज्य स
Unicode character ं (U+0902)
leading text: $न तो अभाज्य सं
Unicode character ख (U+0916)

1 $और वह स्वयं) होने चाहिए, जबकि$ 1 $का केवल एक ही गुणनखंड है।","visible":true},{"id":"faq-question-1781252233668","title":"\u003cstrong\u003eयदि दो संख्याओं का HCF \u003c/strong\u003e$ 1 $\u003cstrong\u003e हो, तो उन संख्याओं को क्या कहते हैं?\u003c/strong\u003e","content":"जिन दो संख्याओं का HCF$ 1 $होता है, उन्हें \u003cstrong\u003eसह-अभाज्य संख्याएं (Co-prime Numbers)\u003c/strong\u003e कहा जाता है। उदाहरण:$ 8 $और$ 15 $(दोनों भाज्य हैं, लेकिन इनमें$ 1 $के अलावा कोई कॉमन गुणनखंड नहीं है)।","visible":true},{"id":"faq-question-1781252250480","title":"\u003cstrong\u003eक्या \u003c/strong\u003e$ HCF \u005ctimes LCM = a \u005ctimes b \u005ctimes c

*** QuickLaTeX cannot compile formula:
\u003cstrong\u003e (तीन संख्याओं के लिए) सत्य है?\u003c/strong\u003e","content":"बिल्कुल नहीं! यह सूत्र केवल दो संख्याओं पर ही लागू होता है। तीन संख्याओं के लिए हमें अनिवार्य रूप से अभाज्य गुणनखंडन विधि का ही उपयोग करना ","visible":true}]} -->
<div class="wp-block-rank-math-faq-block"><div class="rank-math-faq-item"><h3 class="rank-math-question"><strong>अंकगणित की आधारभूत प्रमेय का गणित में क्या महत्व है?</strong></h3><div class="rank-math-answer">यह प्रमेय गणित का वह नियम है जो साबित करता है कि हर भाज्य संख्या का एक "अद्वितीय DNA" (अभाज्य गुणनखंड) होता है। इसके बिना भिन्न (Fractions) को सरल करना, HCF, और LCM निकालना असंभव होता।</div></div><div class="rank-math-faq-item"><h3 class="rank-math-question"><strong>Word Problems में यह कैसे पहचानें कि HCF निकालना है या LCM?</strong></h3><div class="rank-math-answer"><strong>HCF की पहचान:</strong> जब प्रश्न में किसी चीज़ को "समान और अधिकतम बड़े भागों में बाँटने", "अधिकतम क्षमता", या "न्यूनतम स्थान घेरने" (जिसका अर्थ अधिकतम स्टैक बनाना हो) की बात हो, तो HCF निकालें।<strong>LCM की पहचान:</strong> जब प्रश्न में "घटनाएं एक साथ कब होंगी", "न्यूनतम समय", "एक ही बिंदु पर पुनः कब मिलेंगे" (जैसे दौड़ना, घंटियां बजना, ट्रैफिक लाइट बदलना) की बात हो, तो LCM निकालें।</div></div><div class="rank-math-faq-item"><h3 class="rank-math-question"><strong>क्या </strong>

*** Error message:
Please use \mathaccent for accents in math mode.
leading text: $\u0
Please use \mathaccent for accents in math mode.
leading text: $\u003cstrong\u0
Unicode character त (U+0924)
leading text: $\u003cstrong\u003e (त
Unicode character ी (U+0940)
leading text: $\u003cstrong\u003e (ती
Unicode character न (U+0928)
leading text: $\u003cstrong\u003e (तीन
Unicode character स (U+0938)
leading text: $\u003cstrong\u003e (तीन स
Unicode character ं (U+0902)
leading text: $\u003cstrong\u003e (तीन सं
Unicode character ख (U+0916)
leading text: $\u003cstrong\u003e (तीन संख
Unicode character ् (U+094D)
leading text: $\u003cstrong\u003e (तीन संख्
Unicode character य (U+092F)
leading text: $\u003cstrong\u003e (तीन संख्य

1 $<strong> एक अभाज्य (Prime) संख्या है?</strong></h3><div class="rank-math-answer">नहीं,$ 1

*** QuickLaTeX cannot compile formula:
न तो अभाज्य संख्या है और न ही भाज्य संख्या है। यह एक विशिष्ट (Unique) संख्या है। अभाज्य संख्या की परिभाषा के अनुसार उसके ठीक दो गुणनखंड (

*** Error message:
Unicode character न (U+0928)
leading text: $न
Unicode character त (U+0924)
leading text: $न त
Unicode character ो (U+094B)
leading text: $न तो
Unicode character अ (U+0905)
leading text: $न तो अ
Unicode character भ (U+092D)
leading text: $न तो अभ
Unicode character ा (U+093E)
leading text: $न तो अभा
Unicode character ज (U+091C)
leading text: $न तो अभाज
Unicode character ् (U+094D)
leading text: $न तो अभाज्
Unicode character य (U+092F)
leading text: $न तो अभाज्य
Unicode character स (U+0938)
leading text: $न तो अभाज्य स
Unicode character ं (U+0902)
leading text: $न तो अभाज्य सं
Unicode character ख (U+0916)

1 $और वह स्वयं) होने चाहिए, जबकि$ 1 $का केवल एक ही गुणनखंड है।</div></div><div class="rank-math-faq-item"><h3 class="rank-math-question"><strong>यदि दो संख्याओं का HCF </strong>$ 1 $<strong> हो, तो उन संख्याओं को क्या कहते हैं?</strong></h3><div class="rank-math-answer">जिन दो संख्याओं का HCF$ 1 $होता है, उन्हें <strong>सह-अभाज्य संख्याएं (Co-prime Numbers)</strong> कहा जाता है। उदाहरण:$ 8 $और$ 15 $(दोनों भाज्य हैं, लेकिन इनमें$ 1 $के अलावा कोई कॉमन गुणनखंड नहीं है)।</div></div><div class="rank-math-faq-item"><h3 class="rank-math-question"><strong>क्या </strong>$ HCF \times LCM = a \times b \times c$ (तीन संख्याओं के लिए) सत्य है?

बिल्कुल नहीं! यह सूत्र केवल दो संख्याओं पर ही लागू होता है। तीन संख्याओं के लिए हमें अनिवार्य रूप से अभाज्य गुणनखंडन विधि का ही उपयोग करना

परिभाषा (Definition)

विस्तृत व्याख्या (Detailed Explanation)

उदाहरण (10th Maths Fundamental Theorem of Arithmetic)

उपयोग (Applications)

विशेष बिंदु (Key Points)

Useful for Lower Grade Students

1. अंकगणित की आधारभूत प्रमेय क्या है? (What is Fundamental Theorem of Arithmetic?)

1.1 प्रमेय का आधिकारिक कथन (Official Statement)

1.2 सरल शब्दों में व्याख्या (Simple Explanation)

2. अभाज्य गुणनखंडन के बेहतरीन उदाहरण (Extra Examples of Prime Factorization)

3. प्रमेय के मुख्य अनुप्रयोग (Important Applications of the Theorem)

A. HCF और LCM ज्ञात करना (Finding HCF & LCM)

B. संख्या के अंत में शून्य (0) आने की शर्त

C. भाज्य संख्या की जांच

4. Board Exam PYQs & Word Problems (पिछले वर्षों के सबसे महत्वपूर्ण प्रश्न)

प्रश्न 1: तीन संख्याओं का HCF और LCM (Basic Application)

प्रश्न 2: शून्य पर समाप्त होने वाली संख्या (Conceptual VVI)

प्रश्न 3: घंटी बजने वाला प्रश्न (Word Problem on LCM)

प्रश्न 4: काजू बर्फी का प्रश्न (Word Problem on HCF)

प्रश्न 5: सूत्र आधारित प्रश्न

Leave a Comment