MP Board Class 12 Physics Electric Field
1.6 विद्युत क्षेत्र (Electric Field)
1.6.1 परिचय (Introduction)
हम पहले ही कूलॉम के नियम से जान चुके हैं कि एक आवेशित कण दूसरे आवेशित कण पर बल लगाता है। प्रश्न यह उठता है कि यह बल बिना किसी सीधे संपर्क (direct contact) के, दूर से कैसे कार्य करता है? इस ‘दूर से क्रिया’ (action at a distance) की अवधारणा को समझाने के लिए, वैज्ञानिक माइकल फैराडे (Michael Faraday) ने विद्युत क्षेत्र (Electric Field) की अवधारणा प्रस्तुत की।
विद्युत क्षेत्र, आवेशों के चारों ओर का वह स्थान है जहाँ उनके वैद्युत प्रभाव को अनुभव किया जा सकता है। यह एक ऐसी राशि है जो आवेश के चारों ओर के अंतरिक्ष (space) की एक विशेषता बताती है, न कि केवल आवेशित वस्तुओं की अंतःक्रिया को।
1.6.2 विद्युत क्षेत्र की परिभाषा (Definition of Electric Field)
किसी आवेश या आवेशों के निकाय (system of charges) के चारों ओर का वह क्षेत्र जिसमें कोई अन्य परीक्षण आवेश (test charge) वैद्युत बल का अनुभव करता है, विद्युत क्षेत्र कहलाता है।
गणितीय रूप से, किसी बिंदु पर विद्युत क्षेत्र (E) को उस बिंदु पर रखे गए अत्यंत छोटे धनात्मक परीक्षण आवेश (q0) पर लगने वाले वैद्युत बल (F) और उस परीक्षण आवेश के परिमाण के अनुपात (ratio) के रूप में परिभाषित किया जाता है:
महत्वपूर्ण बिंदु:
- परीक्षण आवेश q0 बहुत छोटा होना चाहिए ताकि वह स्वयं मूल आवेश वितरण (source charge distribution) को प्रभावित न करे।
- विद्युत क्षेत्र एक सदिश राशि (vector quantity) है। इसकी दिशा वही होती है जो धनात्मक परीक्षण आवेश पर लगने वाले बल की दिशा होती है।
1.6.3 बिंदु आवेश के कारण विद्युत क्षेत्र (Electric Field Due to a Point Charge)
माना एक बिंदु आवेश Q मूल बिंदु (origin) पर स्थित है। इससे r दूरी पर स्थित किसी बिंदु P पर विद्युत क्षेत्र ज्ञात करना है। बिंदु P पर एक धनात्मक परीक्षण आवेश q0 रखते हैं।
कूलॉम के नियम के अनुसार, Q द्वारा q0 पर लगने वाला बल (F):F=4πϵ01r2Qq0r^
जहाँ r^ आवेश Q से बिंदु P की ओर एकांक सदिश है।
विद्युत क्षेत्र की परिभाषा से:E=q0F
मान रखने पर:E=q01(4πϵ01r2Qq0r^)
अतः, एक बिंदु आवेश Q के कारण r दूरी पर विद्युत क्षेत्र का सूत्र है:E=4πϵ01r2Qr^
दिशा:
- यदि Q धनात्मक है, तो E की दिशा आवेश Q से बाहर की ओर (radially outward) होगी।
- यदि Q ऋणात्मक है, तो E की दिशा आवेश Q की ओर (radially inward) होगी।
1.6.4 विद्युत क्षेत्र का मात्रक (Unit of Electric Field)
विद्युत क्षेत्र (E) का मात्रक बल (F) और आवेश (q) के मात्रकों से व्युत्पन्न होता है।
- बल का मात्रक = न्यूटन (N)
- आवेश का मात्रक = कूलॉम (C)
अतः, विद्युत क्षेत्र का SI मात्रक न्यूटन प्रति कूलॉम (Newton per Coulomb या N/C) है।
इसे वोल्ट प्रति मीटर (V/m) के रूप में भी व्यक्त किया जा सकता है, जिसके बारे में आप आगे के अध्यायों में सीखेंगे।
1.6.5 विद्युत क्षेत्र का भौतिक महत्व (Physical Significance of Electric Field)
- विद्युत क्षेत्र आवेशित वस्तुओं की अंतःक्रिया में एक मध्यवर्ती भूमिका निभाता है। जब कोई आवेश Q विद्युत क्षेत्र बनाता है, तो वह अपने चारों ओर अंतरिक्ष को “संशोधित” (modifies) कर देता है।
- जब कोई अन्य आवेश q0 इस क्षेत्र में लाया जाता है, तो वह इस संशोधित अंतरिक्ष के कारण बल का अनुभव करता है, न कि सीधे पहले आवेश Q से।
- यह अवधारणा ‘दूर से क्रिया’ की समस्या को हल करती है और हमें यह समझने में मदद करती है कि बल कैसे संचरित (propagated) होते हैं, यहाँ तक कि निर्वात में भी।
- विद्युत क्षेत्र एक वास्तविक भौतिक राशि है जो ऊर्जा धारण करती है और गति प्राप्त कर सकती है (विद्युतचुंबकीय तरंगों के रूप में)।
1.6.6 बहुल आवेशों के कारण विद्युत क्षेत्र (Electric Field Due to Multiple Charges)
यदि किसी निकाय में अनेक बिंदु आवेश q1,q2,q3,…,qn हों, तो किसी बिंदु पर कुल विद्युत क्षेत्र उन सभी आवेशों के कारण उत्पन्न अलग-अलग विद्युत क्षेत्रों के सदिश योग (vector sum) के बराबर होता है। इसे अध्यारोपण का सिद्धांत (Principle of Superposition) कहते हैं।
यदि किसी बिंदु पर q1 के कारण विद्युत क्षेत्र E1, q2 के कारण E2, और इसी प्रकार qn के कारण En हो, तो उस बिंदु पर कुल विद्युत क्षेत्र E होगा:E=E1+E2+E3+⋯+En
याE=i=1∑nEi=i=1∑n4πϵ01ri2qir^i
जहाँ ri आवेश qi से उस बिंदु की दूरी है, और r^i आवेश qi से उस बिंदु की ओर एकांक सदिश है।
परीक्षा के लिए महत्वपूर्ण बिंदु:
- विद्युत क्षेत्र की परिभाषा और सूत्र।
- बिंदु आवेश के कारण विद्युत क्षेत्र की दिशा।
- विद्युत क्षेत्र का SI मात्रक।
- अध्यारोपण का सिद्धांत।
- विद्युत क्षेत्र का भौतिक महत्व।
आवेशों के निकाय के कारण वैद्युत क्षेत्र: अध्यारोपण का सिद्धांत</h2>
(Electric Field Due to a System of Charges: Principle of Superposition)</h2>
1. परिचय (Introduction)
जब किसी अंतरिक्ष में एक से अधिक बिंदु आवेश (point charges) उपस्थित होते हैं, तो किसी दिए गए बिंदु पर कुल वैद्युत क्षेत्र (total electric field) कैसे ज्ञात किया जाए? इस समस्या को हल करने के लिए अध्यारोपण का सिद्धांत (Principle of Superposition) का उपयोग किया जाता है। यह सिद्धांत बताता है कि आवेशों के किसी निकाय (system of charges) के कारण किसी बिंदु पर कुल वैद्युत क्षेत्र, पृथक-पृथक आवेशों (individual charges) के कारण उस बिंदु पर उत्पन्न वैद्युत क्षेत्रों के सदिश योग के बराबर होता है।
2. आधारभूत अवधारणा (Basic Concept)
हमें पता है कि एक बिंदु आवेश 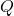 के कारण उससे
के कारण उससे  दूरी पर स्थित किसी बिंदु पर वैद्युत क्षेत्र
दूरी पर स्थित किसी बिंदु पर वैद्युत क्षेत्र 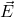 का मान निम्न सूत्र द्वारा दिया जाता है:
का मान निम्न सूत्र द्वारा दिया जाता है:
![Rendered by QuickLaTeX.com \[\vec{E} = \frac{1}{4\pi\epsilon_0} \frac{Q}{r^2} \hat{r}\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-67fe18583280d8951fb153781f6bb2c7_l3.png)
जहाँ 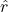 आवेश
आवेश 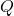 से उस बिंदु की ओर एकांक सदिश है।
3. गणितीय व्युत्पत्ति (Mathematical Derivation)
मान लीजिए हमारे पास
से उस बिंदु की ओर एकांक सदिश है।
3. गणितीय व्युत्पत्ति (Mathematical Derivation)
मान लीजिए हमारे पास  बिंदु आवेशों का एक निकाय है,
बिंदु आवेशों का एक निकाय है, 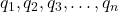 , जो अंतरिक्ष में विभिन्न बिंदुओं पर स्थित हैं। हमें किसी बिंदु
, जो अंतरिक्ष में विभिन्न बिंदुओं पर स्थित हैं। हमें किसी बिंदु  पर कुल वैद्युत क्षेत्र ज्ञात करना है।</p>
इस सिद्धांत को समझने के लिए, हम बिंदु
पर कुल वैद्युत क्षेत्र ज्ञात करना है।</p>
इस सिद्धांत को समझने के लिए, हम बिंदु  पर एक अत्यंत छोटा धनात्मक परीक्षण आवेश
पर एक अत्यंत छोटा धनात्मक परीक्षण आवेश  रखने की कल्पना करते हैं।
3.1. प्रत्येक आवेश द्वारा परीक्षण आवेश पर बल (Force on Test Charge by Each Individual Charge):
कूलॉम के नियम के अनुसार, प्रत्येक आवेश
रखने की कल्पना करते हैं।
3.1. प्रत्येक आवेश द्वारा परीक्षण आवेश पर बल (Force on Test Charge by Each Individual Charge):
कूलॉम के नियम के अनुसार, प्रत्येक आवेश 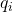 (जहाँ
(जहाँ 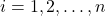 ) बिंदु
) बिंदु 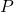 पर स्थित परीक्षण आवेश
पर स्थित परीक्षण आवेश 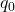 पर एक बल आरोपित करेगा।</p>
आवेश
पर एक बल आरोपित करेगा।</p>
आवेश 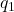 के कारण
के कारण 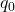 पर लगने वाला बल
पर लगने वाला बल 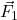 है। यदि
है। यदि 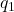 से
से 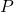 तक की दूरी
तक की दूरी 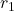 है, तो:
है, तो:
![Rendered by QuickLaTeX.com \[\vec{F}_1 = \frac{1}{4\pi\epsilon_0} \frac{q_1 q_0}{r_1^2} \hat{r}_1\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-d58ce9cb3b9219777ef4c7a10cf91039_l3.png)
जहाँ 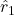 आवेश
आवेश 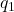 से बिंदु
से बिंदु 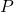 की ओर एकांक सदिश है।
इसी प्रकार, आवेश
की ओर एकांक सदिश है।
इसी प्रकार, आवेश 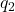 के कारण
के कारण 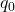 पर लगने वाला बल
पर लगने वाला बल 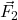 है। यदि
है। यदि 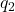 से
से 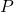 तक की दूरी
तक की दूरी 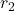 है, तो:
है, तो:
![Rendered by QuickLaTeX.com \[\vec{F}_2 = \frac{1}{4\pi\epsilon_0} \frac{q_2 q_0}{r_2^2} \hat{r}_2\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-a21512520e626ddfd0bdbf69cc33aada_l3.png)
और इसी प्रकार, आवेश 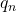 के कारण
के कारण 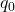 पर लगने वाला बल
पर लगने वाला बल 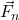 है। यदि
है। यदि 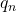 से
से 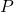 तक की दूरी
तक की दूरी  है, तो:
है, तो:
![Rendered by QuickLaTeX.com \[\vec{F}_n = \frac{1}{4\pi\epsilon_0} \frac{q_n q_0}{r_n^2} \hat{r}_n\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-7159cb932367dbe444e0b489f76210c9_l3.png)
3.2. कुल बल का अध्यारोपण (Superposition of Total Force):
अध्यारोपण के सिद्धांत के अनुसार, परीक्षण आवेश 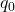 पर लगने वाला कुल बल
पर लगने वाला कुल बल 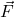 उन सभी अलग-अलग बलों का सदिश योग होता है:</p>
उन सभी अलग-अलग बलों का सदिश योग होता है:</p>
![Rendered by QuickLaTeX.com \[\vec{F}_{\text{कुल}} = \vec{F}_1 + \vec{F}_2 + \vec{F}_3 + \dots + \vec{F}_n\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-00ea3df0f1abb64459e0f437d70c2ce9_l3.png)
प्रत्येक 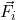 के लिए कूलॉम नियम के व्यंजक को प्रतिस्थापित करने पर:
के लिए कूलॉम नियम के व्यंजक को प्रतिस्थापित करने पर:
![Rendered by QuickLaTeX.com \[\vec{F}_{\text{कुल}} = \frac{1}{4\pi\epsilon_0} \frac{q_1 q_0}{r_1^2} \hat{r}_1 + \frac{1}{4\pi\epsilon_0} \frac{q_2 q_0}{r_2^2} \hat{r}_2 + \dots + \frac{1}{4\pi\epsilon_0} \frac{q_n q_0}{r_n^2} \hat{r}_n\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-03570d91158359e03bfc776787a4aae7_l3.png)
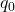 को उभयनिष्ठ (common) लेने पर:
को उभयनिष्ठ (common) लेने पर:
![Rendered by QuickLaTeX.com \[\vec{F}_{\text{कुल}} = q_0 \left[ \frac{1}{4\pi\epsilon_0} \frac{q_1}{r_1^2} \hat{r}_1 + \frac{1}{4\pi\epsilon_0} \frac{q_2}{r_2^2} \hat{r}_2 + \dots + \frac{1}{4\pi\epsilon_0} \frac{q_n}{r_n^2} \hat{r}_n \right]\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-445938a4e08e8845ec3f95c9215f80d8_l3.png)
3.3. कुल वैद्युत क्षेत्र का व्युत्पत्ति (Derivation of Total Electric Field):
<p>विद्युत क्षेत्र की परिभाषा के अनुसार, किसी बिंदु पर कुल वैद्युत क्षेत्र उस बिंदु पर लगने वाले कुल बल को परीक्षण आवेश के परिमाण से विभाजित करके प्राप्त किया जाता है:
![Rendered by QuickLaTeX.com \[\vec{E}_{\text{कुल}} = \frac{\vec{F}_{\text{कुल}}}{q_0}\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-f2df943290c27b61f034ce7481080c39_l3.png)
<p>उपरोक्त समीकरण में 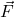 का मान रखने पर:</p>
का मान रखने पर:</p>
![Rendered by QuickLaTeX.com \[\vec{E}_{\text{कुल}} = \frac{1}{q_0} \left[ q_0 \left( \frac{1}{4\pi\epsilon_0} \frac{q_1}{r_1^2} \hat{r}_1 + \frac{1}{4\pi\epsilon_0} \frac{q_2}{r_2^2} \hat{r}_2 + \dots + \frac{1}{4\pi\epsilon_0} \frac{q_n}{r_n^2} \hat{r}_n \right) \right]\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-51ebad2c8cae5394162b079f5b1f1f7a_l3.png)
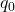 रद्द (cancel) हो जाता है:</p>
रद्द (cancel) हो जाता है:</p>
![Rendered by QuickLaTeX.com \[\vec{E}_{\text{कुल}} = \frac{1}{4\pi\epsilon_0} \frac{q_1}{r_1^2} \hat{r}_1 + \frac{1}{4\pi\epsilon_0} \frac{q_2}{r_2^2} \hat{r}_2 + \dots + \frac{1}{4\pi\epsilon_0} \frac{q_n}{r_n^2} \hat{r}_n\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-851ff44eaa920f1a45fed344ddda5815_l3.png)
चूँकि प्रत्येक पद 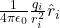 वास्तव में आवेश
वास्तव में आवेश 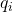 के कारण उस बिंदु पर उत्पन्न वैद्युत क्षेत्र
के कारण उस बिंदु पर उत्पन्न वैद्युत क्षेत्र 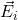 है, हम लिख सकते हैं:
है, हम लिख सकते हैं:
![Rendered by QuickLaTeX.com \[\vec{E}_{\text{कुल}} = \vec{E}_1 + \vec{E}_2 + \vec{E}_3 + \dots + \vec{E}_n\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-08bcee2d65e84ef65295de6947fa923e_l3.png)
<p>संक्षिप्त रूप में, योग चिह्न (summation notation) का उपयोग करते हुए:
![Rendered by QuickLaTeX.com \[\vec{E}_{\text{कुल}} = \sum_{i=1}^{n} \vec{E}_i\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-a6d616495f799794fa42198c40f3e07b_l3.png)
4. निष्कर्ष (Conclusion)</h3>
इस प्रकार, यह सिद्ध होता है कि <strong>आवेशों के निकाय के कारण किसी बिंदु पर कुल वैद्युत क्षेत्र, पृथक-पृथक आवेशों के कारण उस बिंदु पर उत्पन्न वैद्युत क्षेत्रों के सदिश योग के बराबर होता है।</strong> यह अध्यारोपण का सिद्धांत स्थिरवैद्युतिकी में जटिल आवेश वितरणों के कारण क्षेत्रों की गणना करने का एक शक्तिशाली उपकरण है।1.7.2 विद्युत क्षेत्र का भौतिक अभिप्राय (Physical Significance of Electric Field)
1. परिचय (Introduction)
आपको आश्चर्य हो सकता है कि हमें यहाँ विद्युत क्षेत्र की धारणा से परिचित क्यों कराया जा रहा है। आखिर, आवेशों के किसी भी निकाय के लिए किसी आवेश पर लगने वाला मापने योग्य बल तो कूलॉम नियम और अध्यारोपण सिद्धांत द्वारा सीधे ही निर्धारित किया जा सकता है। फिर विद्युत क्षेत्र नामक इस मध्यवर्ती राशि (intermediate quantity) को प्रस्तावित क्यों किया जा रहा है? इसकी वास्तविक भौतिक सार्थकता क्या है?
2. स्थिरवैद्युतिकी में विद्युत क्षेत्र (Electric Field in Electrostatics)
स्थिरवैद्युतिकी (Electrostatics) के संदर्भ में, विद्युत क्षेत्र की अवधारणा सुगम तो है, पर वास्तव में यह उतनी आवश्यक नहीं प्रतीत होती। इसे आवेशों के किसी निकाय के वैद्युत पर्यावरण (electrical environment) को दर्शाने का एक सुरुचि संपन्न (elegant) तरीका माना जा सकता है।
- वैद्युत पर्यावरण का अभिलक्षण: आवेशों के निकाय के चारों ओर के दिक्स्थान (space) में किसी बिंदु पर विद्युत क्षेत्र हमें यह बताता है कि यदि निकाय को बिना किसी विक्षोभ (disturbance) के उस बिंदु पर कोई एकांक धनात्मक परीक्षण आवेश (unit positive test charge) रखा जाए, तो वह कितना बल अनुभव करेगा।
- निकाय का अभिलक्षण: विद्युत क्षेत्र आवेशों के निकाय का एक विशिष्ट अभिलक्षण (characteristic) है। इसका निर्धारण आपके द्वारा उस बिंदु पर रखे जाने वाले परीक्षण आवेश पर निर्भर नहीं करता।
- सदिश राशि: चूंकि बल एक सदिश राशि है, अतः विद्युत क्षेत्र भी एक सदिश राशि है। भौतिकी में ‘क्षेत्र’ (field) शब्द का उपयोग व्यापक रूप से उस राशि को निर्दिष्ट करने के लिए किया जाता है, जो दिक्स्थान के प्रत्येक बिंदु पर परिभाषित की जा सके तथा एक बिंदु से दूसरे बिंदु पर परिवर्तित होती हो।
3. काल-आश्रित वैद्युतचुंबकीय परिघटनाओं में वास्तविक सार्थकता (Real Significance in Time-Dependent Electromagnetic Phenomena)
विद्युत क्षेत्र की अवधारणा की वास्तविक भौतिक सार्थकता (physical significance) तभी प्रकट होती है जब हम स्थिरवैद्युतिकी से बाहर निकलकर काल-आश्रित (time-dependent) वैद्युतचुंबकीय परिघटनाओं (electromagnetic phenomena) से व्यवहार करते हैं।
- काल विलंब (Time Delay): मान लीजिए हम त्वरित गति (accelerated motion) से गतिमान दो दूरस्थ आवेशों q1 तथा q2 के बीच लगने वाले बल पर विचार करते हैं। हमें पता है कि कोई भी संकेत (signal) या सूचना अधिकतम प्रकाश की चाल c से ही एक स्थान से दूसरे स्थान तक जा सकती है। इस प्रकार, q1 पर q2 की किसी गति का प्रभाव तात्क्षणिक (instantaneously) उत्पन्न नहीं हो सकता। कारण (q1 की गति) तथा प्रभाव (q2 पर बल) के बीच कुछ न कुछ काल विलंब (time delay) अवश्य होता है।
- क्षेत्र की भूमिका: यहीं पर विद्युत क्षेत्र (सही अर्थों में वैद्युतचुंबकीय क्षेत्र) की अवधारणा स्वाभाविक एवं अति उपयोगी है। क्षेत्र का चित्रण इस प्रकार है:
- आवेश q1 की त्वरित गति वैद्युतचुंबकीय तरंगें (electromagnetic waves) उत्पन्न करती है।
- ये तरंगें फिर प्रकाश की चाल से फैलकर q2 तक पहुँचती हैं।
- इसके परिणामस्वरूप q2 पर बल लगाती हैं।
- विलंब का स्पष्टीकरण: क्षेत्र की अवधारणा इस काल विलंब का सुचारु रूप से स्पष्टीकरण करती है।
4. क्षेत्र का भौतिक अस्तित्व (Physical Existence of Field)
यद्यपि वैद्युत तथा चुंबकीय बलों की संसूचना (detection) केवल आवेशों पर इनके प्रभावों (बलों) द्वारा ही की जा सकती है, उन्हें वास्तविक भौतिक सत्व (physical entities) माना जाता है; ये केवल गणितीय रचनाएँ ही नहीं हैं।
- स्वतंत्र गतिकी: इनकी अपनी स्वतंत्र गतिकी (independent dynamics) है, अर्थात् ये अपने नियमों के अनुसार विकसित होते हैं।
- ऊर्जा का परिवहन: ये ऊर्जा का परिवहन (transport energy) भी कर सकते हैं। इस प्रकार, काल-आश्रित वैद्युतचुंबकीय क्षेत्रों का कोई स्रोत, जिसे अल्प समय अंतराल के लिए खोलकर फिर बंद किया जा सकता है, ऊर्जा परिवहन करने वाले वैद्युतचुंबकीय क्षेत्रों को पीछे छोड़ देता है।
5. फैराडे का योगदान और निष्कर्ष (Faraday’s Contribution and Conclusion)
क्षेत्र की अवधारणा सर्वप्रथम फैराडे ने प्रस्तावित की थी जो भौतिकी की प्रमुख अवधारणाओं में स्थान रखती है। यह अवधारणा आधुनिक भौतिकी, विशेषकर विद्युतचुंबकीय तरंगों (जैसे प्रकाश) और क्वांटम क्षेत्र सिद्धांत (Quantum Field Theory) की नींव है।
संक्षेप में, विद्युत क्षेत्र न केवल आवेशों के चारों ओर के पर्यावरण का वर्णन करता है, बल्कि यह बलों के संचरण और ऊर्जा के परिवहन में एक वास्तविक मध्यस्थ के रूप में भी कार्य करता है।