कूलॉम का नियम (Coulomb’s Law) विद्युत-स्थैतिकी का एक मूलभूत सिद्धांत है, जो दो बिंदु आवेशों के बीच लगने वाले बल का मात्रात्मक विवरण देता है। यह नियम चार्ल्स-ऑगस्टिन डी कूलॉम द्वारा 18वीं शताब्दी में प्रतिपादित किया गया था। यह नियम बताता है कि दो आवेशित कणों के बीच का बल उनके आवेशों के परिमाणों के गुणनफल के समानुपाती और उनके बीच की दूरी के वर्ग के व्युत्क्रमानुपाती होता है। यह बल आवेशों को जोड़ने वाली रेखा के अनुदिश कार्य करता है।
कूलॉम का नियम
जब दो आवेशित वस्तुओं का आकार उनकी बीच की दूरी की तुलना में बहुत छोटा हो, तो उन्हें बिंदु आवेश माना जा सकता है। कूलॉम का नियम गणितीय रूप में निम्नलिखित है:
![]()
जहाँ:
F :दो आवेशों के बीच लगने वाला बल (न्यूटन में)
q_1, q_2 : दो बिंदु आवेशों की मात्रा (कूलॉम में)
r : दो आवेशों के बीच की दूरी (मीटर में)
k : कूलॉम स्थिरांक, जिसका मान निर्वात में लगभग ![]() है
है
बल की प्रकृति
यदि ![]() और
और ![]() समान चिह्न (दोनों धनात्मक या दोनों ऋणात्मक) के हैं, तो बल प्रतिकर्षी होता है।
समान चिह्न (दोनों धनात्मक या दोनों ऋणात्मक) के हैं, तो बल प्रतिकर्षी होता है।
\item यदि ![]() और
और ![]() विपरीत चिह्न (एक धनात्मक और एक ऋणात्मक) के हैं, तो बल आकर्षक होता है।
विपरीत चिह्न (एक धनात्मक और एक ऋणात्मक) के हैं, तो बल आकर्षक होता है।
{कूलॉम नियम का सदिश रूप}
बल एक सदिश राशि है, इसलिए कूलॉम नियम को सदिश रूप में व्यक्त करना अधिक उपयुक्त है। माना कि ![]() और
और ![]() दो बिंदु आवेश हैं, जिनके स्थिति सदिश क्रमशः
दो बिंदु आवेश हैं, जिनके स्थिति सदिश क्रमशः ![]() और
और ![]() हैं। इनके बीच की सापेक्ष दूरी
हैं। इनके बीच की सापेक्ष दूरी ![]() है। बल
है। बल ![]() (जो
(जो ![]() पर
पर ![]() द्वारा लगता है) निम्नलिखित रूप में व्यक्त होता है:
द्वारा लगता है) निम्नलिखित रूप में व्यक्त होता है:
![]()
जहाँ:
![]() :
: ![]() से
से ![]() की ओर इंगित करने वाला एकांक सदिश
की ओर इंगित करने वाला एकांक सदिश
![]() : निर्वात की विद्युतशीलता, जिसका मान
: निर्वात की विद्युतशीलता, जिसका मान ![]()
![]()
इसी प्रकार, ![]() पर
पर ![]() द्वारा लगने वाला बल:
द्वारा लगने वाला बल:
![]()
यह न्यूटन के तृतीय नियम (![]() ) के अनुरूप है।
) के अनुरूप है।
कूलॉम के प्रयोग
कूलॉम ने अपने नियम की खोज के लिए ऐंठन तुला (Torsion Balance) का उपयोग किया। उनके प्रयोगों में निम्नलिखित प्रक्रिया अपनाई गई:
{प्रयोग की प्रक्रिया}
कूलॉम ने दो धातु के गोलों का उपयोग किया, जिनका आकार उनके बीच की दूरी की तुलना में बहुत छोटा था, ताकि उन्हें बिंदु आवेश माना जा सके।
प्रारंभ में, गोलों पर आवेश की मात्रा अज्ञात थी। कूलॉम ने एक चतुर विधि अपनाई: एक आवेशित गोले (![]() ) को एक अनावेशित गोले के संपर्क में लाने पर, आवेश समान रूप से दोनों गोलों में बंट जाता है, जिससे प्रत्येक पर
) को एक अनावेशित गोले के संपर्क में लाने पर, आवेश समान रूप से दोनों गोलों में बंट जाता है, जिससे प्रत्येक पर ![]() आवेश प्राप्त होता है।
आवेश प्राप्त होता है।
इस प्रक्रिया को दोहराकर, ![]() आदि आवेश प्राप्त किए गए।
आदि आवेश प्राप्त किए गए।
कूलॉम ने विभिन्न आवेश युगलों और दूरियों के लिए बल को मापा। पहले, उन्होंने एक निश्चित आवेश युगल के लिए दूरी बदलकर बल मापा, फिर दूरी को स्थिर रखकर आवेशों को बदला।
इन मापों की तुलना करके, कूलॉम ने पाया कि बल ![]() के समानुपाती और
के समानुपाती और ![]() के व्युत्क्रमानुपाती है, जिससे समीकरण
के व्युत्क्रमानुपाती है, जिससे समीकरण ![]() प्राप्त हुआ।
प्राप्त हुआ।
प्रयोगों का महत्व
कूलॉम के प्रयोगों ने न केवल स्थूल स्तर पर, बल्कि अवपरमाणुक स्तर (![]() ) तक इस नियम की पुष्टि की। यह नियम सरल गणितीय रूप में होने के बावजूद अत्यंत शक्तिशाली है और विद्युत-स्थैतिकी के अध्ययन का आधार है।
) तक इस नियम की पुष्टि की। यह नियम सरल गणितीय रूप में होने के बावजूद अत्यंत शक्तिशाली है और विद्युत-स्थैतिकी के अध्ययन का आधार है।
{कूलॉम की परिभाषा}
कूलॉम का नियम आवेश के मात्रक को परिभाषित करने में भी उपयोगी है। यदि ![]() और
और ![]() , तो:
, तो:
![]()
अर्थात, 1 कूलॉम वह आवेश है जो निर्वात में 1 मीटर दूरी पर रखे समान परिमाण के किसी अन्य आवेश को ![]() न्यूटन बल से प्रतिकर्षित करता है। व्यावहारिक उपयोग में, 1 कूलॉम बहुत बड़ा मात्रक है, इसलिए सूक्ष्म-कूलॉम (
न्यूटन बल से प्रतिकर्षित करता है। व्यावहारिक उपयोग में, 1 कूलॉम बहुत बड़ा मात्रक है, इसलिए सूक्ष्म-कूलॉम (![]() ) और मिली-कूलॉम (
) और मिली-कूलॉम (![]() ) का उपयोग किया जाता है।
) का उपयोग किया जाता है।
{अनुप्रयोग}
कूलॉम का नियम निम्नलिखित क्षेत्रों में उपयोगी है:
विद्युत क्षेत्र की गणना
कणों के बीच पारस्परिक क्रिया का अध्ययन
इलेक्ट्रॉनिक्स और इंजीनियरिंग में डिज़ाइन
परमाणु और आणविक संरचनाओं का विश्लेषण
निष्कर्ष
कूलॉम का नियम विद्युत-स्थैतिकी का एक आधारभूत सिद्धांत है, जो आवेशित कणों के बीच बल को समझने में महत्वपूर्ण है। कूलॉम के प्रयोगों ने इस नियम को स्थूल और सूक्ष्म दोनों स्तरों पर स्थापित किया। यह नियम न केवल सैद्धांतिक भौतिकी में, बल्कि व्यावहारिक अनुप्रयोगों में भी महत्वपूर्ण भूमिका निभाता है।
उदाहरण 1.3: स्थिरवैद्युत तथा गुरुत्वाकर्षण बल की तुलना
प्रश्न:दो वैद्युत आवेशों के बीच स्थिर वैद्युत बल के लिए कूलॉम नियम तथा दो स्थिर बिंदु द्रव्यमानों के बीच गुरुत्वाकर्षण बल के लिए न्यूटन का नियम दोनों में ही बल आवेशों/द्रव्यमानों के बीच की दूरी के वर्ग के व्युत्क्रमानुपाती होता है।
- इन दोनों बलों के परिमाण ज्ञात करके इनकी प्रबलताओं की तुलना की जाए:
- एक इलेक्ट्रॉन तथा एक प्रोटॉन के लिए।
- दो प्रोटॉनों के लिए।
- इलेक्ट्रॉन तथा प्रोटॉन में पारस्परिक आकर्षण के वैद्युत बल के कारण इलेक्ट्रॉन तथा प्रोटॉन के त्वरण आकलित कीजिए जबकि इनके बीच की दूरी
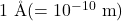 है।
है।
दिए गए मान:
- प्रोटॉन का द्रव्यमान (
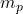 ) =
) = 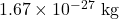
- इलेक्ट्रॉन का द्रव्यमान (
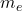 ) =
) = 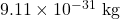
- इलेक्ट्रॉन/प्रोटॉन का आवेश (
 ) =
) = 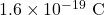
- गुरुत्वाकर्षण नियतांक (
 ) =
) = 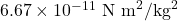
- कूलॉम नियतांक (
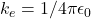 ) =
) = 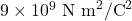
हल:
दूरी 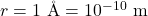
(a) बलों के परिमाणों की तुलना
(i) एक इलेक्ट्रॉन तथा एक प्रोटॉन के लिए (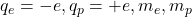 ):
):
स्थिर वैद्युत बल (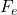 ):
):
![Rendered by QuickLaTeX.com \[F_e = k_e \frac{|q_e q_p|}{r^2} = k_e \frac{e^2}{r^2}\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-6ac77473088e3d0d1d334fba2bb9b5c5_l3.png)
![Rendered by QuickLaTeX.com \[F_e = (9 \times 10^9 \text{ N m}^2/\text{C}^2) \times \frac{(1.6 \times 10^{-19} \text{ C})^2}{(10^{-10} \text{ m})^2}\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-6f652c4e04734152efb6cedd54b230b7_l3.png)
![Rendered by QuickLaTeX.com \[F_e = 9 \times 10^9 \times \frac{2.56 \times 10^{-38}}{10^{-20}} \text{ N}\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-456678193a00a05395491255fdf2fa1b_l3.png)
![Rendered by QuickLaTeX.com \[F_e = 9 \times 2.56 \times 10^{(9-38+20)} \text{ N}\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-3ddbd6595be8f09e5f3d55c5f5ee21dd_l3.png)
![Rendered by QuickLaTeX.com \[F_e = 23.04 \times 10^{-9} \text{ N} = 2.304 \times 10^{-8} \text{ N}\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-f820fa49f30da3e3b774584da5d7c417_l3.png)
गुरुत्वाकर्षण बल (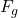 ):
):
![Rendered by QuickLaTeX.com \[F_g = G \frac{m_e m_p}{r^2}\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-cf90c8d48f43f0b6b7ed320a796e35d7_l3.png)
![Rendered by QuickLaTeX.com \[F_g = (6.67 \times 10^{-11} \text{ N m}^2/\text{kg}^2) \times \frac{(9.11 \times 10^{-31} \text{ kg}) \times (1.67 \times 10^{-27} \text{ kg})}{(10^{-10} \text{ m})^2}\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-6630be0dd171259a44f642b10a528c9f_l3.png)
![Rendered by QuickLaTeX.com \[F_g = 6.67 \times 10^{-11} \times \frac{15.22 \times 10^{-58}}{10^{-20}} \text{ N}\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-fff93e57e6b79e0430db009e8167a1fd_l3.png)
![Rendered by QuickLaTeX.com \[F_g = 6.67 \times 15.22 \times 10^{(-11-58+20)} \text{ N}\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-097b68cfaa48a1d1bd598107d8179c25_l3.png)
![Rendered by QuickLaTeX.com \[F_g \approx 101.5 \times 10^{-49} \text{ N} = 1.015 \times 10^{-47} \text{ N}\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-ebc194ed588df55bd91b134298123db4_l3.png)
बलों की प्रबलता की तुलना:
![Rendered by QuickLaTeX.com \[\frac{F_e}{F_g} = \frac{2.304 \times 10^{-8} \text{ N}}{1.015 \times 10^{-47} \text{ N}}\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-97ffb1f8f743b230660ea30c5bf3ec32_l3.png)
![Rendered by QuickLaTeX.com \[\frac{F_e}{F_g} \approx 2.27 \times 10^{39}\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-6cb57d6c345901c2a6bb1b549dd20e2e_l3.png)
यह दर्शाता है कि एक इलेक्ट्रॉन और एक प्रोटॉन के बीच स्थिर वैद्युत बल गुरुत्वाकर्षण बल की तुलना में लगभग 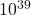 गुना अधिक प्रबल होता है।
गुना अधिक प्रबल होता है।
(ii) दो प्रोटॉनों के लिए (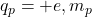 ):
):
स्थिर वैद्युत बल (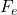 ):
):
![Rendered by QuickLaTeX.com \[F_e = k_e \frac{|q_p q_p|}{r^2} = k_e \frac{e^2}{r^2}\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-7924157f17afee6a7eb4a87f7183d841_l3.png)
![Rendered by QuickLaTeX.com \[F_e = (9 \times 10^9 \text{ N m}^2/\text{C}^2) \times \frac{(1.6 \times 10^{-19} \text{ C})^2}{(10^{-10} \text{ m})^2}\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-6f652c4e04734152efb6cedd54b230b7_l3.png)
![Rendered by QuickLaTeX.com \[F_e = 2.304 \times 10^{-8} \text{ N}\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-ea30765e6fbd23e4451526e357818089_l3.png)
(यह मान इलेक्ट्रॉन-प्रोटॉन के प्रकरण के समान है क्योंकि आवेश का परिमाण समान है।)
गुरुत्वाकर्षण बल (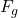 ):
):
![Rendered by QuickLaTeX.com \[F_g = G \frac{m_p m_p}{r^2} = G \frac{m_p^2}{r^2}\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-f3842d5b4af536d532d6704d25c7997a_l3.png)
![Rendered by QuickLaTeX.com \[F_g = (6.67 \times 10^{-11} \text{ N m}^2/\text{kg}^2) \times \frac{(1.67 \times 10^{-27} \text{ kg})^2}{(10^{-10} \text{ m})^2}\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-80d79a51dd9cec92211b7b27b3ebd540_l3.png)
![Rendered by QuickLaTeX.com \[F_g = 6.67 \times 10^{-11} \times \frac{2.789 \times 10^{-54}}{10^{-20}} \text{ N}\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-1121c7a24d0cf62aed0469c888587f2d_l3.png)
![Rendered by QuickLaTeX.com \[F_g = 6.67 \times 2.789 \times 10^{(-11-54+20)} \text{ N}\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-a94dbbadeb69dc210bbdefc9318826fc_l3.png)
![Rendered by QuickLaTeX.com \[F_g \approx 18.59 \times 10^{-45} \text{ N} = 1.859 \times 10^{-44} \text{ N}\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-96bd52767bf388834a7a482e374c7953_l3.png)
बलों की प्रबलता की तुलना:
![Rendered by QuickLaTeX.com \[\frac{F_e}{F_g} = \frac{2.304 \times 10^{-8} \text{ N}}{1.859 \times 10^{-44} \text{ N}}\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-ca5811e5ab1bf160587b7483d4037e1f_l3.png)
![Rendered by QuickLaTeX.com \[\frac{F_e}{F_g} \approx 1.239 \times 10^{36}\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-2e76f750376b6469faaeeabc7c88981f_l3.png)
यह दर्शाता है कि दो प्रोटॉनों के बीच स्थिर वैद्युत बल गुरुत्वाकर्षण बल की तुलना में **लगभग 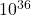 गुना अधिक प्रबल** होता है।
गुना अधिक प्रबल** होता है।
(b) इलेक्ट्रॉन तथा प्रोटॉन के त्वरण आकलित कीजिए
इलेक्ट्रॉन तथा प्रोटॉन के बीच लगने वाला स्थिर वैद्युत आकर्षण बल  (भाग a(i) से)।
(भाग a(i) से)।
न्यूटन के द्वितीय नियम (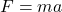 ) से त्वरण (
) से त्वरण (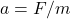 ) ज्ञात करते हैं:
) ज्ञात करते हैं:
इलेक्ट्रॉन का त्वरण (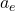 ):
):
![Rendered by QuickLaTeX.com \[a_e = \frac{F_e}{m_e}\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-52571ea494ec8633fe0d396c19c29892_l3.png)
![Rendered by QuickLaTeX.com \[a_e = \frac{2.304 \times 10^{-8} \text{ N}}{9.11 \times 10^{-31} \text{ kg}}\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-1dba6f5b88e4cc34bcaad37ff341cd7d_l3.png)
![Rendered by QuickLaTeX.com \[a_e \approx 0.2529 \times 10^{(-8+31)} \text{ m/s}^2\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-4bb7de2c1bf226af60b1ec575ae1eae7_l3.png)
![Rendered by QuickLaTeX.com \[a_e \approx 2.53 \times 10^{22} \text{ m/s}^2\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-7285f1e16cc28cae02c5d87690dd665c_l3.png)
प्रोटॉन का त्वरण (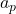 ):
):
![Rendered by QuickLaTeX.com \[a_p = \frac{F_e}{m_p}\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-d768d82af564a8498701b12445dec89f_l3.png)
![Rendered by QuickLaTeX.com \[a_p = \frac{2.304 \times 10^{-8} \text{ N}}{1.67 \times 10^{-27} \text{ kg}}\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-9d216f64bf3156721d37bcf58a53bb38_l3.png)
![Rendered by QuickLaTeX.com \[a_p \approx 1.380 \times 10^{(-8+27)} \text{ m/s}^2\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-b9c30d4361edab4f0e73f9d85b49d6b9_l3.png)
![Rendered by QuickLaTeX.com \[a_p \approx 1.38 \times 10^{19} \text{ m/s}^2\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-05676e6a779222faae686ae966811de4_l3.png)
निष्कर्ष: इलेक्ट्रॉन का त्वरण प्रोटॉन की तुलना में बहुत अधिक होता है क्योंकि इलेक्ट्रॉन का द्रव्यमान प्रोटॉन के द्रव्यमान से काफी कम होता है।
प्रश्न:दो वैद्युत आवेशों के बीच स्थिर वैद्युत बल के लिए कूलॉम नियम तथा दो स्थिर बिंदु द्रव्यमानों के बीच गुरुत्वाकर्षण बल के लिए न्यूटन का नियम दोनों में ही बल आवेशों/द्रव्यमानों के बीच की दूरी के वर्ग के व्युत्क्रमानुपाती होता है।
- इन दोनों बलों के परिमाण ज्ञात करके इनकी प्रबलताओं की तुलना की जाए:
- एक इलेक्ट्रॉन तथा एक प्रोटॉन के लिए।
- दो प्रोटॉनों के लिए।
- इलेक्ट्रॉन तथा प्रोटॉन में पारस्परिक आकर्षण के वैद्युत बल के कारण इलेक्ट्रॉन तथा प्रोटॉन के त्वरण आकलित कीजिए जबकि इनके बीच की दूरी
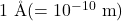 है।
है।
- एक इलेक्ट्रॉन तथा एक प्रोटॉन के लिए।
- दो प्रोटॉनों के लिए।
दिए गए मान:
- प्रोटॉन का द्रव्यमान (
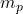 ) =
) = 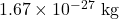
- इलेक्ट्रॉन का द्रव्यमान (
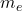 ) =
) = 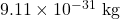
- इलेक्ट्रॉन/प्रोटॉन का आवेश (
 ) =
) = 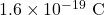
- गुरुत्वाकर्षण नियतांक (
 ) =
) = 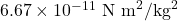
- कूलॉम नियतांक (
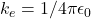 ) =
) = 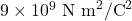
दूरी ![]()
(a) बलों के परिमाणों की तुलना
(i) एक इलेक्ट्रॉन तथा एक प्रोटॉन के लिए (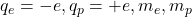 ):
):
स्थिर वैद्युत बल (![]() ):
):
![]()
![]()
![]()
![]()
![]()
गुरुत्वाकर्षण बल (![]() ):
):
![]()
![]()
![]()
![]()
![]()
बलों की प्रबलता की तुलना:
![]()
![]()
यह दर्शाता है कि एक इलेक्ट्रॉन और एक प्रोटॉन के बीच स्थिर वैद्युत बल गुरुत्वाकर्षण बल की तुलना में लगभग ![]() गुना अधिक प्रबल होता है।
गुना अधिक प्रबल होता है।
(ii) दो प्रोटॉनों के लिए (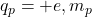 ):
):
स्थिर वैद्युत बल (![]() ):
):
![]()
![]()
![]()
(यह मान इलेक्ट्रॉन-प्रोटॉन के प्रकरण के समान है क्योंकि आवेश का परिमाण समान है।)
गुरुत्वाकर्षण बल (![]() ):
):
![]()
![]()
![]()
![]()
![]()
बलों की प्रबलता की तुलना:
![]()
![]()
यह दर्शाता है कि दो प्रोटॉनों के बीच स्थिर वैद्युत बल गुरुत्वाकर्षण बल की तुलना में **लगभग ![]() गुना अधिक प्रबल** होता है।
गुना अधिक प्रबल** होता है।
(b) इलेक्ट्रॉन तथा प्रोटॉन के त्वरण आकलित कीजिए
इलेक्ट्रॉन तथा प्रोटॉन के बीच लगने वाला स्थिर वैद्युत आकर्षण बल ![]() (भाग a(i) से)।
(भाग a(i) से)।
न्यूटन के द्वितीय नियम (![]() ) से त्वरण (
) से त्वरण (![]() ) ज्ञात करते हैं:
) ज्ञात करते हैं:
इलेक्ट्रॉन का त्वरण (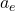 ):
):
![]()
![]()
![]()
![]()
प्रोटॉन का त्वरण (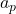 ):
):
![]()
![]()
![]()
![]()
निष्कर्ष: इलेक्ट्रॉन का त्वरण प्रोटॉन की तुलना में बहुत अधिक होता है क्योंकि इलेक्ट्रॉन का द्रव्यमान प्रोटॉन के द्रव्यमान से काफी कम होता है।