MP Board 9th Real numbers and their decimal expansions
MP Board 9th Real numbers and their decimal expansions : इस अनुच्छेद में, हम एक अलग दृष्टिकोण से परिमेय और अपरिमेय संख्याओं का अध्ययन करेंगे। इसके लिए हम वास्तविक संख्याओं के दशमलव प्रसार (expansions) पर विचार करेंगे और देखेंगे कि क्या हम परिमेय संख्याओं और अपरिमेय संख्याओं में भेद करने के लिए इन प्रसारों का प्रयोग कर सकते हैं या नहीं। यहाँ हम इस बात की भी व्याख्या करेंगे कि वास्तविक संख्याओं के दशमलव प्रसार का प्रयोग करके किस प्रकार1 संख्या रेखा पर वास्तविक संख्याओं को प्रदर्शित किया जाता है। क्योंकि हम अपरिमेय संख्याओं की तुलना में परिमेय संख्याओं से अधिक परिचित हैं, इसलिए हम अपनी चर्चा इन्हीं संख्याओं से आरंभ करेंगे। यहाँ इनके तीन उदाहरण दिए गए हैं : ![]() ,
, ![]() ,
, ![]() । शेषफलों पर विशेष ध्यान दीजिए और देखिए कि क्या आप कोई प्रतिरूप (pattern) प्राप्त कर सकते हैं।
। शेषफलों पर विशेष ध्यान दीजिए और देखिए कि क्या आप कोई प्रतिरूप (pattern) प्राप्त कर सकते हैं।
उदाहरण 5 ![]() ,
, ![]() और
और ![]() के दशमलव प्रसार ज्ञात कीजिए।
के दशमलव प्रसार ज्ञात कीजिए।
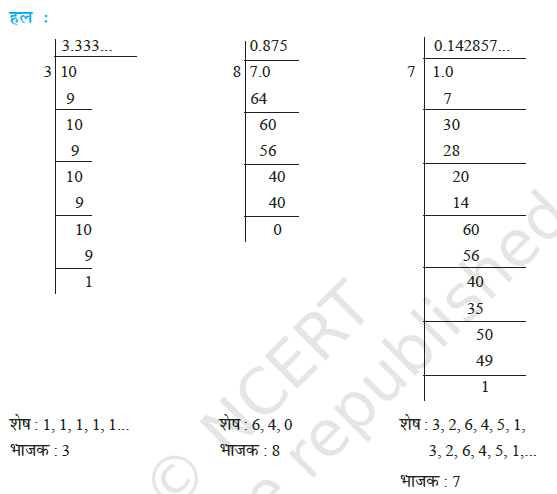
यद्यपि केवल ऊपर दिए गए उदाहरणों से हमने यह प्रतिरूप प्राप्त किया है, परन्तु यह ![]()
![]() के रूप की सभी परिमेय संख्याओं पर लागू होता है।
के रूप की सभी परिमेय संख्याओं पर लागू होता है। ![]() से
से ![]() को भाग देने पर दो मुख्य बातें घटित होती हैं – या तो शेष शून्य हो जाता है या कभी भी शून्य नहीं होता है और तब हमें शेषफलों की एक पुनरावृत्ति श्रृंखला प्राप्त होती है। आइए हम प्रत्येक स्थिति पर अलग-अलग विचार करें।
को भाग देने पर दो मुख्य बातें घटित होती हैं – या तो शेष शून्य हो जाता है या कभी भी शून्य नहीं होता है और तब हमें शेषफलों की एक पुनरावृत्ति श्रृंखला प्राप्त होती है। आइए हम प्रत्येक स्थिति पर अलग-अलग विचार करें।
स्थिति (i) : शेष शून्य हो जाता है।
![]() वाले उदाहरण में हमने यह देखा है कि कुछ चरणों के बाद शेष शून्य हो जाता है और
वाले उदाहरण में हमने यह देखा है कि कुछ चरणों के बाद शेष शून्य हो जाता है और ![]() का दशमलव प्रसार
का दशमलव प्रसार ![]() है। अन्य उदाहरण हैं :
है। अन्य उदाहरण हैं : ![]() ,
, ![]() । इन सभी स्थितियों में कुछ परिमित चरणों के बाद दशमलव प्रसार का अंत हो जाता है। हम ऐसी संख्याओं के दशमलव प्रसार को सांत (terminating) दशमलव कहते हैं।
। इन सभी स्थितियों में कुछ परिमित चरणों के बाद दशमलव प्रसार का अंत हो जाता है। हम ऐसी संख्याओं के दशमलव प्रसार को सांत (terminating) दशमलव कहते हैं।
यहाँ आपने किन-किन बातों पर ध्यान दिया है? आपको कम से कम तीन बातों पर ध्यान देना चाहिए।
(i) कुछ चरण के बाद शेष या तो 0 हो जाते हैं या स्वयं की पुनरावृत्ति करना प्रारंभ कर देते हैं।
(ii) शेषों की पुनरावृत्ति श्रृंखला में प्रविष्टियों (entries) की संख्या भाजक से कम होती है (31 में एक संख्या की पुनरावृत्ति होती है और भाजक 3 है, 71 में शेषों की पुनरावृत्ति श्रृंखला में छ: प्रविष्टियाँ 326451 हैं और भाजक 7 है)।
(iii) यदि शेषों की पुनरावृत्ति होती है, तो भागफल (quotient) में अंकों का एक पुनरावृत्ति खंड प्राप्त होता है (31 के लिए भागफल में 3 की पुनरावृत्ति होती है और 71 के लिए भागफल में पुनरावृत्ति खंड 142857 प्राप्त होता है)।
स्थिति (ii) : शेष कभी भी शून्य नहीं होता है।
![]() और
और ![]() वाले उदाहरणों में, हम यह पाते हैं कि कुछ चरणों के बाद शेष की पुनरावृत्ति होने लगती है, जिससे दशमलव प्रसार निरंतर जारी रहता है। दूसरे शब्दों में, हमें भागफल में अंकों का एक पुनरावृत्ति खंड प्राप्त होता है। तब हम यह कहते हैं कि यह प्रसार अनवसानी आवर्ती (non-terminating recurring) है। उदाहरण के लिए,
वाले उदाहरणों में, हम यह पाते हैं कि कुछ चरणों के बाद शेष की पुनरावृत्ति होने लगती है, जिससे दशमलव प्रसार निरंतर जारी रहता है। दूसरे शब्दों में, हमें भागफल में अंकों का एक पुनरावृत्ति खंड प्राप्त होता है। तब हम यह कहते हैं कि यह प्रसार अनवसानी आवर्ती (non-terminating recurring) है। उदाहरण के लिए, ![]() और
और ![]() है।
है।
यह दिखाने के लिए कि ![]() के भागफल में
के भागफल में ![]() की पुनरावृत्ति होती है, हम इसे
की पुनरावृत्ति होती है, हम इसे ![]() के रूप में लिखते हैं। इसी प्रकार, क्योंकि
के रूप में लिखते हैं। इसी प्रकार, क्योंकि ![]() के भागफल में अंकों के खंड
के भागफल में अंकों के खंड ![]() की पुनरावृत्ति होती है, इसलिए हम
की पुनरावृत्ति होती है, इसलिए हम ![]() को
को ![]() के रूप में लिखते हैं, जहाँ अंकों के ऊपर लगाया गया दंड, अंकों के उस खंड को प्रकट करता है जिसकी पुनरावृत्ति होती है। साथ ही,
के रूप में लिखते हैं, जहाँ अंकों के ऊपर लगाया गया दंड, अंकों के उस खंड को प्रकट करता है जिसकी पुनरावृत्ति होती है। साथ ही, ![]() को
को ![]() के रूप में लिखा जा सकता है। अतः: इन सभी उदाहरणों से अनवसानी आवर्त (पुनरावृत्ति) दशमलव प्रसार प्राप्त होते हैं। इस तरह हम यह देखते हैं कि परिमेय संख्याओं के दशमलव प्रसार के केवल दो विकल्प होते हैं या तो वे सांत होते हैं या अनवसानी (असांत) आवर्ती होते हैं।
के रूप में लिखा जा सकता है। अतः: इन सभी उदाहरणों से अनवसानी आवर्त (पुनरावृत्ति) दशमलव प्रसार प्राप्त होते हैं। इस तरह हम यह देखते हैं कि परिमेय संख्याओं के दशमलव प्रसार के केवल दो विकल्प होते हैं या तो वे सांत होते हैं या अनवसानी (असांत) आवर्ती होते हैं।
इसके विपरीत अब आप यह मान लीजिए कि संख्या रेखा पर चलने पर आपको 3.142678 जैसी संख्याएँ प्राप्त होती है जिसका दशमलव प्रसार सांत होता है या 1.272727…, अर्थात् ![]() जैसी संख्या प्राप्त होती है, जिसका दशमलव प्रसार अनवसानी आवर्ती है। इससे क्या आप यह निष्कर्ष निकाल सकते हैं कि यह एक परिमेय संख्या है? इसका उत्तर है, हाँ! इसे हम सिद्ध नहीं करेंगे, परन्तु कुछ उदाहरण लेकर इस तथ्य को प्रदर्शित करेंगे। सांत स्थितियाँ तो सरल हैं।
जैसी संख्या प्राप्त होती है, जिसका दशमलव प्रसार अनवसानी आवर्ती है। इससे क्या आप यह निष्कर्ष निकाल सकते हैं कि यह एक परिमेय संख्या है? इसका उत्तर है, हाँ! इसे हम सिद्ध नहीं करेंगे, परन्तु कुछ उदाहरण लेकर इस तथ्य को प्रदर्शित करेंगे। सांत स्थितियाँ तो सरल हैं।
उदाहरण 6 : दिखाइए कि 3.142678 एक परिमेय संख्या है। दूसरे शब्दों, में 3.142678 को ![]() के रूप में व्यक्त कीजिए, जहाँ
के रूप में व्यक्त कीजिए, जहाँ ![]() और
और ![]() पूर्णांक हैं और
पूर्णांक हैं और ![]() है।
है।
हल : यहाँ ![]() है। अतः यह एक परिमेय संख्या है।
है। अतः यह एक परिमेय संख्या है।
आइए अब हम उस स्थिति पर विचार करें, जबकि दशमलव प्रसार अनवसानी आवर्ती हो।
उदाहरण 7 : दिखाइए कि ![]() को
को ![]() के रूप में व्यक्त किया जा सकता है, जहाँ
के रूप में व्यक्त किया जा सकता है, जहाँ ![]() और
और ![]() पूर्णांक है और
पूर्णांक है और ![]() है।
है।
हल : क्योंकि हम यह नहीं जानते है कि 0.3 क्या है, अतः आइए इसे हम ‘x’ मान लो।
x=0.3333…
अब, यही वह स्थिति है जहाँ हमें कुछ युक्ति लगानी पड़ेगी।
यहाँ, 10x=10×(0.3333…)=3.333…
अब, 3.333…=3+x, चूँकि x=0.3333… है।
इसलिए, 10x=3+x
x के लिए हल करने पर, हमें यह प्राप्त होता है;
9x=3
अर्थात्, x=31
उदाहरण 8 : दिखाइए कि ![]() को
को ![]() के रूप में व्यक्त किया जा सकता है, जहाँ
के रूप में व्यक्त किया जा सकता है, जहाँ ![]() और
और ![]() पूर्णांक है और
पूर्णांक है और ![]() है।
है।
हल : मान लीजिए x=1.272727… है। क्योंकि यहाँ दो अंकों की पुनरावृत्ति है, इसलिए हम x को 100 से गुणा करते हैं। ऐसा करने पर, हमें यह प्राप्त होता है :
100x=127.2727…
अतः, ![]()
इसलिए, ![]() , अर्थात्
, अर्थात् ![]()
अर्थात्, ![]()
आप इसके इस विलोम की जाँच कर सकते है कि ![]() है।
है।
अब हम यह जानते हैं कि परिमेय संख्या का दशमलव प्रसार क्या हो सकता है। अब प्रश्न उठता है कि अपरिमेय संख्याओं का दशमलव प्रसार क्या होता है? ऊपर बताए गए गुण के अनुसार हम यह निष्कर्ष निकाल सकते हैं कि इन संख्याओं के दशमलव प्रसार अनवसानी अनावर्ती (non-terminating non-recurring) हैं। अतः ऊपर परिमेय संख्याओं के लिए बताए गए गुण के समान अपरिमेय संख्याओं का गुण यह होता है:
एक अपरिमेय संख्या का दशमलव प्रसार अनवसानी अनावर्ती होता है। विलोमतः वह संख्या जिसका दशमलव प्रसार अनवसानी अनावर्ती होता है, अपरिमेय होती है।1
पिछले अनुच्छेद में हमने एक अपरिमेय संख्या 0.10110111011110… की चर्चा की थी। मान लीजिए कि 2![]() है। ध्यान दीजिए कि यह अनवसानी अनावर्ती है। अतः ऊपर बताए गए गुण के अनुसार यह अपरिमेय है। साथ ही, यह भी ध्यान दीजिए कि आप s के समरूप अपरिमित रूप से अनेक अपरिमेय संख्याएँ जनित कर सकते हैं।3
है। ध्यान दीजिए कि यह अनवसानी अनावर्ती है। अतः ऊपर बताए गए गुण के अनुसार यह अपरिमेय है। साथ ही, यह भी ध्यान दीजिए कि आप s के समरूप अपरिमित रूप से अनेक अपरिमेय संख्याएँ जनित कर सकते हैं।3
सुप्रसिद्ध अपरिमेय संख्याओं4 ![]() और
और ![]() के संबंध में आप क्या जानते हैं? यहाँ कुछ चरण तक उनके दशमलव प्रसार दिए गए है:
के संबंध में आप क्या जानते हैं? यहाँ कुछ चरण तक उनके दशमलव प्रसार दिए गए है:
2=1.4142135623730950488016887242096…
π=3.14159265358979323846264338327950…
(ध्यान दीजिए कि हम प्रायः ![]() को
को ![]() का एक सन्निकट मान मानते है, जबकि
का एक सन्निकट मान मानते है, जबकि ![]() है।)
है।)
उदाहरण 9 : दिखाइए कि ![]() को
को ![]() के रूप में व्यक्त कर सकते हैं, जहाँ
के रूप में व्यक्त कर सकते हैं, जहाँ ![]() और
और ![]() पूर्णांक है और
पूर्णांक है और ![]() है।
है।
हल : मान लीजिए ![]() है। यहाँ यह देखिए कि 2 की पुनरावृत्ति नहीं होती है, परन्तु खंड 35 की पुनरावृत्ति होती है। क्योंकि दो अंकों की पुनरावृत्ति हो रही है, इसलिए हम
है। यहाँ यह देखिए कि 2 की पुनरावृत्ति नहीं होती है, परन्तु खंड 35 की पुनरावृत्ति होती है। क्योंकि दो अंकों की पुनरावृत्ति हो रही है, इसलिए हम ![]() को 100 से गुणा करते है। ऐसा करने पर, हमें यह प्राप्त होता है :
को 100 से गुणा करते है। ऐसा करने पर, हमें यह प्राप्त होता है :
![]()
इसलिए, ![]()
अतः, ![]()
अर्थात्, ![]() , जिससे
, जिससे ![]() हुआ।
हुआ।
आप इसके विलोम, अर्थात् ![]() की भी जाँच कर सकते हैं।
की भी जाँच कर सकते हैं।
अतः अनवसानी आवर्ती दशमलव प्रसार वाली प्रत्येक संख्या को ![]() (
(![]() ) के रूप में व्यक्त किया जा सकता है, जहाँ
) के रूप में व्यक्त किया जा सकता है, जहाँ ![]() और
और ![]() पूर्णांक है। आइए हम अपने परिणामों को संक्षेप में इस प्रकार व्यक्त करें:
पूर्णांक है। आइए हम अपने परिणामों को संक्षेप में इस प्रकार व्यक्त करें:
एक परिमेय संख्या का दशमलव प्रसार या तो सांत होता है या अनवसानी आवर्ती होता है। साथ ही, वह संख्या, जिसका दशमलव प्रसार सांत या अनवसानी आवर्ती है, एक परिमेय संख्या होती है।
अब हम यह जानते हैं कि परिमेय संख्या का दशमलव प्रसार क्या हो सकता है। अब प्रश्न उठता है कि अपरिमेय संख्याओं का दशमलव प्रसार क्या होता है? ऊपर बताए गए गुण के अनुसार हम यह निष्कर्ष निकाल सकते हैं कि इन संख्याओं के दशमलव प्रसार अनवसानी अनावर्ती (non-terminating non-recurring) हैं। अतः ऊपर परिमेय संख्याओं के लिए बताए गए गुण के समान अपरिमेय संख्याओं का गुण यह होता है:
एक अपरिमेय संख्या का दशमलव प्रसार अनवसानी अनावर्ती होता है। विलोमतः वह संख्या जिसका दशमलव प्रसार अनवसानी अनावर्ती होता है, अपरिमेय होती है।1
पिछले अनुच्छेद में हमने एक अपरिमेय संख्या 0.10110111011110… की चर्चा की थी। मान लीजिए कि 2![]() है। ध्यान दीजिए कि यह अनवसानी अनावर्ती है। अतः ऊपर बताए गए गुण के अनुसार यह अपरिमेय है। साथ ही, यह भी ध्यान दीजिए कि आप s के समरूप अपरिमित रूप से अनेक अपरिमेय संख्याएँ जनित कर सकते हैं।3
है। ध्यान दीजिए कि यह अनवसानी अनावर्ती है। अतः ऊपर बताए गए गुण के अनुसार यह अपरिमेय है। साथ ही, यह भी ध्यान दीजिए कि आप s के समरूप अपरिमित रूप से अनेक अपरिमेय संख्याएँ जनित कर सकते हैं।3
सुप्रसिद्ध अपरिमेय संख्याओं4 ![]() और
और ![]() के संबंध में आप क्या जानते हैं? यहाँ कुछ चरण तक उनके दशमलव प्रसार दिए गए है:
के संबंध में आप क्या जानते हैं? यहाँ कुछ चरण तक उनके दशमलव प्रसार दिए गए है:
2=1.4142135623730950488016887242096…
π=3.14159265358979323846264338327950…
(ध्यान दीजिए कि हम प्रायः ![]() को
को ![]() का एक सन्निकट मान मानते हैं, जबकि
का एक सन्निकट मान मानते हैं, जबकि ![]() है।)
है।)
वर्षों से गणितज्ञों ने अपरिमेय संख्याओं के दशमलव प्रसार में अधिक से अधिक अंकों को उत्पन्न करने की विभिन्न तकनीक विकसित की हैं। उदाहरण के लिए, संभवतः आपने विभाजन विधि (division method) से ![]() के दशमलव प्रसार में अंकों को ज्ञात करना अवश्य ही सीखा होगा। यह एक रोचक बात है कि सुल्बसूत्रों (जीवा-नियमों) में, जो वैदिक युग (800 ई.पू. – 500 ई.पू.) के गणितीय ग्रंथ हैं, हमें
के दशमलव प्रसार में अंकों को ज्ञात करना अवश्य ही सीखा होगा। यह एक रोचक बात है कि सुल्बसूत्रों (जीवा-नियमों) में, जो वैदिक युग (800 ई.पू. – 500 ई.पू.) के गणितीय ग्रंथ हैं, हमें ![]() का एक सन्निकट मान प्राप्त होता है, जो यह है:
का एक सन्निकट मान प्राप्त होता है, जो यह है:
![]()
ध्यान दीजिए कि यह वही है जो कि ऊपर प्रथम पाँच दशमलव स्थानों तक के लिए दिया गया है। ![]() के दशमलव प्रसार में अधिक से अधिक अंक प्राप्त करने का इतिहास काफी रोचक रहा है।
के दशमलव प्रसार में अधिक से अधिक अंक प्राप्त करने का इतिहास काफी रोचक रहा है।
ज़रूर, यहाँ आर्किमिडीज़ और पाई की उनकी गणना पर एक लेख हिंदी में है।
आर्किमिडीज़ और पाई (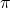 ) की गणना
) की गणना
प्राचीन काल के कई प्रतिभाशाली दिमागों में से, सिरैक्यूज़ के यूनानी गणितज्ञ आर्किमिडीज़ अपनी अविश्वसनीय प्रतिभा और सरलता के लिए सबसे अलग माने जाते हैं। उनकी कई महान उपलब्धियों में से, एक सबसे प्रसिद्ध उपलब्धि है गणितीय स्थिरांक पाई (![]() ) की उनकी आश्चर्यजनक रूप से सटीक गणना।
) की उनकी आश्चर्यजनक रूप से सटीक गणना।
कैलकुलेटर और कंप्यूटर के आविष्कार से बहुत पहले, आर्किमिडीज़ ने पाई का अनुमान लगाने के लिए एक क्रांतिकारी तरीका खोजा था, जिसे “निःशेषण विधि” (method of exhaustion) के रूप में जाना जाता है। उनके इस दृष्टिकोण की प्रतिभा इसकी सुंदर सादगी में निहित थी। उन्होंने यह समझा कि वे एक वृत्त की परिधि का अनुमान उसे दो बहुभुजों के बीच रखकर लगा सकते हैं।
आर्किमिडीज़ ने एक वृत्त के अंदर एक नियमित षट्भुज (hexagon) और उसी वृत्त के चारों ओर एक और षट्भुज बनाकर शुरुआत की। वे जानते थे कि वृत्त की परिधि, अंदर बने षट्भुज की परिधि से अधिक और बाहर बने षट्भुज की परिधि से कम होनी चाहिए।
इसके बाद, उन्होंने बहुभुजों की भुजाओं की संख्या को लगातार दोगुना किया — 6 से 12, फिर 24, 48, और अंत में, 96 भुजाओं वाले बहुभुज तक। भुजाओं की संख्या में प्रत्येक वृद्धि के साथ, अंदर और बाहर बने बहुभुजों की परिधि वृत्त की वास्तविक परिधि के और करीब आती गई। इससे पाई का मान एक संकीर्ण सीमा के अंदर सीमित होता गया।
इस सावधानीपूर्वक प्रक्रिया के माध्यम से, आर्किमिडीज़ यह साबित करने में सक्षम हुए कि पाई का मान 3 10/71 से अधिक और 3 1/7 से कम था। आधुनिक दशमलव प्रणाली में, यह पाई को लगभग 3.1408 और 3.1429 के बीच रखता है। यह गणित के इतिहास में एक बहुत बड़ी उपलब्धि थी, जिसने एक हजार से अधिक वर्षों तक पाई का सबसे सटीक अनुमान प्रदान किया।
उदाहरण 10 : ![]() और
और ![]() के बीच की एक अपरिमेय संख्या ज्ञात कीजिए।
के बीच की एक अपरिमेय संख्या ज्ञात कीजिए।
हल : हमने देखा है कि ![]() है।
है।
अतः, हम सरलता से यह परिकलित कर सकते हैं कि ![]() है।
है।
![]() और
और ![]() के बीच की एक अपरिमेय संख्या ज्ञात करने के लिए, हम एक ऐसी संख्या ज्ञात करते हैं जो इन दोनों के बीच स्थित अनवसानी अनावर्ती होती है। इस प्रकार की आप अपरिमेय रूप से अनेक संख्याएँ ज्ञात कर सकते हैं। इस प्रकार की संख्या का एक उदाहरण
के बीच की एक अपरिमेय संख्या ज्ञात करने के लिए, हम एक ऐसी संख्या ज्ञात करते हैं जो इन दोनों के बीच स्थित अनवसानी अनावर्ती होती है। इस प्रकार की आप अपरिमेय रूप से अनेक संख्याएँ ज्ञात कर सकते हैं। इस प्रकार की संख्या का एक उदाहरण ![]() है।
है।
नमस्ते! जैसा आपने कहा, मैं आपको प्रश्न ![]() का हल बिना किसी तालिका के, उचित चरणों के साथ हिंदी में प्रदान कर रहा हूँ।
का हल बिना किसी तालिका के, उचित चरणों के साथ हिंदी में प्रदान कर रहा हूँ।
प्रश्न यह है कि निम्नलिखित भिन्नों को दशमलव रूप में लिखिए और बताइए कि प्रत्येक का दशमलव प्रसार किस प्रकार का है (![]() या
या ![]() ):
):
1. भिन्नों का दशमलव प्रसार
(i) 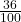
![]()
दशमलव प्रसार का प्रकार: यह एक सांत (Terminating) दशमलव प्रसार है क्योंकि भागफल एक निश्चित अंक के बाद समाप्त हो जाता है (शेषफल शून्य है)।
(ii) 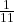
![]() को
को ![]() से भाग देने पर:
से भाग देने पर:
![Rendered by QuickLaTeX.com \[\begin{array}{r} 0.0909 \dots \\ 11 \overline{\smash) 1.0000} \\ \underline{-0} \\ 10 \\ \underline{-0} \\ 100 \\ \underline{-99} \\ 10 \\ \underline{-0} \\ 100 \\ \underline{-99} \\ 1 \end{array}\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-e753af1614950bc84ea6161430c30226_l3.png)
![]()
दशमलव प्रसार का प्रकार: यह एक अनवसानी आवर्ती (Non-terminating Repeating) दशमलव प्रसार है क्योंकि भाग की प्रक्रिया समाप्त नहीं होती है, लेकिन अंकों का एक समूह (09) बार-बार दोहराया जाता है।
(iii) 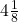
मिश्रित भिन्न को हल करने पर:
![]()
हम 81 का दशमलव रूप ज्ञात करते हैं: 81=0.125
अतः,
![]()
दशमलव प्रसार का प्रकार: यह एक सांत (Terminating) दशमलव प्रसार है।
(iv) 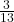
![]() को
को ![]() से भाग देने पर:
से भाग देने पर:
![Rendered by QuickLaTeX.com \[\begin{array}{r} 0.23076923 \dots \\ 13 \overline{\smash) 3.00000000} \\ \underline{-26} \\ 40 \\ \underline{-39} \\ 10 \\ \underline{-0} \\ 100 \\ \underline{-91} \\ 90 \\ \underline{-78} \\ 120 \\ \underline{-117} \\ 30 \leftarrow \text{यहां से शेषफल दोहराना शुरू होगा} \end{array}\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-2b802491b14b1a76717cc8fe2505b7ac_l3.png)
![]()
दशमलव प्रसार का प्रकार: यह एक अनवसानी आवर्ती (Non-terminating Repeating) दशमलव प्रसार है क्योंकि अंकों का समूह (230769) बार-बार दोहराया जाता है।
(v) 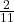
2 को 11 से भाग देने पर या 111 के परिणाम का उपयोग करने पर:
![]()
या भाग देने पर:
![]()
दशमलव प्रसार का प्रकार: यह एक अनवसानी आवर्ती (Non-terminating Repeating) दशमलव प्रसार है क्योंकि अंक (18) बार-बार दोहराया जाता है।
(vi) 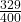
![]()
दशमलव प्रसार का प्रकार: यह एक सांत (![]() ) दशमलव प्रसार है।
) दशमलव प्रसार है।
जी! यह रहा प्रश्न 2 का हल ![]() , जिसमें लंबा भाग दिए बिना
, जिसमें लंबा भाग दिए बिना ![]() , और
, और ![]() के दशमलव प्रसार ज्ञात किए गए हैं।
के दशमलव प्रसार ज्ञात किए गए हैं।
2. लंबा भाग दिए बिना दशमलव प्रसार ज्ञात करना
दिया गया है:
![]()
उत्तर: हाँ, हम लंबा भाग दिए बिना दशमलव प्रसार ज्ञात कर सकते हैं।
कैसे?
71 का दशमलव प्रसार अनवसानी आवर्ती है, जिसका आवर्त खंड (Repeating Block) 142857 है। जब हम 1 को 7 से भाग देते हैं, तो शेषफल (1,3,2,6,4,5) एक निश्चित क्रम में आते हैं, और प्रत्येक शेषफल अगले अंक को निर्धारित करता है।
![]() का दशमलव प्रसार,
का दशमलव प्रसार, ![]() के अंकों (
के अंकों (![]() ) का चक्रीय क्रम (
) का चक्रीय क्रम (![]() ) होगा, जिसकी शुरुआत वह अंक करेगा जो
) होगा, जिसकी शुरुआत वह अंक करेगा जो ![]() के भाग में शेषफल
के भाग में शेषफल ![]() के बाद आया था।
के बाद आया था।
![]() के भाग से शेषफल और अगले अंक का क्रम:
के भाग से शेषफल और अगले अंक का क्रम:
![Rendered by QuickLaTeX.com \[\begin{array}{c|c} \text{शेषफल} & \text{अगला अंक (जहाँ से नया चक्र शुरू होगा)} \\ \hline 1 & \mathbf{1} \\ 3 & \mathbf{4} \\ 2 & \mathbf{2} \\ 6 & \mathbf{8} \\ 4 & \mathbf{5} \\ 5 & \mathbf{7} \\ \end{array}\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-b9bc4741a9195087ab421b40ec9123b8_l3.png)
(चूँकि ![]() है, इसलिए यह विभाजन
है, इसलिए यह विभाजन ![]() से शुरू होगा, जो
से शुरू होगा, जो ![]() के भाग में शेषफल
के भाग में शेषफल ![]() आने के बाद प्राप्त हुआ था)।
आने के बाद प्राप्त हुआ था)।
दशमलव प्रसार
प्रत्येक भिन्न के लिए, हम ![]() के अंकों के समूह को उसी अंक से शुरू करते हुए लिखेंगे जो शेषफल
के अंकों के समूह को उसी अंक से शुरू करते हुए लिखेंगे जो शेषफल ![]() के संगत है:
के संगत है:
- 72
(यह शेषफल 2 के संगत अंक 2 से शुरू होता है)![Rendered by QuickLaTeX.com \[\frac{2}{7} = 2 \times \frac{1}{7} = 2 \times \overline{0.142857} = \overline{0.\mathbf{285714}}\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-f66ae131850b9a25d71eede96448c897_l3.png)
- 73
(यह शेषफल 3 के संगत अंक 4 से शुरू होता है)![Rendered by QuickLaTeX.com \[\frac{3}{7} = 3 \times \frac{1}{7} = 3 \times \overline{0.142857} = \overline{0.\mathbf{428571}}\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-fe4c6c014ad62e6874f75da77d83fd06_l3.png)
- 74
(यह शेषफल 4 के संगत अंक 5 से शुरू होता है)![Rendered by QuickLaTeX.com \[\frac{4}{7} = 4 \times \frac{1}{7} = 4 \times \overline{0.142857} = \overline{0.\mathbf{571428}}\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-dbd1d48fda4004bf4a3eaadcfb43ab5f_l3.png)
- 75
(यह शेषफल 5 के संगत अंक 7 से शुरू होता है)![Rendered by QuickLaTeX.com \[\frac{5}{7} = 5 \times \frac{1}{7} = 5 \times \overline{0.142857} = \overline{0.\mathbf{714285}}\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-1cf8393df82cf21d5bea2996c849d820_l3.png)
- 76
(यह शेषफल 6 के संगत अंक 8 से शुरू होता है)![Rendered by QuickLaTeX.com \[\frac{6}{7} = 6 \times \frac{1}{7} = 6 \times \overline{0.142857} = \overline{0.\mathbf{857142}}\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-a23aa9b7725c6ec52e1c0c5672295a93_l3.png)
सभी भिन्नों का दशमलव प्रसार अनवसानी आवर्ती है, और सभी में अंकों का समूह ![]() ही चक्रीय क्रम में प्रयोग होता है।
ही चक्रीय क्रम में प्रयोग होता है।
जी! यह रहे आपके द्वारा दिए गए प्रश्नावली के प्रश्नों ![]() से
से ![]() तक के हल।
तक के हल।
3. निम्नलिखित को  के रूप में व्यक्त कीजिए।
के रूप में व्यक्त कीजिए।
(i) 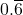
मान लीजिए x=0.6=0.666… (समीकरण 1)
चूँकि केवल एक अंक की पुनरावृत्ति हो रही है, इसलिए दोनों पक्षों को 10 से गुणा करने पर:
![]()
समीकरण (2) में से समीकरण (1) को घटाने पर:
![]()
![]()
![]()
![]()
उत्तर: 0.6=32
(ii) 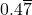
मान लीजिए x=0.47=0.4777… (समीकरण 1)
सबसे पहले, दशमलव को आवर्त खंड (7) के ठीक पहले लाने के लिए 10 से गुणा करने पर:
![]()
चूँकि आवर्त खंड में केवल एक अंक है, इसलिए समीकरण (2) को 10 से गुणा करने पर:
![]()
समीकरण (3) में से समीकरण (2) को घटाने पर:
![]()
![]()
![]()
उत्तर: 0.47=9043
(iii) 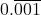
मान लीजिए x=0.001=0.001001001… (समीकरण 1)
चूँकि तीन अंकों (001) की पुनरावृत्ति हो रही है, इसलिए दोनों पक्षों को 1000 से गुणा करने पर:
![]()
समीकरण (2) में से समीकरण (1) को घटाने पर:
![]()
![]()
![]()
उत्तर: 0.001=9991
4. 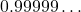 को
को  के रूप में व्यक्त कीजिए।
के रूप में व्यक्त कीजिए।
मान लीजिए x=0.99999… (समीकरण 1)
दोनों पक्षों को 10 से गुणा करने पर:
![]()
समीकरण (2) में से समीकरण (1) को घटाने पर:
![]()
![]()
![]()
![]()
उत्तर: 0.99999⋯=1
क्या आप अपने उत्तर से आश्चर्यचकित हैं? हाँ, यह उत्तर आश्चर्यजनक है क्योंकि 0.99999… देखने में 1 से थोड़ा कम लगता है, लेकिन गणितीय रूप से यह बिल्कुल 1 के बराबर है। इसका कारण यह है कि 0.99999… और 1 के बीच कोई अंतर नहीं है।
5.  के दशमलव प्रसार में अंकों के पुनरावृत्ति खंड में अंकों की अधिकतम संख्या क्या हो सकती है?
के दशमलव प्रसार में अंकों के पुनरावृत्ति खंड में अंकों की अधिकतम संख्या क्या हो सकती है?
जब किसी परिमेय संख्या qp (q=0) को दशमलव में बदला जाता है, तो अंकों के पुनरावृत्ति खंड में अंकों की संख्या भाजक (q) से हमेशा कम होती है।
यहाँ q=17 है।
अतः, 171 के दशमलव प्रसार में अंकों के पुनरावृत्ति खंड में अंकों की अधिकतम संख्या 17−1=16 हो सकती है।
उत्तर की जाँच करने के लिए विभाजन-क्रिया:
1 को 17 से भाग देने पर, हमें निम्नलिखित 16 अंकों का पुनरावृत्ति खंड मिलता है:
![]()
चूँकि अंकों की संख्या 16 है, हमारा उत्तर सही है।
6.  के रूप की परिमेय संख्याओं के अनेक उदाहरण
के रूप की परिमेय संख्याओं के अनेक उदाहरण
q के लिए वह गुण जिसे वह अवश्य संतुष्ट करना चाहिए, वह यह है कि q के अभाज्य गुणनखंड (Prime Factors) केवल 2 या 5 या दोनों होने चाहिए।
यदि q के अभाज्य गुणनखंड में 2 और 5 के अतिरिक्त कोई अन्य संख्या (जैसे 3,7,11) आती है, तो दशमलव प्रसार सांत (Terminating) नहीं होगा, बल्कि अनवसानी आवर्ती (Non-terminating Repeating) होगा।
उदाहरण:
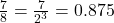 (यहाँ
(यहाँ 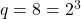 )
)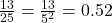 (यहाँ
(यहाँ 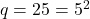 )
)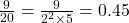 (यहाँ
(यहाँ 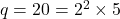 )
)
अनुमान: ![]() का अभाज्य गुणनखंडन (
का अभाज्य गुणनखंडन (![]() को
को ![]() और
और ![]() के सह-अभाज्य होने पर)
के सह-अभाज्य होने पर) ![]() के रूप में होना चाहिए, जहाँ
के रूप में होना चाहिए, जहाँ ![]() और
और ![]() ऋणेतर पूर्णांक (
ऋणेतर पूर्णांक (![]() ) हैं।
) हैं।
7. ऐसी तीन संख्याएँ लिखिए जिनके दशमलव प्रसार अनवसानी अनावर्ती हों।
अनवसानी अनावर्ती (![]() ) दशमलव प्रसार वाली संख्याएँ अपरिमेय संख्याएँ (
) दशमलव प्रसार वाली संख्याएँ अपरिमेय संख्याएँ (![]() ) कहलाती हैं।
) कहलाती हैं।
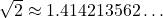
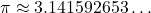
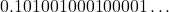 (यहाँ अंकों का कोई खंड दोहराया नहीं जाता)
(यहाँ अंकों का कोई खंड दोहराया नहीं जाता)
8. परिमेय संख्याओं  और
और  के बीच की तीन अलग-अलग अपरिमेय संख्याएँ ज्ञात कीजिए।
के बीच की तीन अलग-अलग अपरिमेय संख्याएँ ज्ञात कीजिए।
पहले इन परिमेय संख्याओं के दशमलव प्रसार ज्ञात करें:
अब हमें ![]() और
और ![]() के बीच तीन ऐसी संख्याएँ लिखनी हैं जो
के बीच तीन ऐसी संख्याएँ लिखनी हैं जो ![]() हों (अर्थात अपरिमेय हों)।
हों (अर्थात अपरिमेय हों)।
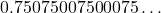
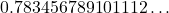 (याद रखें कि यह
(याद रखें कि यह  होना चाहिए)
होना चाहिए)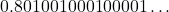
9. बताइए कि निम्नलिखित संख्याओं में कौन-कौन संख्याएँ परिमेय और कौन-कौन संख्याएँ अपरिमेय हैं।
किसी संख्या के परिमेय होने के लिए उसका दशमलव प्रसार ![]() या
या ![]() होना चाहिए, अन्यथा वह
होना चाहिए, अन्यथा वह ![]() होती है।
होती है।
| संख्या | दशमलव प्रसार / प्रकृति | प्रकार |
| (i) | अपरिमेय | |
| (ii) | परिमेय | |
| (iii) | यह एक | परिमेय |
| (iv) | यह | परिमेय |
| (v) | यह | अपरिमेय |