MP Board 9th Operations on real numbers वास्तविक संख्याओं पर संक्रियाएँ

MP Board 9th Operations on real numbers

MP Board 9th Operations on real numbers : पिछली कक्षाओं में, आप यह पढ़ चुके हैं कि परिमेय संख्याएँ योग और गुणन के क्रमविनिमय (commutative), साहचर्य (associative) और बंटन (distributive) नियमों को संतुष्ट करती हैं और हम यह भी पढ़ चुके हैं कि यदि हम दो परिमेय संख्याओं को जोड़ें, घटाएँ, गुणा करें या (शून्य छोड़कर) भाग दें, तब भी हमें एक परिमेय संख्या प्राप्त होती है [अर्थात् जोड़, घटाना, गुणा और भाग के सापेक्ष परिमेय संख्याएँ संवृत (closed) होती हैं]। यहाँ

हम यह भी देखते हैं कि अपरिमेय संख्याएँ भी योग और गुणन के क्रमविनिमय, साहचर्य और बंटन-नियमों को संतुष्ट करती हैं। परन्तु, अपरिमेय संख्याओं के योग, अंतर, भागफल और गुणनफल सदा अपरिमेय नहीं होते हैं। उदाहरण के लिए, $(\sqrt{2})-(\sqrt{2})$ , $(\sqrt{3})\cdot(\sqrt{3})$ और $\frac{\sqrt{17}}{\sqrt{17}}$ परिमेय संख्याएँ हैं।

WhatsApp Channel Join Now

Telegram Channel Join Now

आइए अब यह देखें कि जब एक परिमेय संख्या में अपरिमेय संख्या जोड़ते हैं और एक परिमेय संख्या को एक अपरिमेय संख्या से गुणा करते हैं, तो क्या होता है।

उदाहरण के लिए, $\sqrt{3}$ एक अपरिमेय संख्या है। तब $2+\sqrt{3}$ और $2\sqrt{3}$ क्या हैं? क्योंकि $\sqrt{3}$ एक अनवसानी अनावर्ती दशमलव प्रसार है, इसलिए यही बात $2+\sqrt{3}$ और $2\sqrt{3}$ के लिए भी सत्य है। अतः: $2+\sqrt{3}$ और $2\sqrt{3}$ भी अपरिमेय संख्याएँ हैं।

Here is the text from the image, transcribed exactly as it appears:

उदाहरण 11 जाँच कीजिए कि $\mathbf{7\sqrt{5}}$ , $\frac{\mathbf{7}}{\mathbf{\sqrt{5}}}$ , $\mathbf{\sqrt{2}+21}$ , $\mathbf{\pi-2}$ अपरिमेय संख्याएँ हैं या नहीं।

हल : $\sqrt{5} = 2.236...$ , $\sqrt{2} = 1.4142...$ , $\pi = 3.1415...$ है।

तब $7\sqrt{5} = 15.652...$ , $\frac{7}{\sqrt{5}} = \frac{7\sqrt{5}}{\sqrt{5}\sqrt{5}} = \frac{7\sqrt{5}}{5} = 3.1304...$ है।

$\sqrt{2}+21 = 22.4142...$ , $\pi-2 = 1.1415...$

ये सभी अनवसानी अनावर्ती दशमलव हैं। अतः: ये सभी अपरिमेय संख्याएँ हैं।

उदाहरण 12 $\mathbf{2\sqrt{2}+5\sqrt{3}}$ और $\mathbf{\sqrt{2}-3\sqrt{3}}$ को जोड़िए।

हल : $(2\sqrt{2}+5\sqrt{3})+(\sqrt{2}-3\sqrt{3}) = (2\sqrt{2}+\sqrt{2})+(5\sqrt{3}-3\sqrt{3})$

$= (2+1)\sqrt{2}+(5-3)\sqrt{3} = 3\sqrt{2}+2\sqrt{3}$

उदाहरण 13 : $\mathbf{6\sqrt{5}}$ को $\mathbf{2\sqrt{5}}$ से गुणा कीजिए।

हल : $6\sqrt{5} \times 2\sqrt{5} = 6 \times 2 \times \sqrt{5} \times \sqrt{5} = 12 \times 5 = 60$

उदाहरण 14 : $8\sqrt{15}$ को $2\sqrt{3}$ से भाग दीजिए।

हल : $8\sqrt{15} \div 2\sqrt{3} = \frac{8\sqrt{15}}{2\sqrt{3}} = \frac{8\sqrt{3 \times 5}}{2\sqrt{3}} = \frac{8\sqrt{3} \times \sqrt{5}}{2\sqrt{3}} = 4\sqrt{5}$

उदाहरण 16 : $\frac{1}{\sqrt{2}}$ के हर का परिमेयकरण कीजिए।

हल : $\frac{1}{\sqrt{2}} = \frac{1}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}} = \frac{\sqrt{2}}{2}$

चूँकि $\sqrt{2} \times \sqrt{2} = 2$

बिलकुल! अब मैं सभी गणितीय अभिव्यक्तियों को MathJax LaTeX फ़ॉर्मेट में के बीच लिखूंगा। आइए प्रश्नों को उसी तरह दोहराते हुए उत्तर देते हैं:

🌟 प्रश्न 1:

बताइए नीचे दी गई संख्याओं में कौन-कौन परिमेय है और कौन-कौन अपरिमेय है:

(i) $2 - \sqrt{5}$
(ii) $(3 + \sqrt{23}) - \sqrt{23}$
(iii) $\dfrac{2\sqrt{7}}{7\sqrt{7}}$
(iv) $\dfrac{1}{\sqrt{2}}$
(v) $2\pi$

उत्तर:

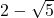(i) $2 - \sqrt{5}$ → $\sqrt{5}$ एक अपरिमेय संख्या है ⇒ यह अपरिमेय है।
(ii) $(3 + \sqrt{23}) - \sqrt{23} = 3$ ⇒ परिमेय है।
(iii) $\dfrac{2\sqrt{7}}{7\sqrt{7}} = \dfrac{2}{7}$ ⇒ परिमेय है।
(iv) $\dfrac{1}{\sqrt{2}}$ ⇒ अपरिमेय संख्या।
(v) 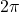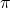$2\pi$ ⇒ $\pi$ अपरिमेय है ⇒ यह भी अपरिमेय है।

निष्कर्ष:
✅ परिमेय संख्याएँ: (ii), (iii)
❌ अपरिमेय संख्याएँ: (i), (iv), (v)

गणित के हल

कुछ सर्वसमिकाएँ (Identities)

मान लीजिए $a$ और $b$ धनात्मक वास्तविक संख्याएँ हैं। तब,

(i) $\sqrt{ab} = \sqrt{a}\sqrt{b}$
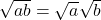
(ii) $\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}$
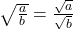
(iii) $(\sqrt{a}+\sqrt{b})(\sqrt{a}-\sqrt{b}) = a-b$
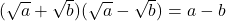
(iv) $(a+\sqrt{b})(a-\sqrt{b}) = a^2-b$
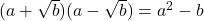
(v) $(\sqrt{a}+\sqrt{b})(\sqrt{c}+\sqrt{d}) = \sqrt{ac}+\sqrt{ad}+\sqrt{bc}+\sqrt{bd}$
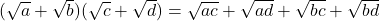
(vi) $(\sqrt{a}+\sqrt{b})^2 = a+2\sqrt{ab}+b$

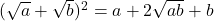
उदाहरण और हल

उदाहरण 14

प्रश्न: $8\sqrt{15}$ को $2\sqrt{3}$ से भाग दीजिए।

हल: $8\sqrt{15} \div 2\sqrt{3} = \frac{8\sqrt{15}}{2\sqrt{3}} = \frac{8\sqrt{3 \times 5}}{2\sqrt{3}} = \frac{8\sqrt{3} \times \sqrt{5}}{2\sqrt{3}} = 4\sqrt{5}$

उदाहरण 15

प्रश्न: निम्नलिखित व्यंजकों को सरल कीजिए:

(i) $(5+\sqrt{7})(2+\sqrt{5})$

हल: $10+5\sqrt{5}+2\sqrt{7}+\sqrt{35}$

(ii) $(5+\sqrt{5})(5-\sqrt{5})$

हल: $5^2 - (\sqrt{5})^2 = 25 - 5 = 20$

(iii) $(\sqrt{3}+\sqrt{7})^2$

हल: $(\sqrt{3})^2+2\sqrt{3}\sqrt{7}+(\sqrt{7})^2 = 3+2\sqrt{21}+7 = 10+2\sqrt{21}$

(iv) $(\sqrt{11}-\sqrt{7})(\sqrt{11}+\sqrt{7})$

हल: $(\sqrt{11})^2 - (\sqrt{7})^2 = 11 - 7 = 4$

उदाहरण 16

प्रश्न: $\frac{1}{\sqrt{2}}$ के हर का परिमेयकरण कीजिए।

हल: $\frac{1}{\sqrt{2}} = \frac{1}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}} = \frac{\sqrt{2}}{2}$

उदाहरण 17

प्रश्न: $\frac{1}{2+\sqrt{3}}$ के हर का परिमेयकरण कीजिए।

हल: $\frac{1}{2+\sqrt{3}} \times \frac{2-\sqrt{3}}{2-\sqrt{3}} = \frac{2-\sqrt{3}}{2^2 - (\sqrt{3})^2} = \frac{2-\sqrt{3}}{4-3} = 2-\sqrt{3}$

उदाहरण 18

प्रश्न: $\frac{5}{\sqrt{3}-\sqrt{5}}$ के हर का परिमेयकरण कीजिए।

हल: $\frac{5}{\sqrt{3}-\sqrt{5}} \times \frac{\sqrt{3}+\sqrt{5}}{\sqrt{3}+\sqrt{5}} = \frac{5(\sqrt{3}+\sqrt{5})}{(\sqrt{3})^2 - (\sqrt{5})^2} = \frac{5(\sqrt{3}+\sqrt{5})}{3-5} = -\frac{5}{2}(\sqrt{3}+\sqrt{5})$

उदाहरण 19

प्रश्न: $\frac{1}{7+3\sqrt{2}}$ के हर का परिमेयकरण कीजिए।

हल: $\frac{1}{7+3\sqrt{2}} \times \frac{7-3\sqrt{2}}{7-3\sqrt{2}} = \frac{7-3\sqrt{2}}{7^2 - (3\sqrt{2})^2} = \frac{7-3\sqrt{2}}{49-18} = \frac{7-3\sqrt{2}}{31}$

प्रश्नावली 1.5 से प्रश्न

प्रश्न 2

प्रश्न: निम्नलिखित व्यंजकों में से प्रत्येक व्यंजक को सरल कीजिए:

(i) $(3+\sqrt{3})(2+\sqrt{2})$

हल: $3 \times 2 + 3\sqrt{2} + 2\sqrt{3} + \sqrt{3}\sqrt{2} = 6+3\sqrt{2}+2\sqrt{3}+\sqrt{6}$

(ii) $(3+\sqrt{3})(3-\sqrt{3})$

हल: $3^2 - (\sqrt{3})^2 = 9 - 3 = 6$

(iii) $(\sqrt{5}+\sqrt{2})^2$

हल: $(\sqrt{5})^2 + 2\sqrt{5}\sqrt{2} + (\sqrt{2})^2 = 5 + 2\sqrt{10} + 2 = 7+2\sqrt{10}$

(iv) $(\sqrt{5}-\sqrt{2})(\sqrt{5}+\sqrt{2})$

हल: $(\sqrt{5})^2 - (\sqrt{2})^2 = 5 - 2 = 3$

प्रश्न 5

प्रश्न: निम्नलिखित के हरों का परिमेयकरण कीजिए:

(i) $\frac{1}{\sqrt{7}}$

हल: $\frac{1}{\sqrt{7}} \times \frac{\sqrt{7}}{\sqrt{7}} = \frac{\sqrt{7}}{7}$

(ii) $\frac{1}{\sqrt{7}-\sqrt{6}}$

हल: $\frac{1}{\sqrt{7}-\sqrt{6}} \times \frac{\sqrt{7}+\sqrt{6}}{\sqrt{7}+\sqrt{6}} = \frac{\sqrt{7}+\sqrt{6}}{7-6} = \sqrt{7}+\sqrt{6}$

(iii) $\frac{1}{\sqrt{5}+\sqrt{2}}$

हल: $\frac{1}{\sqrt{5}+\sqrt{2}} \times \frac{\sqrt{5}-\sqrt{2}}{\sqrt{5}-\sqrt{2}} = \frac{\sqrt{5}-\sqrt{2}}{5-2} = \frac{\sqrt{5}-\sqrt{2}}{3}$

(iv) $\frac{1}{\sqrt{7}-2}$

हल: $\frac{1}{\sqrt{7}-2} \times \frac{\sqrt{7}+2}{\sqrt{7}+2} = \frac{\sqrt{7}+2}{7-4} = \frac{\sqrt{7}+2}{3}$