गाउस नियम: वैद्युत फ्लक्स का एक सरल परिचय
MP Board 12th Physics Gauss’s Law : वैद्युत फ्लक्स की अवधारणा को और गहराई से समझने के लिए, आइए एक ऐसे काल्पनिक गोले से गुजरने वाले कुल फ्लक्स के बारे में सोचें जिसकी त्रिज्या r है और जिसके केंद्र में एक बिंदु आवेश q स्थित है।
हम इस गोले को बहुत छोटे क्षेत्रफल अवयवों में विभाजित करते हैं। किसी एक छोटे क्षेत्रफल अवयव ΔS से गुजरने वाला फ्लक्स इस प्रकार दिया जाता है:
![\[\Delta\phi = \vec{E} \cdot \Delta\vec{S} = \frac{1}{4\pi\epsilon_0} \frac{q}{r^2}\hat{r} \cdot \Delta\vec{S}\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-3dd2658fdb7cfcbbe95fe7ff21b0fa95_l3.png "Rendered by QuickLaTeX.com")
यह समीकरण कूलॉम नियम से लिया गया है जो एकल आवेश q के कारण उत्पन्न विद्युत क्षेत्र को दर्शाता है। यहाँ, एकांक सदिश r^ केंद्र से क्षेत्रफल अवयव तक की रेडियल दिशा में है।
चूंकि गोले की सतह पर किसी भी बिंदु पर, अभिलंब (normal) उस बिंदु पर ध्रुवांतर रेखा (radial line) के अनुदिश होता है, इसलिए क्षेत्रफल अवयव ΔS और एकांक सदिश r^ दोनों एक ही दिशा में होते हैं। इसलिए, हम समीकरण को इस प्रकार लिख सकते हैं:
![\[\Delta\phi = \frac{1}{4\pi\epsilon_0} \frac{q}{r^2}\Delta S\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-bcbf2c050121b89e257eea1763fd67d4_l3.png "Rendered by QuickLaTeX.com")
अब, गोले से गुजरने वाला कुल फ्लक्स प्राप्त करने के लिए हम सभी क्षेत्रफल अवयवों से गुजरने वाले फ्लक्सों को जोड़ते हैं:
![\[\phi = \sum_{\text{सभी }\Delta S} \frac{1}{4\pi\epsilon_0} \frac{q}{r^2}\Delta S\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-a1209f7dd9b43834759e26d3c7f8f695_l3.png "Rendered by QuickLaTeX.com")
चूंकि गोले का प्रत्येक क्षेत्रफल अवयव आवेश q से समान दूरी r पर है, हम समीकरण को सरल कर सकते हैं:
![\[\phi = \frac{q}{4\pi\epsilon_0r^2}(4\pi r^2) = \frac{q}{\epsilon_0}\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-69259f476ae9effc850c56a58482be2f_l3.png "Rendered by QuickLaTeX.com")
सभी छोटे क्षेत्रफल अवयवों का योग गोले का कुल पृष्ठीय क्षेत्रफल S देता है। चूँकि गोले का कुल पृष्ठीय क्षेत्रफल S=4πr2 होता है, इसलिए:
![\[\phi = \frac{q}{\epsilon_0}\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-6d3d208ef106806371732cd1c45a8da2_l3.png "Rendered by QuickLaTeX.com")
यह परिणाम, गाउस नियम के एक सरल उदाहरण को दर्शाता है। गाउस नियम का सबसे सरल रूप इस प्रकार है:
किसी भी बंद पृष्ठ S से गुजरने वाला वैद्युत फ्लक्स उस पृष्ठ द्वारा परिबद्ध कुल आवेश q का ϵ01 गुना होता है।ϕ=ϵ0q
इस नियम का एक महत्वपूर्ण निष्कर्ष यह है कि यदि किसी बंद पृष्ठ में कोई आवेश नहीं है, तो उस पृष्ठ से गुजरने वाला कुल फ्लक्स शून्य होता है। हम इसे एक सरल स्थिति से समझ सकते हैं।
एकसमान विद्युत क्षेत्र में बेलन
आइए एकसमान विद्युत क्षेत्र E में एक बंद बेलनाकार पृष्ठ पर विचार करें जिसका अक्ष E के समानांतर है। इस पृष्ठ से गुजरने वाला कुल फ्लक्स ϕ=ϕ1+ϕ2+ϕ3 है।
- ϕ1 और ϕ2 बेलन के वृत्ताकार अनुप्रस्थ परिच्छेद से गुजरने वाले फ्लक्स हैं।
- ϕ3 बेलन के घुमावदार (curved) भाग से गुजरने वाला फ्लक्स है।
चूंकि घुमावदार भाग के प्रत्येक बिंदु पर अभिलंब E के लंबवत होता है, इसलिए ϕ3=0।
इसके अलावा, पृष्ठ 2 पर बाहर की ओर का अभिलंब E की दिशा में है, और पृष्ठ 1 पर बाहर की ओर का अभिलंब E की दिशा के विपरीत है। इसलिए:ϕ1=−ES1ϕ2=+ES2
जहां S1=S2=S है, जो वृत्ताकार अनुप्रस्थ काट का क्षेत्रफल है। इस प्रकार, कुल फ्लक्स ϕ=−ES+ES=0 है, जैसा कि गाउस नियम से अपेक्षित था।
गाउस नियम के महत्वपूर्ण तथ्य
गाउस नियम के कुछ महत्वपूर्ण पहलू हैं जिन्हें आपको हमेशा ध्यान में रखना चाहिए:
- सत्यता: गाउस नियम किसी भी बंद पृष्ठ के लिए सत्य है, चाहे उसकी आकृति और आकार कुछ भी हो।
- आवेश की स्थिति: समीकरण के दाईं ओर का पद q पृष्ठ के भीतर स्थित सभी आवेशों का योग है।
- विद्युत क्षेत्र: फ्लक्स समीकरण में विद्युत क्षेत्र (E) का पद पृष्ठ के अंदर और बाहर स्थित सभी आवेशों के कारण होता है। हालांकि, समीकरण के दाईं ओर का पद q केवल अंदर के आवेशों को दर्शाता है।
- गाउसीय पृष्ठ: गाउस नियम के लिए चुने गए पृष्ठ को गाउसीय पृष्ठ कहा जाता है। इसे किसी भी अलग-अलग (discrete) आवेश से होकर नहीं गुजरना चाहिए क्योंकि इन बिंदुओं पर विद्युत क्षेत्र को परिभाषित नहीं किया जा सकता है।
- सममिति: जब किसी निकाय में सममिति होती है, तो गाउस नियम विद्युत क्षेत्र की गणना को बहुत आसान बना सकता है।
अक्सर पूछे जाने वाले प्रश्न (FAQs)
- गाउस नियम क्या है?
- गाउस नियम बताता है कि किसी बंद पृष्ठ से गुजरने वाला कुल वैद्युत फ्लक्स उस पृष्ठ के अंदर मौजूद कुल आवेश का ϵ01 गुना होता है।
- गाउसीय पृष्ठ क्या होता है?
- गाउसीय पृष्ठ एक काल्पनिक बंद पृष्ठ होता है जिसका उपयोग गाउस नियम को लागू करने के लिए किया जाता है। इसे इस तरह से चुना जाता है कि यह किसी भी अलग-अलग आवेश से होकर न गुजरे।
- अगर किसी बंद पृष्ठ के अंदर कोई आवेश न हो तो क्या होता है?
- गाउस नियम के अनुसार, यदि किसी बंद पृष्ठ के अंदर कोई कुल आवेश नहीं है, तो उस पृष्ठ से गुजरने वाला कुल वैद्युत फ्लक्स शून्य होता है।
- गाउस नियम इतना महत्वपूर्ण क्यों है?
- गाउस नियम एक बहुत ही व्यापक नियम है जो किसी भी बंद पृष्ठ के लिए सत्य है, चाहे उसका आकार या आकृति कुछ भी हो। यह विशेष रूप से तब उपयोगी होता है जब निकाय में कुछ सममिति होती है, जिससे विद्युत क्षेत्र की गणना करना आसान हो जाता है।
- गाउस नियम और कूलॉम नियम के बीच क्या संबंध है?
- गाउस नियम कूलॉम नियम में निहित दूरी पर व्युत्क्रम वर्ग निर्भरता पर आधारित है। इसका मतलब है कि गाउस नियम का कोई भी उल्लंघन व्युत्क्रम वर्ग नियम से विचलन का संकेत देगा।
उदाहरण 1.10 का हल :
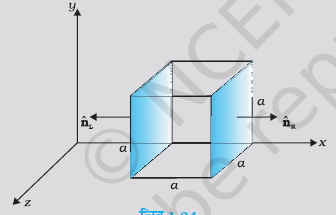
चित्र 1.24 में विद्युत क्षेत्र अवयव Ex=αx1/2, Ey=Ez=0 है, जिसमें α=800 N/C m1/2 है। (a) घन से गुजरने वाला फ्लक्स, तथा (b) घन के भीतर आवेश परिकलित कीजिए। a=0.1 m मानिए।
प्रश्न के अनुसार, एक घन है जिसकी भुजा की लंबाई a है। विद्युत क्षेत्र केवल x-अक्ष के अनुदिश है और Ex=αx1/2 है, जहाँ α=800N/C m1/2 और a=0.1m है।
(a) घन से गुजरने वाला कुल फ्लक्स (ϕ)
कुल फ्लक्स की गणना के लिए, हम घन के प्रत्येक फलक से गुजरने वाले फ्लक्स की गणना करते हैं। चूँकि विद्युत क्षेत्र केवल x-अक्ष के अनुदिश है, इसलिए केवल y−z तल के समानांतर फलक ही फ्लक्स में योगदान देंगे। अन्य सभी फलकों के लिए, क्षेत्रफल सदिश S विद्युत क्षेत्र E
के लंबवत होगा, इसलिए उनसे गुजरने वाला फ्लक्स शून्य होगा।
बाएं फलक (Left Face): बाएं फलक पर, x=0 है।
![\[\phi_L = \vec{E} \cdot \vec{S} = (\alpha x^{1/2}) \cdot S \cdot \cos(180^\circ)\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-fb46bedd1adfaeee24b7f4bc53c8c183_l3.png "Rendered by QuickLaTeX.com")
, 
होगा। इसलिए, ![\[\phi_L = 0\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-edee5c7beee44008620d77da43d76476_l3.png "Rendered by QuickLaTeX.com")
दाएं फलक (Right Face): दाएं फलक पर, x=a=0.1m है।
![\[\phi_R = \vec{E} \cdot \vec{S} = (\alpha x^{1/2}) \cdot S \cdot \cos(0^\circ)\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-4c3ef782693202b11ed91ce0f09db132_l3.png "Rendered by QuickLaTeX.com")
![\[E_x = 800 \times (0.1)^{1/2} = 800 \times 0.3162 = 252.98 \, \text{N/C}\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-6ecb24d7d3112a06475b275104b32515_l3.png "Rendered by QuickLaTeX.com")
![\[\phi_R = 252.98 \times 0.01 = 2.53 \, \text{N m}^2/\text{C}\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-28dbea906ba41f2bec40a62d134a1844_l3.png "Rendered by QuickLaTeX.com")
कुल फ्लक्स: अन्य चार फलकों से गुजरने वाला फ्लक्स शून्य है।
ϕtotal=ϕL+ϕR=0+2.53=2.53N m2/C
(b) घन के भीतर कुल आवेश (q)
गाउस नियम के अनुसार,
![\[\phi_{total} = \frac{q}{\epsilon_0}\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-4f89989f752a8f365152c30f795639ce_l3.png "Rendered by QuickLaTeX.com")
q=ϕtotal×ϵ0
जहाँ ϵ0=8.854×10−12C2/N m2 है।
q=2.53×(8.854×10−12)=2.24×10−11C
उदाहरण 1.11 का हल : कोई विद्युत क्षेत्र धनात्मक x के लिए, धनात्मक x दिशा में एकसमान है तथा उसी परिमाण के साथ परंतु ऋणात्मक x के लिए, ऋणात्मक x दिशा में एकसमान है। यह दिया गया है कि E=200i^ N/C जबकि x>0 तथा E=−200i^ N/C, जबकि x<0 है। 20 cm लंबे 5 cm त्रिज्या के किसी लंबवृत्तीय सिलिंडर का केंद्र मूल बिंदु पर तथा इस अक्ष x के इस प्रकार अनुदिश है कि इसका एक फलक चित्र 1.25 में दर्शाए अनुसार x=+10 cm तथा दूसरा फलक x=−10 cm पर है। (a) प्रत्येक चपटे फलक से गुजरने वाला नेट बहिर्मुखी फ्लक्स कितना है? (b) सिलिंडर के पार्श्व से गुजरने वाला फ्लक्स कितना है? (c) सिलिंडर से गुजरने वाला नेट बहिर्मुखी फ्लक्स कितना है? (d) सिलिंडर के भीतर नेट आवेश कितना है?
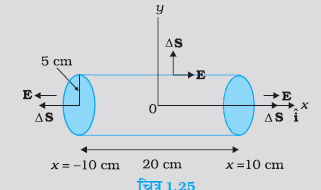
प्रश्न के अनुसार, एक लंबवृत्तीय बेलन है जिसकी लंबाई 20cm और त्रिज्या 5cm है। इसका केंद्र मूल बिंदु पर है और इसका अक्ष x-अक्ष के अनुदिश है।
- x>0 के लिए, E
=200i^N/C
- x<0 के लिए, E
=−200i^N/C
(a) प्रत्येक चपटे फलक से गुजरने वाला फ्लक्स
बेलन के दो चपटे फलक हैं। दायाँ फलक (Right Face): यह फलक x=+10cm=+0.1m पर है। यहाँ, विद्युत क्षेत्र E धनात्मक x-दिशा में है। बाहर की ओर का क्षेत्रफल सदिश S
भी उसी दिशा में है।
![\[\phi_R = \vec{E} \cdot \vec{S} = ES \cos(0^\circ) = (200) \times (\pi r^2)\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-513db1db98c264c795e22ae032e23ce1_l3.png "Rendered by QuickLaTeX.com")
है। ![\[\phi_R = 200 \times \pi (0.05)^2 = 200 \times 3.1416 \times 0.0025 = 1.57 \, \text{N m}^2/\text{C}\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-1b82ce58bf04075a68408ee44d309406_l3.png "Rendered by QuickLaTeX.com")
बायां फलक (Left Face): यह फलक x=−10cm=−0.1m पर है। यहाँ, विद्युत क्षेत्र E ऋणात्मक x-दिशा में है। बाहर की ओर का क्षेत्रफल सदिश S
भी ऋणात्मक x-दिशा में है।
ϕL=E⋅S
=EScos(0∘)=(200)×(πr2)
ϕL=200×π(0.05)2=1.57N m2/C
प्रत्येक चपटे फलक से गुजरने वाला फ्लक्स 1.57N m2/C है।
(b) बेलन के पार्श्व (curved) से गुजरने वाला फ्लक्स
बेलन के पार्श्व पर, क्षेत्रफल सदिश S हमेशा विद्युत क्षेत्र E
के लंबवत होता है, क्योंकि E
केवल x-अक्ष के अनुदिश है। इसलिए,
ϕside=E⋅S
=EScos(90∘)=0
(c) बेलन से गुजरने वाला कुल फ्लक्स
कुल फ्लक्स सभी फलकों से गुजरने वाले फ्लक्सों का योग है:
ϕtotal=ϕR+ϕL+ϕside=1.57+1.57+0=3.14N m2/C
(d) बेलन के भीतर कुल आवेश
गाउस नियम के अनुसार,
q=ϕtotal×ϵ0
जहाँ ϵ0=8.854×10−12C2/N m2 है।
q=3.14×(8.854×10−12)=2.78×10−11C