वैद्युत द्विध्रुव MP Board 12th Physics Electric Dipole
MP Board 12th Physics Electric Dipole : एक वैद्युत द्विध्रुव समान और विपरीत बिंदु आवेशों, +q और −q का एक युग्म होता है, जो 2a की दूरी से अलग होते हैं। दोनों आवेशों को जोड़ने वाली रेखा अंतरिक्ष में एक दिशा को परिभाषित करती है। परिपाटी के अनुसार, द्विध्रुव की दिशा ऋणात्मक आवेश से धनात्मक आवेश की ओर होती है। आवेशों −q और +q की स्थितियों का मध्य बिंदु द्विध्रुव का केंद्र कहलाता है।
एक वैद्युत द्विध्रुव का कुल आवेश शून्य होता है। तथापि, इसका यह अर्थ नहीं है कि वैद्युत द्विध्रुव का वैद्युत क्षेत्र शून्य है। चूँकि आवेश −q और +q कुछ दूरी से पृथक होते हैं, इनके कारण वैद्युत क्षेत्र जब जोड़े जाते हैं तब वे एक-दूसरे को यथार्थ रूप से निरस्त नहीं करते। परंतु यदि द्विध्रुव बनाने वाले आवेशों के पृथकन की तुलना में दूरी अधिक (r>>2a) हो, तो q एवं −q के कारण क्षेत्र लगभग निरस्त हो जाते हैं। अतः, अधिक दूरियों पर किसी वैद्युत द्विध्रुव के कारण वैद्युत क्षेत्र 1/r3 के रूप में मंद होता जाता है, जबकि एक एकल आवेश के कारण वैद्युत क्षेत्र 1/r2 के रूप में मंद होता है।
1.10.1 वैद्युत द्विध्रुव के कारण क्षेत्र
आवेशों के युग्म (−q तथा +q) के कारण दिक्स्थान में किसी बिंदु पर वैद्युत क्षेत्र कूलॉम नियम तथा अध्यारोपण सिद्धांत से ज्ञात किया जा सकता है। निम्नलिखित दो प्रकारों के परिणाम सरल हैं: (i) जब बिंदु द्विध्रुव के अक्ष पर है, (ii) जब बिंदु द्विध्रुव के विषुवतीय तल, अर्थात् द्विध्रुव अक्ष के केंद्र से गुजरने वाले द्विध्रुव अक्ष के लंबवत तल में है। किसी व्यापक बिंदु P पर वैद्युत क्षेत्र, आवेश −q के कारण P पर वैद्युत क्षेत्र E−q तथा आवेश +q के कारण P पर वैद्युत क्षेत्र E+q को सदिशों के समांतर चतुर्भुज नियम द्वारा संयोजित करके प्राप्त किया जाता है।
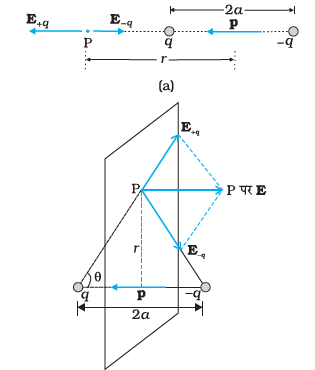
(i) अक्ष पर स्थित बिंदुओं के लिए
मान लीजिए बिंदु P द्विध्रुव के केंद्र से q की ओर r दूरी पर है। तब −q के कारण वैद्युत क्षेत्र है:
![]()
यहाँ p^ द्विध्रुव अक्ष (−q से q की ओर) के अनुदिश एकांक सदिश है। और +q के कारण वैद्युत क्षेत्र है:
![]()
P पर कुल वैद्युत क्षेत्र है:
![]()
![]()
r>>a के लिए, व्यंजक सरल हो जाता है:
![]()
(ii) विषुवतीय तल पर स्थित बिंदुओं के लिए
दो आवेशों, +q और −q के कारण वैद्युत क्षेत्रों के परिमाण समान हैं:
![]()
![]()
E+q तथा E−q की दिशाएँ चित्र 1.17(b) में दर्शाई गई हैं। यह स्पष्ट है कि द्विध्रुव अक्ष के अभिलंबवत अवयव एक-दूसरे को निरस्त कर देते हैं। द्विध्रुव अक्ष के अनुदिश अवयव संयोजित हो जाते हैं। कुल वैद्युत क्षेत्र E की दिशा p^ के विपरीत होती है। अतः:
![]()
![]()
अधिक दूरियों (r>>a) के लिए, व्यंजक सरल हो जाता है:
![]()
द्विध्रुव आघूर्ण
समीकरणों (1.15) तथा (1.18) से यह स्पष्ट है कि अधिक दूरियों पर द्विध्रुव क्षेत्र q तथा a पर पृथक रूप से सम्मिलित नहीं होते; इससे द्विध्रुव आघूर्ण की परिभाषा का संकेत मिलता है। किसी वैद्युत द्विध्रुव के द्विध्रुव आघूर्ण सदिश p की परिभाषा इस प्रकार की जा सकती है:
![]()
अतः, द्विध्रुव आघूर्ण एक सदिश है जिसका परिमाण q×2a तथा इसकी दिशा −q से +q की ओर होती है। p के पदों में, किसी द्विध्रुव का वैद्युत क्षेत्र अधिक दूरियों पर एक सरल रूप ले लेता है।
द्विध्रुव अक्ष के किसी बिंदु पर:
![]()
विषुवतीय तल के किसी बिंदु पर:
![]()
बिंदु द्विध्रुव
यह महत्वपूर्ण तथ्य पर ध्यान दीजिए कि द्विध्रुव क्षेत्र अधिक दूरियों पर 1/r3 के रूप में मंद होता है। इसके अतिरिक्त द्विध्रुव क्षेत्र का परिमाण तथा दिशा केवल दूरी r पर निर्भर नहीं है वरन् यह सदिश r तथा द्विध्रुव आघूर्ण p के बीच के कोण पर भी निर्भर करते हैं।
हम उसके बारे में सोच सकते हैं- जब द्विध्रुव आमाप 2a शून्य की ओर अग्रसर होता जाता है, तब आवेश q अनंत की ओर अग्रसर इस प्रकार होता जाता है कि गुणनफल p=q×2a एक नियत परिमित संख्या होती है। इस प्रकार के द्विध्रुव को बिंदु द्विध्रुव कहते हैं। किसी बिंदु द्विध्रुव के लिए समीकरण (1.20) तथा (1.21) r के सभी मानों के लिए सत्य यथार्थ हैं।
उदाहरण 1.9 का हल
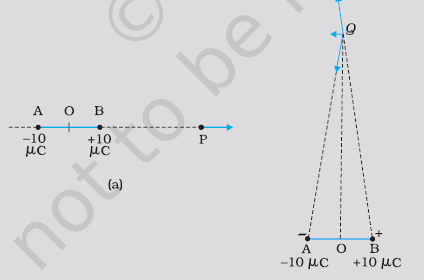
प्रश्न: ±10μC के दो आवेश एक-दूसरे से 5.0mm की दूरी पर स्थित हैं। (a) इस द्विध्रुव के अक्ष पर, द्विध्रुव के केंद्र O से 15cm दूरी पर स्थित किसी बिंदु P पर तथा (b) द्विध्रुव के अक्ष के अभिलंबवत, O से गुजरने वाली रेखा पर 15cm दूरी पर स्थित किसी बिंदु Q पर वैद्युत क्षेत्र ज्ञात कीजिए।
±10 μC±10μC के दो आवेश 5.0 mm दूरी पर स्थित हैं।
(a) धन आवेश की ओर 15 cm दूरी पर स्थित बिंदु P पर तथा
(b) ऋण आवेश की ओर 15 cm दूरी पर स्थित बिंदु Q पर
विद्युत क्षेत्र ज्ञात कीजिए।
दिए गए मान
- धन आवेश (Q1Q1) =+10 μC=+10×10−6 C=+10μC=+10×10−6C
- ऋण आवेश (Q2Q2) =−10 μC=−10×10−6 C=−10μC=−10×10−6C
- दोनों के बीच दूरी (dd) =5.0 mm=5.0×10−3 m=5.0mm=5.0×10−3m
- बिंदु P और Q तक आवेशों से दूरी (rr) =15 cm=0.15 m=15cm=0.15m
विद्युत क्षेत्र का सूत्र
किसी बिंदु आवेश QQ से दूरी rr पर विद्युत क्षेत्र:
![]()
जहाँ
![]()
(a) धन आवेश की ओर बिंदु P पर विद्युत क्षेत्र
Step 1: बिंदु P तक धन एवं ऋण आवेशों की दूरी
धन आवेश से दूरी: r1=0.15 mr1=0.15m
ऋण आवेश से दूरी: r2=d+r1=0.005+0.15=0.155 mr2=d+r1=0.005+0.15=0.155m
Step 2: दोनों आवेशों द्वारा उत्पन्न विद्युत क्षेत्र
धन आवेश द्वारा:
![]()
ऋण आवेश द्वारा:
![]()
Step 3: परिणामिक विद्युत क्षेत्र (दोनों का योग)
![]()
(b) ऋण आवेश की ओर बिंदु Q पर विद्युत क्षेत्र
Step 1: बिंदु Q तक धन एवं ऋण आवेशों की दूरी
ऋण आवेश से दूरी: r1′=0.15 mr1′=0.15m
धन आवेश से दूरी: r2′=d+r1′=0.005+0.15=0.155 mr2′=d+r1′=0.005+0.15=0.155m
Step 2: दोनों आवेशों द्वारा उत्पन्न विद्युत क्षेत्र
ऋण आवेश द्वारा:
![]()
धन आवेश द्वारा:
![]()
Step 3: परिणामिक विद्युत क्षेत्र (दोनों का योग)
![]()
मानों की गणना (Numerical Calculation):
(a) बिंदु P:
![]()
![]()
![]()
(b) बिंदु Q:
![]()
![]()
![]()
अंतिम उत्तर
- बिंदु P (धन आवेश की ओर):
![Rendered by QuickLaTeX.com \[E_{net} = 2.54 \times 10^5, \text{N/C}\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-241fc1283bbed559ab39febb2158dec4_l3.png)
- बिंदु Q (ऋण आवेश की ओर):
![Rendered by QuickLaTeX.com \[E'_{net} = -2.54 \times 10^5, \text{N/C}\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-04706a8051b8f8543a98d52e255d5890_l3.png)
MP Board 12th Physics Electric Dipole अक्सर पूछे जाने वाले प्रश्न (FAQs)
1. वैद्युत द्विध्रुव (Electric Dipole) क्या है?
दो समान परिमाण और विपरीत प्रकृति (+q और −q) के बिंदु आवेश, जो एक दूसरे से बहुत कम दूरी (2a) पर स्थित होते हैं, एक वैद्युत द्विध्रुव का निर्माण करते हैं।
2. वैद्युत द्विध्रुव आघूर्ण क्या है?
वैद्युत द्विध्रुव आघूर्ण (p) एक सदिश राशि है जिसका परिमाण एक आवेश (q) और दो आवेशों के बीच की दूरी (2a) के गुणनफल के बराबर होता है, यानी p=q×2a। इसकी दिशा ऋणात्मक आवेश से धनात्मक आवेश की ओर होती है।
3. द्विध्रुव के कारण वैद्युत क्षेत्र दूरी (r) के साथ कैसे बदलता है?
किसी द्विध्रुव के कारण वैद्युत क्षेत्र अधिक दूरी (r>>a) पर दूरी के घन (1/r3) के व्युत्क्रमानुपाती होता है, जबकि एकल आवेश के लिए यह दूरी के वर्ग (1/r2) के व्युत्क्रमानुपाती होता है।