MP Board 12th Mathematics Relation And Function Question Bank : कक्षा 12 गणित अध्याय-1: संबंध एवं फलन प्रश्न बैंक
अध्याय-1: संबंध एवं फलन
जी, बिल्कुल। इमेज में दिए गए तथ्यों को उसी तरह एक-एक लाइन में यहाँ प्रस्तुत किया गया है:
स्मरणीय बिंदु :
इस अध्याय में हमने विविध प्रकार के संबंधों, फलनों तथा द्विआधारी संक्रियाओं का अध्ययन किया है।
इस अध्याय की मुख्य विषय-वस्तु निम्नलिखित है:
Xमें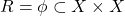 द्वारा प्रदत्त संबंध R रिक्त संबंध होता है।
द्वारा प्रदत्त संबंध R रिक्त संबंध होता है।Xमें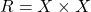 द्वारा प्रदत्त संबंध R सार्वत्रिक संबंध है।
द्वारा प्रदत्त संबंध R सार्वत्रिक संबंध है।Xमें R ऐसा संबंध कि , R स्वतुल्य संबंध है।
, R स्वतुल्य संबंध है।Xमें इस प्रकार का संबंध R, जो प्रतिबंध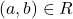 का तात्पर्य है कि
का तात्पर्य है कि 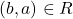 को संतुष्ट करता है, सममित संबंध है।
को संतुष्ट करता है, सममित संबंध है।Xमें R प्रतिबंध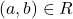 तथा
तथा 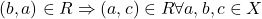 को संतुष्ट करने वाला संबंध R संक्रामक संबंध है।
को संतुष्ट करने वाला संबंध R संक्रामक संबंध है।Xमें संबंध R, जो स्वतुल्य, सममित तथा संक्रामक है, तुल्यता संबंध है।Xमें R किसी तुल्यता संबंध R के लिए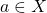 के संगत तुल्यता वर्ग
के संगत तुल्यता वर्ग![Rendered by QuickLaTeX.com [a]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-46276474876165ad906e954f72d71b61_l3.png) , X का वह उपसमुच्चय है जिसके सभी अवयव a से संबंधित हैं।
, X का वह उपसमुच्चय है जिसके सभी अवयव a से संबंधित हैं।- एक फलन
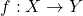 एकैकी (अथवा एकैक) फलन है
एकैकी (अथवा एकैक) फलन है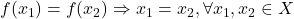 एक फलन
एक फलन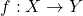 आच्छादक (अथवा आच्छादी) फलन है यदि किसी प्रदत्त
आच्छादक (अथवा आच्छादी) फलन है यदि किसी प्रदत्त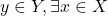 , इस प्रकार कि
, इस प्रकार कि 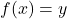 * एक फलन
* एक फलन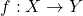 एकैकी तथा आच्छादक (अथवा एकैकी आच्छादक) फलन है यदि
एकैकी तथा आच्छादक (अथवा एकैकी आच्छादक) फलन है यदि एकैकी तथा अच्छादक दोनों है।
एकैकी तथा अच्छादक दोनों है। - किसी प्रदत्त परिमित समुच्चय
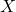 के लिए फलन
के लिए फलन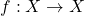 एकैकी तदानुसार आच्छादक होता है यदि और केवल यदि
एकैकी तदानुसार आच्छादक होता है यदि और केवल यदि आच्छादक तदानुसार एकैकी है। यह किसी परिमित समुच्चय का अभिलाक्षणिक गुणधर्म (Characteristic Property) है। यह अपरिमित समुच्चय के लिए सत्य नहीं है।
आच्छादक तदानुसार एकैकी है। यह किसी परिमित समुच्चय का अभिलाक्षणिक गुणधर्म (Characteristic Property) है। यह अपरिमित समुच्चय के लिए सत्य नहीं है।
प्रश्न 1. सही विकल्प चुनिए –
(i) यदि समुच्चय {1,2,3} में R=(1,1),(2,2),(3,3)(1,2)(2,3) द्वारा प्रदत्त संबंध है :
(a) केवल सममित (b) केवल स्वतुल्य (b) केवल संक्रामक (c) एक तुल्यता संबंध
(ii) यदि फलन f:R→R जो f(x)=3x द्वारा परिभाषित है तो:
(a) एकैकी आच्छादक है।
(b) एकैकी है किन्तु आच्छादक नहीं है।
(c) आच्छादक है किन्तु एकैकी नहीं
(d) एकैकी आच्छादक दोनो नहीं है।
(iii) यदि फलन f:N→N जो f(x)=2x द्वारा परिभाषित है तो :
(a) एकैकी आच्छादक है।
(b) एकैकी है किन्तु आच्छादक नहीं है।
(c) आच्छादक है किन्तु एकैकी नहीं
(d) एकैकी आच्छादक दोनो नहीं है।
(iv) यदि समुच्चय {1,2,3,4} में R={(1,2),(2,2),(1,1),(4,4),(1,3),(3,3),(2,1),(3,1)} द्वारा प्रदत्त संबंध है तो:
(a) स्वतुल्य तथा सममित है किन्तु संक्रमक नहीं है।
(b) स्वतुल्य तथा संक्रामक है किन्तु सममित नहीं है।
(c) सममित तथा संक्रमक है किंतु स्वतुल्य नहीं है।
(d) एक तुल्यता संबंध है।
(v) यदि समुच्चय ![]() में
में ![]() द्वारा प्रदत्त संबंध है तो:
द्वारा प्रदत्त संबंध है तो:
(a) स्वतुल्य तथा सममित है किन्तु संक्रमक नहीं है।
(b) स्वतुल्य तथा संक्रामक है किन्तु सममित नहीं है।
(c) सममित तथा संक्रमक है किंतु स्वतुल्य नहीं है।
(d) एक तुल्यता संबंध है।
(vi) यदि ![]() हो निम्न में से कौन सा तुल्यता संबंध नही है:
हो निम्न में से कौन सा तुल्यता संबंध नही है:
(a) ![]()
(b) ![]()
(c) ![]()
(d) इनमें से कोई नहीं
(vii) माना समुच्चय ![]() में
में ![]() द्वारा प्रदत्त संबंध है तब निम्न मे से सही उत्तर चुनिए:
द्वारा प्रदत्त संबंध है तब निम्न मे से सही उत्तर चुनिए:
(a) ![]()
(b) ![]()
(c) ![]()
(d) ![]()
(viii) यदि फलन ![]() किसी समुच्चय
किसी समुच्चय ![]() से
से ![]() पर परिभाषित है तब
पर परिभाषित है तब ![]() व्युत्क्रमणीय फलन होगा जब फलन अनिवार्यत हो:
व्युत्क्रमणीय फलन होगा जब फलन अनिवार्यत हो:
(a) एकैकी
(b) आच्छादक
(c) एकैकी एवं आच्छादक
(d) इनमें से कोई नहीं
(ix) माना ![]() रेखाओं के समुच्चय
रेखाओं के समुच्चय ![]() पर संबंध
पर संबंध ![]() = ‘रेखा
= ‘रेखा ![]() रेखा
रेखा ![]() पर लंबवत है’ द्वारा परिभाषित है तो
पर लंबवत है’ द्वारा परिभाषित है तो ![]() किस प्रकार का संबंध है:
किस प्रकार का संबंध है:
(a) स्वतुल्य एवं सममित
(b) सममित एवं संक्रामक
(c) तुल्यता संबंध
(d) सममित संबंध
(x) दिए गए समुच्चय A = {a,b,c} के लिए एक तत्समक संबंध होगा:
(a) ![]()
(b) ![]()
(c) ![]()
(d) ![]()
(xi) माना ![]() द्वारा परिभाषित है तो:
द्वारा परिभाषित है तो:
(a) ![]() एकैकी आच्छादक है।
एकैकी आच्छादक है।
(b) ![]() बहुएक आच्छादक नहीं है।
बहुएक आच्छादक नहीं है।
(c) ![]() एकैकी पर आच्छादक नहीं
एकैकी पर आच्छादक नहीं
(d) ![]() न एकैकी है और न आच्छादक।
न एकैकी है और न आच्छादक।
(xii) माना ![]() इस प्रकार परिभाषित है कि
इस प्रकार परिभाषित है कि ![]() जहाँ
जहाँ ![]() तब
तब ![]() होगा:
होगा:
(a) आच्छादक
(b) प्रतिलोम
(c) एकैकी
(d) इनमें से कोई नहीं
(xiii) यदि ![]() जहाँ
जहाँ ![]() तब
तब ![]() का मान होगा :
का मान होगा :
(a) 0
(b) 28
(c) 14
(d) 35
(xiv) माना समुच्चय ![]() और
और ![]() समुच्चय
समुच्चय ![]() पर परिभाषित संबंध इस प्रकार है कि
पर परिभाषित संबंध इस प्रकार है कि ![]() तब संबंध
तब संबंध ![]() होगा।
होगा।
(a) रिक्त संबंध
(b) स्वतुल्य संबंध
(c) सममित संबंध
(d) तुल्यता संबंध
(xv) माना ![]() एक सम्बंध
एक सम्बंध ![]() पर इस प्रकार परिभाषित है कि
पर इस प्रकार परिभाषित है कि ![]() तब
तब ![]() होगा
होगा
(a) सममित संक्रामक किन्तु स्वतुल्य नहीं।
(b) स्वतुल्य सममित किन्तु संक्रामक नहीं।
(c) स्वतुल्य और संक्रामक किन्तु सममित नहीं।
(d) एक तुल्यता संबंध
(xvi) माना ![]() और संबंध
और संबंध ![]() से
से ![]() पर इस प्रकार परिभाषित है कि
पर इस प्रकार परिभाषित है कि ![]() बड़ा है
बड़ा है ![]() से तब
से तब ![]() का परिसर क्या होगा
का परिसर क्या होगा
(a) ![]()
(b) ![]()
(c) ![]()
(d) इनमें से कोई नहीं
(xvii) यदि समुच्चय ![]() पर संबंध
पर संबंध ![]() इस प्रकार परिभाषित है कि
इस प्रकार परिभाषित है कि ![]() तब
तब ![]() बराबर है।
बराबर है।
(a) ![]()
(b) ![]()
(c) ![]()
(d) इनमें से कोई नहीं
(xviii) यदि ![]() हो तो अवयव (1,2) वाले तुल्यता संबंधों की संख्या है-
हो तो अवयव (1,2) वाले तुल्यता संबंधों की संख्या है-
(a) 1
(b) 2
(c) 3
(d) 4
(xix) ![]() में प्रतिबंध R,
में प्रतिबंध R, ![]() तथा
तथा ![]() जहाँ
जहाँ ![]() को संतुष्ट करने वाला सम्बंध R
को संतुष्ट करने वाला सम्बंध R
(a) सममित सम्बंध है।
(b) स्वतुल्य सम्बंध है।
(c) संक्रामक सम्बंध है।
(d) रिक्त सम्बंध है।
(xx) प्रदत्त सम्बंध ![]() रिक्त सम्बंध होगा यदि –
रिक्त सम्बंध होगा यदि –
(a) ![]()
(b) ![]()
(c) ![]()
(d) ![]()
(xxi) ![]() एक आच्छादक फलन होगा यदि –
एक आच्छादक फलन होगा यदि –
(a) ![]()
(b) ![]()
(c) ![]()
(d) ![]()
(xxii) मान लीजिये कि ![]() द्वारा परिभाषित फलन
द्वारा परिभाषित फलन ![]() है तब :
है तब :
(a) एकैकी आच्छादक
(b) बहुएक आच्छादक है।
(c) एकैकी है परन्तु आच्छादक नहीं
(d) न तो एकैकी है और न आच्छादक है।
(xxiii) यदि ![]() तथा
तथा ![]() तो
तो ![]()
(a) 6
(b) 2
(c) 4
(d) 3
(xxiv) ![]() में सम्बंध
में सम्बंध ![]() जो स्वतुल्य सममित तथा संक्रामक है वह सम्बंध कहलाता है –
जो स्वतुल्य सममित तथा संक्रामक है वह सम्बंध कहलाता है –
(a) तुल्यता सम्बंध
(b) सार्वत्रिक सम्बंध
(c) रिक्त सम्बंध
(d) सममित सम्बंध
प्रश्न 2. रिक्त स्थानो की पूर्ति कीजिए :
(i) समुच्चय ![]() पर परिभाषित कोई संबंध
पर परिभाषित कोई संबंध ![]() स्वतुल्य, सममित तथा संक्रामक है तो
स्वतुल्य, सममित तथा संक्रामक है तो ![]() एक —— कहलाता है।
एक —— कहलाता है।
(ii) यदि A = {1,2,3}, B = {4,5,6,7} तथा {(1,4)(2,5)(3,6)} ![]() से
से ![]() पर एक फलन है तो
पर एक फलन है तो ![]() एक —— फलन है।
एक —— फलन है।
(iii) ![]() में प्रतिबंध
में प्रतिबंध ![]() तथा
तथा ![]() जहाँ
जहाँ ![]() को संतुष्ट करने वाला सम्बंध
को संतुष्ट करने वाला सम्बंध ![]() —— सम्बंध है।
—— सम्बंध है।
(iv) ![]() में इस प्रकार का सम्बंध
में इस प्रकार का सम्बंध ![]() जो प्रतिबंध
जो प्रतिबंध ![]() का तात्पर्य है कि
का तात्पर्य है कि ![]() को संतुष्ट करता है A —— सम्बंध है।
को संतुष्ट करता है A —— सम्बंध है।
(v) ![]() में ऐसा सम्बंध है कि फॉर ऑल
में ऐसा सम्बंध है कि फॉर ऑल ![]() —— सम्बंध है।
—— सम्बंध है।
(vi) ![]() में
में ![]() द्वारा प्रदत्त सम्बंध
द्वारा प्रदत्त सम्बंध ![]() —— सम्बंध है।
—— सम्बंध है।
(vii) एक फलन ![]() एकैकी फलन है यदि
एकैकी फलन है यदि ![]() तब सभी
तब सभी ![]() के लिए
के लिए ![]()
प्रश्न 3. सत्य/असत्य लिखो :
(i) यदि A = {1,2,3} हो तो ऐसे संबंध जिनमे अवयव (1,2) तथा (1,3) हो और जो स्वतुल्य तथा सममित है किंतु संक्रामक नहीं है की संख्या 1 है
(ii) यदि ![]() तथा
तथा ![]() समुच्चय
समुच्चय ![]() मे तुल्यता संबंध है तो
मे तुल्यता संबंध है तो ![]() भी एक तुल्यता संबंध होगा
भी एक तुल्यता संबंध होगा
(iii) यदि ![]() एक फलन है
एक फलन है ![]() में
में ![]() द्वारा प्रदत्त एक संबंध है तो
द्वारा प्रदत्त एक संबंध है तो ![]() एक तुल्यता संबंध नहीं है।
एक तुल्यता संबंध नहीं है।
(iv) ![]() एक आच्छादक फलन है यदि और केवल यदि
एक आच्छादक फलन है यदि और केवल यदि ![]() का परिसर =
का परिसर = ![]()
(v) ![]() एकैकी कहलाता है यदि
एकैकी कहलाता है यदि ![]() के लिए
के लिए ![]()
प्रश्न क्रमांक –
- सिद्ध कीजिए कि
 में
में 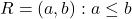 द्वारा परिभाषित संबंध स्वतुल्य तथा संक्रामक है।
द्वारा परिभाषित संबंध स्वतुल्य तथा संक्रामक है। - यदि
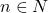 के लिए
के लिए 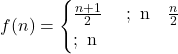 द्वारा परिभाषित एक फलन
द्वारा परिभाषित एक फलन 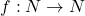 है तो दिखाइए कि
है तो दिखाइए कि  एकैकी आच्छादक है।
एकैकी आच्छादक है। - जाँच कीजिए कि क्या समुच्चय {1,2,3,4,5,6} में R = {(a,b): b = a + 1} द्वारा परिभाषित संबंध
 एक तुल्यता संबंध है।
एक तुल्यता संबंध है। - सिद्ध कीजिए कि पूर्णांको के समुच्चय R = (a,b) ‘संख्या 2, (a-b) को विभाजित करती है’ द्वारा प्रदत्त संबंध एक तुल्यता संबंध है।
- यदि फलन
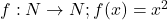 द्वारा प्रदत्त फलन की एकैकी तथा आच्छादी गुणों की जाँच कीजिए।
द्वारा प्रदत्त फलन की एकैकी तथा आच्छादी गुणों की जाँच कीजिए। - यदि A = {1,2,3}, B = {4,5,6,7} तथा f = {(1,4)(2,5)(3,6)}
 से
से  पर एक फलन है तो दिखाइए कि
पर एक फलन है तो दिखाइए कि  एकैकी है।
एकैकी है। - सिद्ध कीजिए कि समुच्चय {1,2,3} में R = {(1,2)(2,1)} द्वारा प्रदत्त संबंध
 सममित है।
सममित है। - सिद्ध कीजिए कि f(1)=f(2)=1 तथा x>2 के लिए f(x)=x-1 द्वारा प्रदत्त फलन
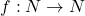 आच्छादक तो है किन्तु एकैकी नहीं है।
आच्छादक तो है किन्तु एकैकी नहीं है। - सिद्ध कीजिए कि किसी कॉलेज के पुस्तकालय की समस्त पुस्तकों के समुच्चय
 में
में 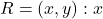 तथा
तथा  में पेजों की संख्या समान है} द्वारा प्रदत्त संबंध
में पेजों की संख्या समान है} द्वारा प्रदत्त संबंध  एक तुल्यता संबंध है।
एक तुल्यता संबंध है। - सिद्ध कीजिए कि A = {1,2,3,4,5} में, R = {(a,b): |a-b| सम है} द्वारा प्रदत्त संबंध
 एक तुल्यता संबंध है। प्रमाणित कीजिए कि {1,3,5} के सभी अवयव एक दूसरे से संबंधित हैं और समुच्चय {2,4} के सभी अवयव एक दूसरे से संबंधित हैं परंतु {1,3,5} का कोई भी अवयव {2,4} के किसी अवयव से संबंधित नहीं है।
एक तुल्यता संबंध है। प्रमाणित कीजिए कि {1,3,5} के सभी अवयव एक दूसरे से संबंधित हैं और समुच्चय {2,4} के सभी अवयव एक दूसरे से संबंधित हैं परंतु {1,3,5} का कोई भी अवयव {2,4} के किसी अवयव से संबंधित नहीं है। - सिद्ध कीजिए कि
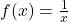 द्वारा परिभाषित फलन
द्वारा परिभाषित फलन 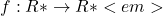 एकैकी तथा आच्छादक है, जहाँ
एकैकी तथा आच्छादक है, जहाँ 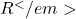 सभी ऋणेतर वास्तविक संख्याओं का समुच्चय है। यदि प्रांत
सभी ऋणेतर वास्तविक संख्याओं का समुच्चय है। यदि प्रांत 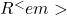 को
को 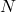 से बदल दिया जाए, जब कि सहप्रांत पूर्ववत
से बदल दिया जाए, जब कि सहप्रांत पूर्ववत 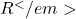 ही रहे, तो भी क्या यह परिणाम सत्य होगा?
ही रहे, तो भी क्या यह परिणाम सत्य होगा? - सिद्ध कीजिए कि समस्त बहुभुजों के समुच्चय
 में,
में, 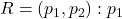 तथा
तथा 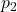 की भुजाओं की संख्या समान है} प्रकार से परिभाषित संबंध
की भुजाओं की संख्या समान है} प्रकार से परिभाषित संबंध  एक तुल्यता संबंध है। 3, 4, और 5 लंबाई की भुजाओं वाले समकोण त्रिभुज से संबंधित समुच्चय
एक तुल्यता संबंध है। 3, 4, और 5 लंबाई की भुजाओं वाले समकोण त्रिभुज से संबंधित समुच्चय  के सभी अवयवों का समुच्चय ज्ञात कीजिए।
के सभी अवयवों का समुच्चय ज्ञात कीजिए।
उत्तर- (अध्याय 1)
प्रश्न 1. (i) b (ii) a (iii) b (iv) b (v) d (vi) d (vii) c (viii) c (ix) d (x) b (xi) b (xii) c (xiii) b (xiv) a (xv) c (xvi) b (xvii) c (xviii) b (xix) c (xx) a (xxi) c (xxii) a (xxiii) a (xxiv) a
प्रश्न 2. (i) तुल्यता संबंध (ii) एकैकी (iii) संक्रामक (iv) सममित सम्बंध (v) स्वतुल्य सम्बंध (vi) सार्वत्रिक सम्बंध (vii) ![]()
प्रश्न 3. (i) सत्य (ii) सत्य (iii) असत्य (iv) सत्य (v) असत्य