MP Board 12th Mathematics Quarterly Exam 2025-26 Question Bank : इस MP Board 12th Mathematics Quarterly Exam 2025-26 Question Bank से ब्लूप्रिंट के अनुरूप प्रश्न पत्र के आधार पर छात्र अपनी तैयारी कर सकते हैं ।

त्रैमासिक परीक्षा 2025-26
कक्षा : 12वीं
विषय : गणित
पूर्णांक : 80 समय : 3:00 घंटे
नोट:
प्रश्न कमांक 1 से 5 तक 32 वस्तुनिष्ठ प्रश्न होंगे, प्रत्येक प्रश्न पर एक अंक निर्धारित है। प्रश्न निम्नलिखित रहेगा –
प्रश्न कमांक 1 – सभी विकल्प 06,
प्रश्न कमांक 2 – रिक्त स्थान 06,
प्रश्न कमांक 3 – सत्य/असत्य 06,
प्रश्न कमांक 4 – सभी-जोड़ी 07,
प्रश्न कमांक 5 – एक वाक्यम में उत्तर 07,
प्रश्न कमांक – 6 से 15 तक कुल 10 प्रश्न होंगे, प्रत्येक प्रश्न पर 02 अंक निर्धारित है।
प्रश्न कमांक – 16 से 19 तक कुल 04 प्रश्न होंगे, प्रत्येक प्रश्न पर 03 अंक निर्धारित है।
प्रश्न कमांक – 20 से 23 तक कुल 04 प्रश्न होंगे, प्रत्येक प्रश्न पर 04 अंक निर्धारित है।
Chapter 3 : Matrices (आव्यूह) से संबन्धित प्रश्न देखने के लिए यहाँ क्लिक करें
Chapater 4 : Determinant (सारणिक) से संबन्धित प्रश्न देखने के लिए यहाँ क्लिक करें
अध्याय 1 संबंध एवं फलन
प्रश्न 1. सही विकल्प चुनिए –
- यदि समुच्चय
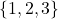 में
में 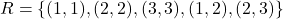 द्वारा प्रदत्त संबंध है :
द्वारा प्रदत्त संबंध है : - यदि फलन
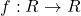 जो
जो 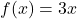 द्वारा परिभाषित है तो फलन
द्वारा परिभाषित है तो फलन  :
: - यदि फलन
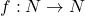 जो
जो 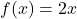 द्वारा परिभाषित है तो फलन
द्वारा परिभाषित है तो फलन  :
: - यदि समुच्चय
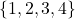 में
में 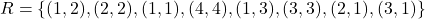 द्वारा प्रदत्त संबंध है तो :
द्वारा प्रदत्त संबंध है तो : - यदि
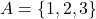 हो निम्न में से कौन सा तुल्यता संबंध नहीं है:
हो निम्न में से कौन सा तुल्यता संबंध नहीं है: - माना समुच्चय
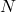 में
में 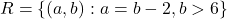 द्वारा प्रदत्त संबंध है तब निम्न में से सही उत्तर चुनिए:
द्वारा प्रदत्त संबंध है तब निम्न में से सही उत्तर चुनिए: - दिए गए समुच्चय
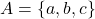 के लिए एक तत्समक संबंध होगा:
के लिए एक तत्समक संबंध होगा: - माना
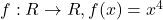 द्वारा परिभाषित है तो :
द्वारा परिभाषित है तो : - माना
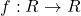 , इस प्रकार परिभाषित है कि
, इस प्रकार परिभाषित है कि 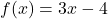 तब
तब 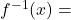
- माना
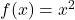 और
और 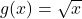 तब :
तब : - माना
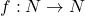 इस प्रकार परिभाषित है कि
इस प्रकार परिभाषित है कि 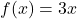 जहाँ
जहाँ 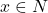 तब
तब  होगा:
होगा: - यदि
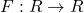 जहाँ
जहाँ 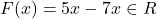 तब
तब 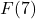 का मान होगा:
का मान होगा: - माना समुच्चय
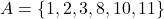 और
और  समुच्चय
समुच्चय  पर परिभाषित संबंध इस प्रकार है कि
पर परिभाषित संबंध इस प्रकार है कि 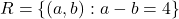 तब संबंध
तब संबंध  होगा:
होगा: - माना
 एक संबंध
एक संबंध 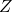 पर इस प्रकार परिभाषित है कि
पर इस प्रकार परिभाषित है कि 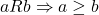 तब
तब  होगा
होगा - माना
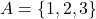 ,
, 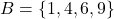 और संबंध
और संबंध  से
से  पर इस प्रकार है कि
पर इस प्रकार है कि  बड़ा है
बड़ा है  से तब
से तब  का परिसर क्या होगा?
का परिसर क्या होगा? - यदि समुच्चय
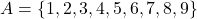 पर संबंध
पर संबंध  इस प्रकार परिभाषित है कि
इस प्रकार परिभाषित है कि 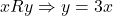 तब
तब  बराबर है:
बराबर है: - यदि
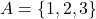 हो तो अवयव
हो तो अवयव 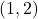 वाले तुल्यता संबंधों की संख्या है-
वाले तुल्यता संबंधों की संख्या है- - यदि
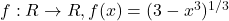 द्वारा प्रदत्त है तो
द्वारा प्रदत्त है तो 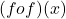 का मान क्या होगा:
का मान क्या होगा: - यदि
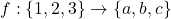 इस प्रकार हो कि
इस प्रकार हो कि 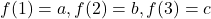 तब
तब 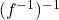 है:
है: - यदि
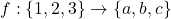 इस प्रकार हो कि
इस प्रकार हो कि 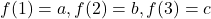 तब
तब 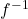 है:
है: - यदि
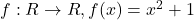 जहाँ
जहाँ 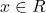 द्वारा परिभाषित है तो
द्वारा परिभाषित है तो 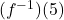 का मान है:
का मान है: 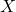 में प्रतिबंध
में प्रतिबंध  ,
, 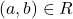 तथा
तथा 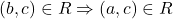 जहाँ
जहाँ 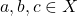 को सन्तुष्ट करने वाला संबंध
को सन्तुष्ट करने वाला संबंध  :
:- प्रदत्त संबंध
 रिक्त संबंध होगा यदि –
रिक्त संबंध होगा यदि – 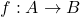 एक आच्छादक फलन होगा यदि
एक आच्छादक फलन होगा यदि- यदि
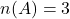 तथा
तथा 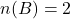 तो
तो 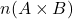 बराबर है:
बराबर है: 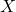 में संबंध
में संबंध  जो स्वतुल्य सममित तथा संक्रामक है वह संबंध कहलाता है –
जो स्वतुल्य सममित तथा संक्रामक है वह संबंध कहलाता है –- यदि
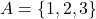 हो तो ऐसे सम्बन्ध जिनमें अवयव
हो तो ऐसे सम्बन्ध जिनमें अवयव 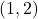 तथा
तथा 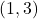 हों और जो स्वतुल्य तथा सममित हैं किन्तु संक्रामक नहीं हैं, की संख्या है :
हों और जो स्वतुल्य तथा सममित हैं किन्तु संक्रामक नहीं हैं, की संख्या है :
(a) केवल सममित (b) केवल स्वतुल्य (c) केवल संक्रामक (d) एक तुल्यता संबंध
(a) एकैकी आच्छादक है (b) एकैकी है किन्तु आच्छादक नहीं है। (c) आच्छादक है किन्तु एकैकी नहीं (d) एकैकी आच्छादक दोनों नहीं है।
(a) एकैकी आच्छादक है। (b) एकैकी है किन्तु आच्छादक नहीं है। (c) आच्छादक है किन्तु एकैकी नहीं (d) एकैकी आच्छादक दोनों नहीं है।
(a) स्वतुल्य तथा सममित है किन्तु संक्रामक नहीं है। (b) स्वतुल्य तथा संक्रामक है किन्तु सममित नहीं है। (c) सममित तथा संक्रामक है किन्तु स्वतुल्य नहीं है। (d) एक तुल्यता संबंध है।
(a) ![]() (b)
(b) ![]() (c)
(c) ![]() (d) इनमें से कोई नहीं
(d) इनमें से कोई नहीं
(a) ![]() (b)
(b) ![]() (c)
(c) ![]() (d)
(d) ![]()
(a) ![]() (b)
(b) ![]() (c)
(c) ![]() (d)
(d) ![]()
(a) ![]() एकैकी आच्छादक है।
(b)
एकैकी आच्छादक है।
(b) ![]() बहुएक आच्छादक नहीं है।
(c)
बहुएक आच्छादक नहीं है।
(c) ![]() एकैकी पर आच्छादक नहीं
(d)
एकैकी पर आच्छादक नहीं
(d) ![]() न एकैकी है और न आच्छादक।
न एकैकी है और न आच्छादक।
(a) ![]() (b)
(b) ![]() (c)
(c) ![]() (d) इनमें से कोई नहीं।
(d) इनमें से कोई नहीं।
(a) ![]() (b)
(b) ![]() (c)
(c) ![]() (d) इनमें से कोई नहीं।
(d) इनमें से कोई नहीं।
(a) आच्छादक (b) प्रतिलोम (c) एकैकी (d) इनमें से कोई नहीं
(a) ![]() (b)
(b) ![]() (c)
(c) ![]() (d)
(d) ![]()
(a) रिक्त संबंध (b) स्वतुल्य संबंध (c) सममित संबंध (d) तुल्यता संबंध
(a) सममित संक्रामक किन्तु स्वतुल्य नहीं (b) स्वतुल्य सममित किन्तु संक्रामक नहीं (c) स्वतुल्य और संक्रामक किन्तु सममित नहीं। (d) एक तुल्यता संबंध
(a) ![]() (b)
(b) ![]() (c)
(c) ![]() (d) इनमें से कोई नहीं
(d) इनमें से कोई नहीं
(a) ![]() (b)
(b) ![]() (c)
(c) ![]() (d) इनमें से कोई नहीं
(d) इनमें से कोई नहीं
(a) ![]() (b)
(b) ![]() (c)
(c) ![]() (d)
(d) ![]()
(a) ![]() (b)
(b) ![]() (c)
(c) ![]() (d)
(d) ![]()
(a) ![]() (b)
(b) ![]() (c)
(c) ![]() (d)
(d) ![]()
(a) ![]() (b)
(b) ![]() (c)
(c) ![]() (d)
(d) ![]()
(a) ![]() (b)
(b) ![]() (c)
(c) ![]() (d) अस्तित्व नहीं है।
(d) अस्तित्व नहीं है।
(a) सममित संबंध है। (b) स्वतुल्य संबंध है। (c) संक्रामक संबंध है। (d) रिक्त संबंध है।
(a) ![]() (b)
(b) ![]() (c)
(c) ![]() (d)
(d) ![]()
(a) ![]() (b)
(b) ![]() (c)
(c) ![]() (d)
(d) ![]()
(a) ![]() (b)
(b) ![]() (c)
(c) ![]() (d)
(d) ![]()
(a) तुल्यता संबंध (b) सार्वत्रिक सम्बंध (c) रिक्त संबंध (d) सममित संबंध
(a) ![]() (b)
(b) ![]() (c)
(c) ![]() (d)
(d) ![]()
प्रश्न 2. रिक्त स्थानों की पूर्ति कीजिए:
- समुच्चय
 पर परिभाषित कोई संबंध
पर परिभाषित कोई संबंध  स्वतुल्य सममित तथा संक्रामक है तो
स्वतुल्य सममित तथा संक्रामक है तो  एक \_________\_ कहलाता है |
एक \_________\_ कहलाता है | - यदि फलन
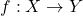 एक व्युत्क्रमणीय फलन है तो फलन अनिवार्यत: एकैकी तथा \_________\_ होता है |
एक व्युत्क्रमणीय फलन है तो फलन अनिवार्यत: एकैकी तथा \_________\_ होता है | - यदि
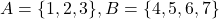 तथा
तथा 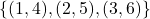
 से
से  पर एक फलन है तो
पर एक फलन है तो  एक\_________\_फलन है |
एक\_________\_फलन है | 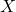 में प्रतिबंध
में प्रतिबंध  ,
, 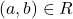 तथा
तथा 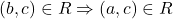 जहाँ
जहाँ 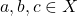 को सन्तुष्ट करने वाला संबंध
को सन्तुष्ट करने वाला संबंध  \_________\_ संबंध है |
\_________\_ संबंध है |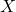 में इस प्रकार का संबंध
में इस प्रकार का संबंध  जो प्रतिबंध
जो प्रतिबंध 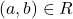 का तात्पर्य है कि
का तात्पर्य है कि 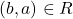 को सन्तुष्ट करता है
को सन्तुष्ट करता है  \_________\_ संबंध है |
\_________\_ संबंध है |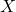 में ऐसा संबंध है कि फॉर ऑल
में ऐसा संबंध है कि फॉर ऑल 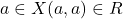 \_________\_ संबंध है |
\_________\_ संबंध है |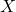 में
में 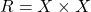 द्वारा प्रदत्त संबंध
द्वारा प्रदत्त संबंध  \_________\_ संबंध है |
\_________\_ संबंध है |- एक फलन
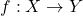 एकैकी फलन है यदि
एकैकी फलन है यदि 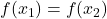 तब सभी
तब सभी 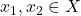 के लिए
के लिए  हो तो ऐसे संबंध जिनमें अवयव
हो तो ऐसे संबंध जिनमें अवयव 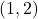 तथा
तथा 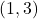 हो और जो स्वतुल्य तथा सममित है किन्तु संक्रामक नहीं है की संख्या
हो और जो स्वतुल्य तथा सममित है किन्तु संक्रामक नहीं है की संख्या 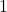 है |
है | - यदि
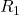 तथा
तथा 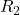 समुच्चय
समुच्चय  में तुल्यता संबंध है तो
में तुल्यता संबंध है तो 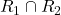 भी एक तुल्यता संबंध होगा |
भी एक तुल्यता संबंध होगा | - यदि
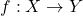 एक फलन है
एक फलन है 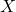 में
में 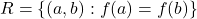 द्वारा प्रदत्त एक संबंध है तो
द्वारा प्रदत्त एक संबंध है तो  एक तुल्यता संबंध नहीं है |
एक तुल्यता संबंध नहीं है | 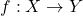 आच्छादक फलन है यदि और केवल यदि
आच्छादक फलन है यदि और केवल यदि  का परिसर
का परिसर 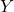 |
|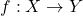 एकैकी कहलाता है यदि
एकैकी कहलाता है यदि 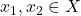 के लिए
के लिए 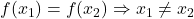 |
|
2 अंकीय प्रश्न:
- रिक्त सम्बन्ध को परिभाषित कीजिए |
- सार्वत्रिक सम्बन्ध क्या कहलाता है?
- सिद्ध कीजिए कि
 में
में 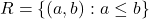 द्वारा परिभाषित संबंध स्वतुल्य तथा संक्रामक है |
द्वारा परिभाषित संबंध स्वतुल्य तथा संक्रामक है | - सिद्ध कीजिए कि यदि
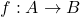 तथा
तथा 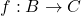 एकैकी है तो
एकैकी है तो 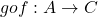 भी एकैकी है |
भी एकैकी है | - सिद्ध कीजिए कि
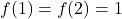 तथा
तथा 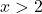 के लिए
के लिए 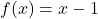 द्वारा प्रदत्त फलन
द्वारा प्रदत्त फलन 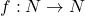 आच्छादक तो है किन्तु एकैकी नहीं है |
आच्छादक तो है किन्तु एकैकी नहीं है | 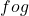 तथा
तथा 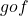 ज्ञात कीजिए यदि
ज्ञात कीजिए यदि 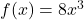 तथा
तथा 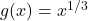 |
|- यदि फलन
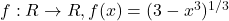 द्वारा प्रदत्त है तो
द्वारा प्रदत्त है तो 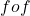 का मान ज्ञात कीजिए |
का मान ज्ञात कीजिए | - यदि फलन
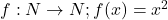 द्वारा प्रदत्त फलन की एकैकी तथा आच्छादी गुणों की जाँच कीजिए |
द्वारा प्रदत्त फलन की एकैकी तथा आच्छादी गुणों की जाँच कीजिए | - यदि
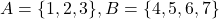 तथा
तथा 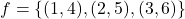
 से
से  पर एक फलन है तो दिखाइए कि
पर एक फलन है तो दिखाइए कि  एकैकी है |
एकैकी है | - सिद्ध कीजिए कि समुच्चय
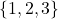 में
में 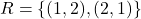 द्वारा प्रदत्त संबंध
द्वारा प्रदत्त संबंध  सममित है |
सममित है | 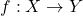 के एकैकी (One-one) होने को परिभाषित कीजिए |
के एकैकी (One-one) होने को परिभाषित कीजिए |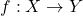 आच्छादक होने की आवश्यक शर्त लिखिए |
आच्छादक होने की आवश्यक शर्त लिखिए |
3 अंकीय प्रश्न:
- तुल्यता संबंध को परिभाषित कीजिए |
- यदि
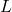 किसी समतल में स्थित समस्त रेखाओं का एक समुच्चय है तथा
किसी समतल में स्थित समस्त रेखाओं का एक समुच्चय है तथा 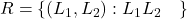 समुच्चय
समुच्चय 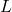 पर परिभाषित एक सम्बन्ध है | सिद्ध कीजिए कि
पर परिभाषित एक सम्बन्ध है | सिद्ध कीजिए कि  सममित है किन्तु न तो स्वतुल्य है न संक्रामक है |
सममित है किन्तु न तो स्वतुल्य है न संक्रामक है | - यदि
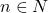 के लिए
के लिए 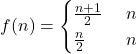 द्वारा परिभाषित एक फलन
द्वारा परिभाषित एक फलन 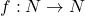 है तो दिखाइए कि
है तो दिखाइए कि  एकैकी आच्छादक है |
एकैकी आच्छादक है | - यदि
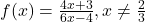 में सिद्ध कीजिए कि
में सिद्ध कीजिए कि 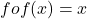 |
| - यदि
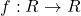 जहाँ
जहाँ 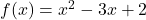 द्वारा परिभाषित है तो
द्वारा परिभाषित है तो 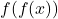 ज्ञात कीजिए |
ज्ञात कीजिए | - मान लीजिए कि
 और
और 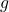 दो फलन इस प्रकार हैं कि
दो फलन इस प्रकार हैं कि 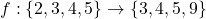 और
और 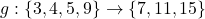 तो
तो 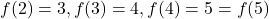 तथा
तथा 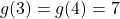 एवं
एवं 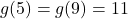 तो
तो 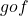 ज्ञात कीजिए |
ज्ञात कीजिए | - यदि
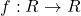 तथा
तथा 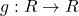 फलन
फलन 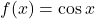 तथा
तथा 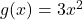 द्वारा परिभाषित है तो
द्वारा परिभाषित है तो 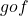 और
और 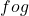 ज्ञात कीजिए | तथा सिद्ध कीजिए
ज्ञात कीजिए | तथा सिद्ध कीजिए 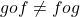 |
|
4 अंकीय प्रश्न:
- जाँच कीजिए कि क्या समुच्चय
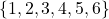 में
में 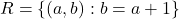 द्वारा परिभाषित संबंध
द्वारा परिभाषित संबंध  एक तुल्यता संबंध है |
एक तुल्यता संबंध है | - सिद्ध कीजिए कि पूर्णांकों के समुच्चय
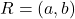 संख्या
संख्या 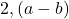 को विभाजित करती है द्वारा प्रदत्त एक तुल्यता संबंध है |
को विभाजित करती है द्वारा प्रदत्त एक तुल्यता संबंध है | - यदि
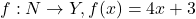 द्वारा परिभाषित एक फलन है, जहाँ
द्वारा परिभाषित एक फलन है, जहाँ 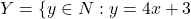 किसी
किसी 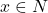 के लिए}\) | सिद्ध कीजिए कि
के लिए}\) | सिद्ध कीजिए कि  व्युत्क्रमणीय है |
व्युत्क्रमणीय है |  का प्रतिलोम फलन ज्ञात कीजिए |
का प्रतिलोम फलन ज्ञात कीजिए | - फलन
![Rendered by QuickLaTeX.com f:[0, \frac{\pi}{2}] \rightarrow R](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-cac1358dd5957cd933e42be82b255473_l3.png) तथा
तथा 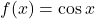 द्वारा प्रदत्त फलन
द्वारा प्रदत्त फलन ![Rendered by QuickLaTeX.com g:[0, \frac{\pi}{2}] \rightarrow R](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-f6876f972413dd33ab937808a3bfdc83_l3.png) पर विचार कीजिए | सिद्ध कीजिए कि
पर विचार कीजिए | सिद्ध कीजिए कि  तथा
तथा 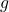 एकैकी है, परन्तु
एकैकी है, परन्तु 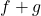 एकैकी नहीं है |
एकैकी नहीं है | - सिद्ध कीजिए कि
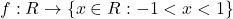 जहाँ
जहाँ 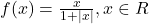 द्वारा परिभाषित फलन एकैकी तथा आच्छादक है |
द्वारा परिभाषित फलन एकैकी तथा आच्छादक है | - यदि
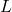 किसी
किसी 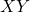 समतल में स्थित समस्त रेखाओं का एक समुच्चय है तथा
समतल में स्थित समस्त रेखाओं का एक समुच्चय है तथा 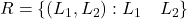 समुच्चय
समुच्चय 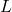 पर परिभाषित एक सम्बन्ध है | सिद्ध कीजिए कि
पर परिभाषित एक सम्बन्ध है | सिद्ध कीजिए कि  एक तुल्यता सम्बन्ध है |
एक तुल्यता सम्बन्ध है | - यदि
 किसी समतल में स्थित समस्त त्रिभुजों का एक समुच्चय है | समुच्चय
किसी समतल में स्थित समस्त त्रिभुजों का एक समुच्चय है | समुच्चय  में
में 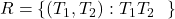 एक सम्बन्ध है | सिद्ध कीजिए कि
एक सम्बन्ध है | सिद्ध कीजिए कि  एक तुल्यता सम्बन्ध है |
एक तुल्यता सम्बन्ध है | - यदि
 किसी समतल में स्थित समस्त त्रिभुजों का एक समुच्चय है | समुच्चय
किसी समतल में स्थित समस्त त्रिभुजों का एक समुच्चय है | समुच्चय  में
में 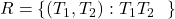 एक सम्बन्ध है | सिद्ध कीजिए कि
एक सम्बन्ध है | सिद्ध कीजिए कि  एक तुल्यता सम्बन्ध है |
एक तुल्यता सम्बन्ध है |
अध्याय-2: प्रतिलोम त्रिकोणमितीय फलन
प्रश्न 1. सही विकल्प चुनिए:
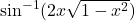 बराबर है :
बराबर है :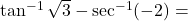
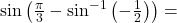
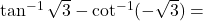
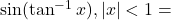
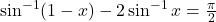 , तब
, तब 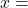
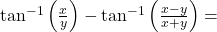
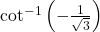 का मुख्य मान होता है :
का मुख्य मान होता है :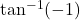 का मुख्य मान है :
का मुख्य मान है :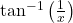 बराबर है :
बराबर है :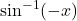 बराबर है :
बराबर है :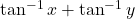 बराबर है :
बराबर है :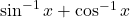 बराबर है :
बराबर है :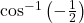 का मान होता है :
का मान होता है :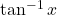 की मुख्य शाखा का परिसर होता है :
की मुख्य शाखा का परिसर होता है :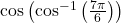 का मान होता है :
का मान होता है :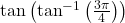 का मान होता है :
का मान होता है :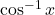 का प्रांत है :
का प्रांत है :
(a) ![]() (b)
(b) ![]() (c)
(c) ![]() (d)
(d) ![]()
(a) ![]() (b)
(b) ![]() (c)
(c) ![]() (d)
(d) ![]()
(a) ![]() (b)
(b) ![]() (c)
(c) ![]() (d)
(d) ![]()
(a) ![]() (b)
(b) ![]() (c)
(c) ![]() (d)
(d) ![]()
(a) ![]() (b)
(b) ![]() (c)
(c) ![]() (d)
(d) ![]()
(a) ![]() (b)
(b) ![]() (c)
(c) ![]() (d)
(d) ![]()
(a) ![]() (b)
(b) ![]() (c)
(c) ![]() (d)
(d) ![]()
(a) ![]() (b)
(b) ![]() (c)
(c) ![]() (d)
(d) ![]()
(a) ![]() (b)
(b) ![]() (c)
(c) ![]() (d)
(d) ![]()
(a) ![]() (b)
(b) ![]() (c)
(c) ![]() (d)
(d) ![]()
(a) ![]() (b)
(b) ![]() (c)
(c) ![]() (d)
(d) ![]()
(a) ![]() (b)
(b) ![]() (c)
(c) ![]() (d)
(d) ![]()
(a) ![]() (b)
(b) ![]() (c)
(c) ![]() (d)
(d) ![]()
(a) ![]() (b)
(b) ![]() (c)
(c) ![]() (d)
(d) ![]()
(a) ![]() (b)
(b) ![]() (c)
(c) ![]() (d)
(d) ![]()
(a) ![]() (b)
(b) ![]() (c)
(c) ![]() (d)
(d) ![]()
(a) ![]() (b)
(b) ![]() (c)
(c) ![]() (d)
(d) ![]()
(a) ![]() (b)
(b) ![]() (c)
(c) ![]() (d)
(d) ![]()
प्रश्न 2. रिक्त स्थानों की पूर्ति कीजिए:
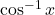 का प्रांत \_________\_ है |
का प्रांत \_________\_ है |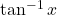 की मुख्य मान शाखा \_________\_ है |
की मुख्य मान शाखा \_________\_ है |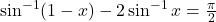 हो तो
हो तो 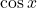 का मान \_________\_ है |
का मान \_________\_ है |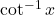 की मुख्य शाखा का परिसर \_________\_ है |
की मुख्य शाखा का परिसर \_________\_ है |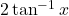 बराबर \_________\_ है |
बराबर \_________\_ है |- किसी प्रतिलोम त्रिकोणमितीय फलन का मुख्य मान वह मान होता है जो उसकी \_________\_ में स्थित होता है |
प्रश्न 3. सत्य/असत्य लिखिए:
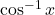 का प्रांत
का प्रांत 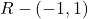 है |
है |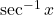 की मुख्य मान शाखा
की मुख्य मान शाखा ![Rendered by QuickLaTeX.com [0, \pi] - \{\frac{\pi}{2}\}](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-9822e2db7200a4266f4d2b14b0ea7f47_l3.png) है |
है |- किसी प्रतिलोम त्रिकोणमितीय फलन का मुख्य मान वह मान होता है जो उसकी मुख्य शाखा में स्थित नहीं होता है |
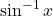 का प्रांत
का प्रांत ![Rendered by QuickLaTeX.com [-1, 1]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-61888feeeeb8e122a17b229740cd3b65_l3.png) है |
है |- यदि
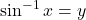 तब
तब 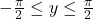 है |
है | 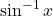 और
और 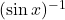 दोनों समान हैं |
दोनों समान हैं |
प्रश्न 3. एक शब्द/वाक्य में उत्तर दीजिए |
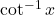 का प्रांत लिखिए |
का प्रांत लिखिए |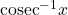 की मुख्य मान शाखा लिखिए |
की मुख्य मान शाखा लिखिए |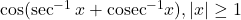 का मान लिखिए |
का मान लिखिए |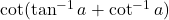 का मान लिखिए |
का मान लिखिए |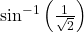 का मुख्य मान क्या होता है ?
का मुख्य मान क्या होता है ?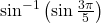 का मान क्या होता है :
का मान क्या होता है :
2 अंकीय प्रश्न:
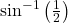 का मुख्य मान ज्ञात कीजिए |
का मुख्य मान ज्ञात कीजिए |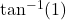 का मुख्य मान ज्ञात कीजिए |
का मुख्य मान ज्ञात कीजिए |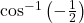 का मुख्य मान ज्ञात कीजिए |
का मुख्य मान ज्ञात कीजिए |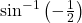 का मुख्य मान ज्ञात कीजिए |
का मुख्य मान ज्ञात कीजिए |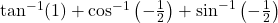 का मान ज्ञात कीजिए |
का मान ज्ञात कीजिए |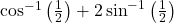 का मान ज्ञात कीजिए |
का मान ज्ञात कीजिए |- दर्शाइए कि
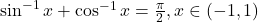
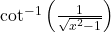 को सरलतम रूप में लिखिए |
को सरलतम रूप में लिखिए |- मान ज्ञात कीजिए:
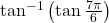
- मान ज्ञात कीजिए:
![Rendered by QuickLaTeX.com \tan^{-1}\left[2\cos\left(2\sin^{-1}\frac{1}{2}\right)\right]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-0612a0e84f980ee49cd4351a60a0bb69_l3.png)
3 अंकीय प्रश्न:
- दर्शाइए कि
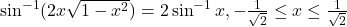 |
| - दर्शाइए कि
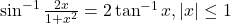 |
| - सिद्ध कीजिए कि
![Rendered by QuickLaTeX.com 3\sin^{-1}x = \sin^{-1}(3x - 4x^3), x \in [-\frac{1}{2}, \frac{1}{2}]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-9698fbe29d8f45db27d334b63e8accee_l3.png) |
| - सिद्ध कीजिए कि
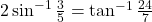 |
| - सिद्ध कीजिए कि
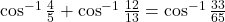 |
| 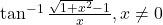 का सरलतम रूप में लिखिए |
का सरलतम रूप में लिखिए |- सिद्ध कीजिए कि
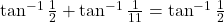 |
| 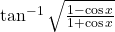 का सरलतम रूप में लिखिए |
का सरलतम रूप में लिखिए |- दर्शाइए कि
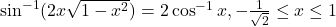 |
| - सिद्ध कीजिए कि
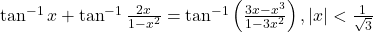 |
| - सिद्ध कीजिए कि
![Rendered by QuickLaTeX.com 3\sin^{-1}x = \sin^{-1}(3x - 4x^3), x \in [-\frac{1}{2}, \frac{1}{2}]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-9698fbe29d8f45db27d334b63e8accee_l3.png) |
| - सिद्ध कीजिए कि
![Rendered by QuickLaTeX.com 3\cos^{-1}x = \cos^{-1}(4x^3 - 3x), x \in [\frac{1}{2}, 1]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-53ab21847edbbeb68a630a4c4f5857ce_l3.png) |
| - सिद्ध कीजिए कि
![Rendered by QuickLaTeX.com \tan^{-1}\sqrt{x} = \frac{1}{2}\cos^{-1}\left(\frac{1-x}{1+x}\right), x \in [0, 1]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-d93582d6bfc8ddc9b4f3304f2ea530e7_l3.png) |
| - सिद्ध कीजिए कि
![Rendered by QuickLaTeX.com \tan^{-1}\left[\frac{\sqrt{1+x}-\sqrt{1-x}}{\sqrt{1+x}+\sqrt{1-x}}\right] = \frac{\pi}{4} - \frac{1}{2}\cos^{-1}x, -\frac{1}{\sqrt{2}} \leq x \leq 1](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-f751aebc20478fcdaf15a06c6993c8a1_l3.png) |
| 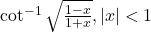 को सरलतम रूप में लिखिए |
को सरलतम रूप में लिखिए |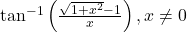 को सरलतम रूप में लिखिए |
को सरलतम रूप में लिखिए |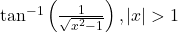 को सरलतम रूप में लिखिए |
को सरलतम रूप में लिखिए |![Rendered by QuickLaTeX.com \tan^{-1}\left[\frac{\sqrt{a^2-x^2}}{x}\right], |x| < 1](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-324261ba2ab22e1e0286d7a830e8f07f_l3.png) को सरलतम रूप में लिखिए |
को सरलतम रूप में लिखिए |![Rendered by QuickLaTeX.com \tan^{-1}\left[\frac{\cos x}{1-\sin x}\right], -\frac{\pi}{2} < x < \frac{3\pi}{2}](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-bf67ab3e8c1388d59be1792dc17a97fc_l3.png) को सरलतम रूप में लिखिए |
को सरलतम रूप में लिखिए |![Rendered by QuickLaTeX.com \tan^{-1}\left[\sqrt{\frac{1-\cos x}{1+\cos x}}\right], x < \pi](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-4ae91db581957cc66ff9ccc211a4346e_l3.png) को सरलतम रूप में लिखिए |
को सरलतम रूप में लिखिए |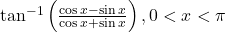 को सरलतम रूप में लिखिए |
को सरलतम रूप में लिखिए |- सिद्ध कीजिए
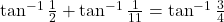 |
| 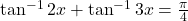 को सरल कीजिए |
को सरल कीजिए |- दर्शाइए कि
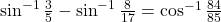 |
| - सिद्ध कीजिए
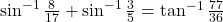 |
| - सिद्ध कीजिए
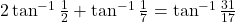 |
| - दर्शाइए कि
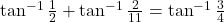 |
| - सिद्ध कीजिए
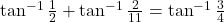 |
| - सिद्ध कीजिए
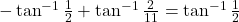 |
| - सिद्ध कीजिए
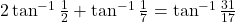 |
| ![Rendered by QuickLaTeX.com \tan\left[2\cos\left(2\sin^{-1}\frac{1}{2}\right)\right]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-24d35625d4c2b20d7d74ee7291b876bd_l3.png) का मान ज्ञात कीजिए |
का मान ज्ञात कीजिए |- यदि
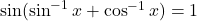 है तो
है तो  का मान ज्ञात कीजिए |
का मान ज्ञात कीजिए | - हल कीजिए
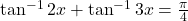 |
| ![Rendered by QuickLaTeX.com \sin^{-1}\left[\sin\frac{2\pi}{3}\right]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-447080fc123f092a9437791ed73ef2ff_l3.png) का मान ज्ञात कीजिए |
का मान ज्ञात कीजिए |![Rendered by QuickLaTeX.com \sin^{-1}\left[\sin\frac{3\pi}{5}\right]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-bb606e317c5794aecf3963324468e6f8_l3.png) का मान ज्ञात कीजिए |
का मान ज्ञात कीजिए |![Rendered by QuickLaTeX.com \tan^{-1}\left[\tan\frac{3\pi}{4}\right]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-4fe5b7ea98635147c37b8fcd65a58f91_l3.png) का मान ज्ञात कीजिए |
का मान ज्ञात कीजिए |![Rendered by QuickLaTeX.com \tan^{-1}\left[\tan\frac{7\pi}{6}\right]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-93b27e72bdf0f3c7ca78db05e72403f4_l3.png) का मान ज्ञात कीजिए |
का मान ज्ञात कीजिए |![Rendered by QuickLaTeX.com \cos^{-1}\left[\cos\frac{13\pi}{6}\right]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-a5b47e6be08fb78aaa19abd1a9f3210c_l3.png) का मान ज्ञात कीजिए |
का मान ज्ञात कीजिए |![Rendered by QuickLaTeX.com \tan\left[\sin^{-1}\frac{3}{5} + \cot^{-1}\frac{3}{2}\right]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-8a75a03c532e912c1b6334ee030c0e44_l3.png) का मान ज्ञात कीजिए |
का मान ज्ञात कीजिए |- दर्शाइए कि
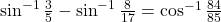 |
| - दर्शाइए कि
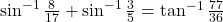 |
| - दर्शाइए कि
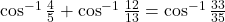 |
|
4 अंकीय प्रश्न:
- फलन
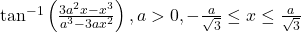 को सरलतम रूप में लिखिए |
को सरलतम रूप में लिखिए | - सरल कीजिए
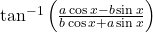 , if
, if 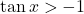 |
| - सिद्ध कीजिए
![Rendered by QuickLaTeX.com \tan^{-1}\left[\frac{\sqrt{1+\sin x}+\sqrt{1-\sin x}}{\sqrt{1+\sin x}-\sqrt{1-\sin x}}\right] = \frac{x}{2}, x \in [0, \frac{\pi}{4}]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-12d491fda0a587d3365df4bdcdcc7039_l3.png) |
| - मान ज्ञात कीजिए:
![Rendered by QuickLaTeX.com \tan\left[\frac{1}{2}\sin^{-1}\frac{2x}{1+x^2} + \frac{1}{2}\cos^{-1}\frac{1-y^2}{1+y^2}\right], |x| < 1, y > 0 \text{ और } xy < 1](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-a18050b558924a96a2efaec7f9b7f8f6_l3.png) |
| - यदि
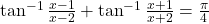 तो
तो  का मान ज्ञात कीजिए |
का मान ज्ञात कीजिए | 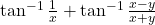 का मान ज्ञात कीजिए |
का मान ज्ञात कीजिए |![Rendered by QuickLaTeX.com \tan^{-1}\left[\frac{\sqrt{1+\sin x}+\sqrt{1-\sin x}}{\sqrt{1+\sin x}-\sqrt{1-\sin x}}\right] = \frac{x}{2}, x \in [0, \frac{\pi}{4}]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-12d491fda0a587d3365df4bdcdcc7039_l3.png) को हल कीजिए |
को हल कीजिए |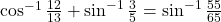 का मान ज्ञात कीजिए |
का मान ज्ञात कीजिए |- हल कीजिए
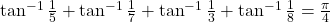 |
|
Remaining Coming Soon
Chapter 3 , Matrices
Chapater 4 Determinant
Chapter5 Continuity and Differentiation
Chapter 6 Differential Applications