MP Board 12th mathematics Matrices Determinent Quarterly Exam 2025-26 Question Bank : इस लेख मे mp board 12th mathamatics Quarterly Exam 2025-26 Question Bank के Determinent आव्यूह और matrices मेट्रिक्स के प्रश्नो का संग्रह है ।
अध्याय-3
आव्यूह
प्रश्न 1. सही विकल्प चुनिए-
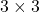 कोटि के ऐसे आव्यूहों की कुल संख्या होगी जिनकी प्रत्येक की प्रविष्टि
कोटि के ऐसे आव्यूहों की कुल संख्या होगी जिनकी प्रत्येक की प्रविष्टि 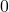 या
या 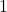 है।
है।![Rendered by QuickLaTeX.com A = [a_{ij}]_{m \times n}](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-23bb136b76df6166d93e2a2bbaf5d0b1_l3.png) एक वर्ग आव्यूह है यदि
एक वर्ग आव्यूह है यदि- आव्यूह
 तथा
तथा  एक दूसरे के व्युत्क्रम होंगे यदि
एक दूसरे के व्युत्क्रम होंगे यदि - यदि एक आव्यूह
 सममित एवं विषम सममित दोनों ही है तो
सममित एवं विषम सममित दोनों ही है तो  :
: - यदि
 तथा
तथा  समान कोटि के सममित आव्यूह है तो
समान कोटि के सममित आव्यूह है तो 
![Rendered by QuickLaTeX.com A = [a_{ij}]_{m \times 1}](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-117b8f01e6d7dba428f4ee2f7990c321_l3.png) एक आव्यूह है।
एक आव्यूह है।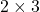 कोटि के आव्यूह में अवयवों की संख्या है।
कोटि के आव्यूह में अवयवों की संख्या है।- यदि
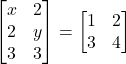 तो
तो  और
और  के मान हैं:
के मान हैं: - आव्यूह
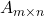 व
व 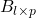 का गुणनफल
का गुणनफल 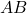 परिभाषित होगा यदि
परिभाषित होगा यदि - एक
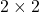 आव्यूह
आव्यूह ![Rendered by QuickLaTeX.com |A| = [a_{ij}]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-3057d3bb8b84cc79a5b30c36f7bd4f71_l3.png) जहाँ
जहाँ 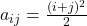 की पहली पंक्ति और दूसरे स्तम्भ का अवयव है।
की पहली पंक्ति और दूसरे स्तम्भ का अवयव है। - यदि आव्यूह
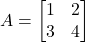 है तो
है तो 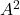 का मान होगा –
का मान होगा –  का मान निम्न के बराबर है।
का मान निम्न के बराबर है।- यदि
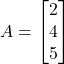
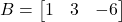 तो
तो 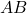 में अवयवों की संख्या होगी-
में अवयवों की संख्या होगी- - निम्n आव्यूह सममित आव्यूह है –
(a) ![]() (b)
(b) ![]() (c)
(c) ![]() (d)
(d) ![]()
(a) ![]() (b)
(b) ![]() (c)
(c) ![]() (d) इनमें से कोई नहीं
(d) इनमें से कोई नहीं
(a) ![]() (b)
(b) ![]() (c)
(c) ![]() (d)
(d) ![]()
(a) एक विकर्ण आव्यूह है (b) एक शून्य आव्यूह है (c) एक वर्ग आव्यूह है (d) इनमें से कोई नहीं
(a) विषम सममित आव्यूह है। (b) सममित आव्यूह है। (c) शून्य आव्यूह है। (d) तत्समक आव्यूह है।
(a) पंक्ति आव्यूह (b) स्तम्भ आव्यूह (c) वर्ग आव्यूह (d) विकर्ण आव्यूह
(a) ![]() (b)
(b) ![]() (c)
(c) ![]() (d)
(d) ![]()
(a) ![]() (b)
(b) ![]() (c)
(c) ![]() (d)
(d) ![]()
(a) ![]() (b)
(b) ![]() (c)
(c) ![]() (d)
(d) ![]()
(a) ![]() (b)
(b) ![]() (c)
(c) ![]() (d)
(d) ![]()
(a) ![]() (b)
(b) ![]() (c)
(c) ![]() (d)
(d) ![]()
(a) ![]() (b)
(b) ![]() (c)
(c) ![]() (d)
(d) ![]()
(a) ![]() (b)
(b) ![]() (c)
(c) ![]() (d)
(d) ![]()
(a) ![]() (b)
(b) ![]() (c)
(c) ![]() (d)
(d) ![]()
प्रश्न 2. सत्य/असत्य लिखिए:
![Rendered by QuickLaTeX.com A = [a_{ij}]_{1 \times n}](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-465f9e1aa4206aa71bef6e9681c0d0d9_l3.png) एक पंक्ति आव्यूह होता है |
एक पंक्ति आव्यूह होता है |- आव्यूहों में योग की संक्रिया के लिए साहचर्य नियम का पालन नहीं होता है।
- किसी
 आव्यूह के लिए
आव्यूह के लिए ![Rendered by QuickLaTeX.com A = [a_{ij}]_{1 \times n}](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-465f9e1aa4206aa71bef6e9681c0d0d9_l3.png) एक स्तम्भ आव्यूह होता है।
एक स्तम्भ आव्यूह होता है। - आव्यूहों में गुणन की संक्रिया के क्रम विनिमेय नियम का पालन नहीं होता है।
- तीन आव्यूहों
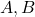 व
व  के लिए
के लिए 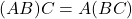
- प्रत्येक वर्ग आव्यूह एक विकर्ण आव्यूह होता है।
- प्रत्येक वर्ग आव्यूह एक अदिश आव्यूह होता है।
- प्रत्येक विकर्ण आव्यूह एक अदिश आव्यूह होता है।
- प्रत्येक अदिश आव्यूह एक विकर्ण आव्यूह होता है।
- प्रत्येक अदिश आव्यूह एक तत्समक आव्यूह होता है।
- प्रत्येक तत्समक आव्यूह एक अदिश आव्यूह होता है।
- प्रत्येक तत्समक आव्यूह एक वर्ग आव्यूह होता है।
- किसी आव्यूह के परिवर्तित आव्यूह का पुन: परिवर्तित आव्यूह मूल आव्यूह के बराबर होता है।
- यदि आव्यूह
 इस प्रकार है कि
इस प्रकार है कि 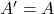 तो आव्यूह
तो आव्यूह  को विषम सममित आव्यूह कहते हैं।
को विषम सममित आव्यूह कहते हैं। - यदि वर्ग आव्यूह
 इस प्रकार है कि
इस प्रकार है कि 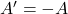 तो
तो  को विषम सममित आव्यूह कहते हैं।
को विषम सममित आव्यूह कहते हैं। - यदि दो वर्ग आव्यूह
 इस प्रकार है कि
इस प्रकार है कि 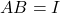 जहाँ
जहाँ  तत्समक आव्यूह है तो आव्यूह
तत्समक आव्यूह है तो आव्यूह  और
और  को एक दूसरे का परिवर्तित आव्यूह कहते हैं।
को एक दूसरे का परिवर्तित आव्यूह कहते हैं। - दो आव्यूहों का योग ज्ञात करने के लिए यह आवश्यक नहीं है कि उनकी कोटियाँ समान हों।
प्रश्न 3. एक शब्द/वाक्य में उत्तर दीजिए :
- यदि
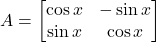 तथा
तथा 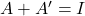 तो
तो  का मान क्या है ?
का मान क्या है ? - यदि
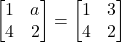 है तो
है तो  का मान क्या है ?
का मान क्या है ? 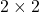 कोटि का तत्समक आव्यूह लिखिए |
कोटि का तत्समक आव्यूह लिखिए |- विकर्ण आव्यूह का कोई एक उदाहरण लिखिए |
- तत्समक आव्यूह को उदाहरण सहित परिभाषित कीजिए |
- विकर्ण आव्यूह क्या है?
- यदि
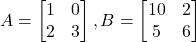 तो
तो 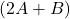 का मान ज्ञात कीजिए |
का मान ज्ञात कीजिए | - आव्यूहों के योग का क्रम विनिमेय नियम लिखिए |
- वर्ग आव्यूह
 को एक सममित आव्यूह और एक विषम सममित आव्यूह के योग के रूप में व्यक्त कीजिए |
को एक सममित आव्यूह और एक विषम सममित आव्यूह के योग के रूप में व्यक्त कीजिए | - यदि
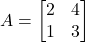 तो
तो 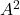 ज्ञात कीजिए |
ज्ञात कीजिए | - पंक्ति आव्यूह को परिभाषित कीजिए |
2 अंकीय प्रश्न
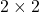 कोटि के आव्यूह
कोटि के आव्यूह ![Rendered by QuickLaTeX.com A = [a_{ij}]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-14896b59c1b535492621540795395abe_l3.png) की रचना कीजिए जिसके अवयव निम्न प्रकार से प्राप्त होते हैं:
की रचना कीजिए जिसके अवयव निम्न प्रकार से प्राप्त होते हैं: 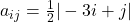
- सरल कीजिए
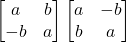
- सरल कीजिए
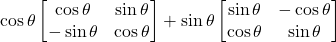
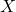 का मान ज्ञात कीजिए, यदि
का मान ज्ञात कीजिए, यदि 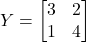 और
और 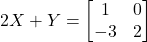
- यदि
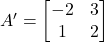 तथा
तथा 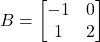 तब
तब 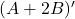 का मान ज्ञात कीजिए |
का मान ज्ञात कीजिए | - यदि
 तथा
तथा 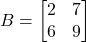 है तो
है तो 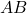 ज्ञात कीजिए |
ज्ञात कीजिए | - यदि
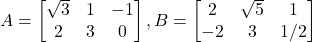 है तो
है तो 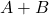 ज्ञात कीजिए |
ज्ञात कीजिए | - यदि
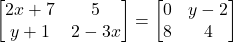 तो
तो  व
व  के मान ज्ञात कीजिए |
के मान ज्ञात कीजिए | 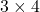 आव्यूह
आव्यूह ![Rendered by QuickLaTeX.com A = [a_{ij}]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-14896b59c1b535492621540795395abe_l3.png) की रचना कीजिए यदि
की रचना कीजिए यदि 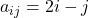
- यदि
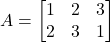 तथा
तथा 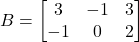 है तो
है तो 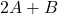 ज्ञात कीजिए |
ज्ञात कीजिए | - आव्यूह
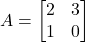 व
व 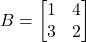 के लिए आव्यूहों के योग के क्रम विनिमेय नियम का सत्यापन कीजिए |
के लिए आव्यूहों के योग के क्रम विनिमेय नियम का सत्यापन कीजिए | 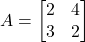 व
व 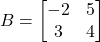 तो
तो  ज्ञात कीजिए |
ज्ञात कीजिए |- आव्यूह
 और
और 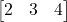 का गुणनफल परिकलित कीजिए |
का गुणनफल परिकलित कीजिए | - यदि
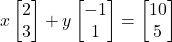 तो
तो  व
व  के मान ज्ञात कीजिए |
के मान ज्ञात कीजिए | - एक
 आव्यूह
आव्यूह ![Rendered by QuickLaTeX.com A = [a_{ij}]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-14896b59c1b535492621540795395abe_l3.png) की रचना कीजिए जबकि
की रचना कीजिए जबकि 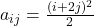
- यदि
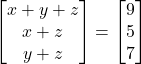 तो
तो 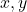 तथा
तथा  के मान ज्ञात कीजिए |
के मान ज्ञात कीजिए |
3 अंकीय प्रश्न:
- यदि
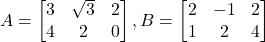 है तो निम्न को सत्यापित कीजिए:
है तो निम्न को सत्यापित कीजिए: 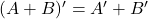
- सत्यापित कीजिए कि
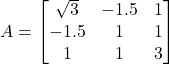 एक सममित आव्यूह है |
एक सममित आव्यूह है | - यदि
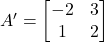 तथा
तथा 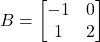 है तो
है तो 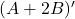 ज्ञात कीजिए |
ज्ञात कीजिए | - यदि
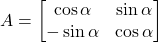 तथा है तो सत्यापित कीजिए
तथा है तो सत्यापित कीजिए 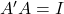
- यदि
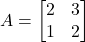 तथा
तथा  तो सिद्ध कीजिए कि दोनों आव्यूह एक दूसरे के व्युत्क्रम हैं |
तो सिद्ध कीजिए कि दोनों आव्यूह एक दूसरे के व्युत्क्रम हैं | - यदि
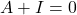 जहाँ
जहाँ  और
और 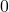 क्रमशः
क्रमशः 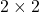 के तत्समक आव्यूह एवं शून्य आव्यूह हैं, तो
के तत्समक आव्यूह एवं शून्य आव्यूह हैं, तो 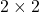 कोटि के आव्यूह
कोटि के आव्यूह  का मान ज्ञात कीजिए |
का मान ज्ञात कीजिए | - यदि
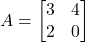 और
और 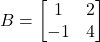 तो सत्यापित कीजिए
तो सत्यापित कीजिए 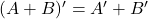
- दिखाइए कि
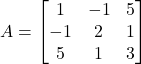 एक सममित आव्यूह है |
एक सममित आव्यूह है | - यदि
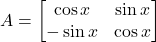 तो सिद्ध कीजिए कि
तो सिद्ध कीजिए कि 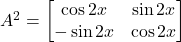
- वर्ग आव्यूह
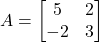 सममित एवं एक विषम सममित आव्यूहों के योग के रूप में व्यक्त कीजिए |
सममित एवं एक विषम सममित आव्यूहों के योग के रूप में व्यक्त कीजिए | - यदि आव्यूह
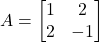 समीकरण
समीकरण 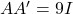 को सन्तुष्ट करता है तो
को सन्तुष्ट करता है तो  व
व  के मान ज्ञात कीजिए | [Note: This question contains a variable x and y that are not present in the given matrix A. Assuming A refers to a different matrix or there’s a typo. The question from the image is “तो x व y के मान ज्ञात कीजिए।”. I am rephrasing for clarity based on what seems to be intended.]
के मान ज्ञात कीजिए | [Note: This question contains a variable x and y that are not present in the given matrix A. Assuming A refers to a different matrix or there’s a typo. The question from the image is “तो x व y के मान ज्ञात कीजिए।”. I am rephrasing for clarity based on what seems to be intended.] - यदि आव्यूह
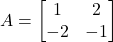 और
और 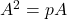 तो
तो  का मान ज्ञात कीजिए |
का मान ज्ञात कीजिए | 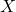 तथा
तथा 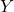 ज्ञात कीजिए यदि
ज्ञात कीजिए यदि 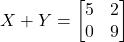 तथा
तथा 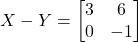
- आव्यूह
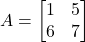 के लिए सत्यापित कीजिए कि
के लिए सत्यापित कीजिए कि 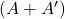 एक सममित तथा
एक सममित तथा 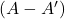 एक विषम सममित आव्यूह है |
एक विषम सममित आव्यूह है | - यदि
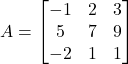 तथा
तथा  है तो सत्यापित कीजिए कि
है तो सत्यापित कीजिए कि 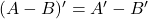
- यदि
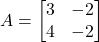 तथा
तथा 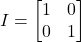 एवं
एवं 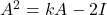 तो
तो  का मान ज्ञात कीजिए |
का मान ज्ञात कीजिए | - दिये गये समीकरण को
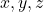 तथा
तथा  के लिए हल कीजिए यदि
के लिए हल कीजिए यदि 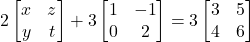
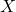 तथा
तथा 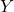 के मान ज्ञात कीजिए यदि
के मान ज्ञात कीजिए यदि 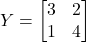 तथा
तथा 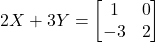
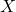 तथा
तथा 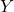 के मान ज्ञात कीजिए यदि
के मान ज्ञात कीजिए यदि 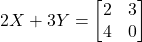 तथा
तथा 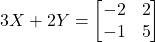
- यदि
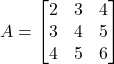 तथा
तथा  हो तो ज्ञात
हो तो ज्ञात 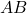 कीजिए |
कीजिए | - यदि
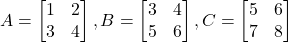 हो तो आव्यूहों के लिए योग के साहचर्य नियम का सत्यापन कीजिए |
हो तो आव्यूहों के लिए योग के साहचर्य नियम का सत्यापन कीजिए |
4 अंकीय प्रश्न:
- यदि
 दिया हो तथा
दिया हो तथा 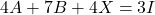 तो आव्यूह
तो आव्यूह 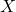 ज्ञात कीजिए | [Note: This equation seems to have a typo for ‘I’ as ‘A’ and ‘B’ are not square matrices, making ‘I’ incompatible for addition/subtraction. Assuming ‘I’ should be a compatible zero matrix or the problem context implies a different setup. I am writing it as it is in the image, but this point might require clarification if it causes issues.]
ज्ञात कीजिए | [Note: This equation seems to have a typo for ‘I’ as ‘A’ and ‘B’ are not square matrices, making ‘I’ incompatible for addition/subtraction. Assuming ‘I’ should be a compatible zero matrix or the problem context implies a different setup. I am writing it as it is in the image, but this point might require clarification if it causes issues.] - यदि
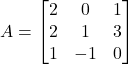 है तो
है तो 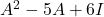 का मान ज्ञात कीजिए |
का मान ज्ञात कीजिए | - आव्यूह
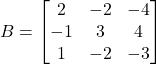 को एक सममित एवं एक विषम सममित आव्यूहों के योग के रूप में व्यक्त कीजिए |
को एक सममित एवं एक विषम सममित आव्यूहों के योग के रूप में व्यक्त कीजिए | - यदि
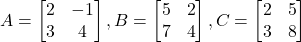 हो तो एक ऐसा आव्यूह
हो तो एक ऐसा आव्यूह 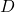 ज्ञात कीजिए कि
ज्ञात कीजिए कि 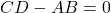 जहाँ
जहाँ 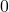 एक शून्य आव्यूह है।
एक शून्य आव्यूह है। - आव्यूह
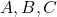 के लिए गुणन के साहचर्य नियम का सत्यापन कीजिए यदि
के लिए गुणन के साहचर्य नियम का सत्यापन कीजिए यदि 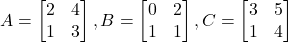 हो |
हो | - आव्यूह
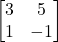 को एक सममित एवं एक विषम सममित आव्यूह के योग के रूप में व्यक्त कीजिए |
को एक सममित एवं एक विषम सममित आव्यूह के योग के रूप में व्यक्त कीजिए | - सिद्ध कीजिए कि वास्तविक अवयवों वाले किसी वर्ग आव्यूह
 के लिए
के लिए 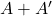 एक सममित एवं
एक सममित एवं  एक विषम सममित आव्यूह होते हैं |
एक विषम सममित आव्यूह होते हैं | - यदि
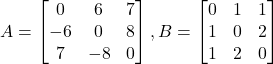 तथा
तथा 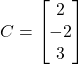 हो तो सत्यापित कीजिए कि
हो तो सत्यापित कीजिए कि 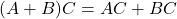
- यदि
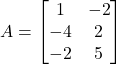 और
और 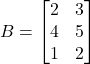 है दर्शाइए कि
है दर्शाइए कि  |
| - यदि
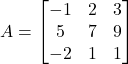 तथा
तथा  है तो सत्यापित कीजिए कि
है तो सत्यापित कीजिए कि 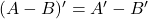
1 thought on “MP Board 12th mathematics Matrices Determinent Quarterly Exam 2025-26 Question Bank : 12वी गणित आव्यूह और सारणिक प्रश्न बैंक”