MP Board 12th Mathematics Inverse Trigonometric Functions Question Bank :
अध्याय-2 प्रतिलोम त्रिकोणमितीय फलन
स्मरणीय बिंदु
- प्रतिलोम त्रिकोणमितीय फलनों (मुख्य शाखा) के प्रांत तथा परिसर निम्न सारणी में वर्णित है :
| फलन | प्रांत | परिसर (मुख्य शाखा) |
|---|---|---|
| [-1,1] | |
| [-1,1] | |
| | |
| | |
| | |
| | |
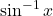 से
से 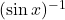 की भ्रान्ति नहीं होनी चाहिए। वास्तव में
की भ्रान्ति नहीं होनी चाहिए। वास्तव में 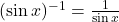 और इसी प्रकार ये तथ्य अन्य त्रिकोणमितीय फलनों के सत्य होता है।
और इसी प्रकार ये तथ्य अन्य त्रिकोणमितीय फलनों के सत्य होता है।- किसी प्रतिलोम त्रिकोणमितीय फलन का वह मान, जो उसकी मुख्य शाखा में स्थित होता है, प्रतिलोम त्रिकोणमितीय फलन का मुख्य मान (Principle Value) कहलाता है।
उपयुक्त प्रांतों के लिए :
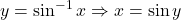 या
या 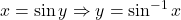
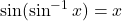 या
या 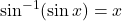
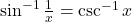
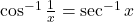
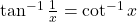
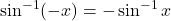
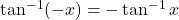
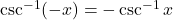
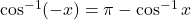
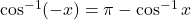
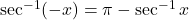
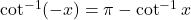
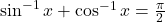
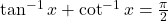
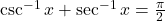
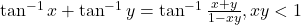
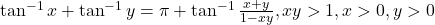
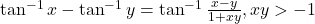
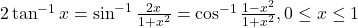
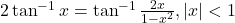
प्रश्न 1. सही विकल्प चुनिए –
(i) यदि ![]() तब
तब
(a) ![]()
(b) ![]()
(c) ![]()
(d) ![]()
(ii) ![]()
(a) ![]()
(b) ![]()
(c) ![]()
(d) ![]()
(iii) ![]()
(a) ![]()
(b) ![]()
(c) ![]()
(d) ![]()
(iv) ![]()
(a) ![]()
(b) ![]()
(c) ![]()
(d) ![]()
(v) ![]()
(a) ![]()
(b) ![]()
(c) ![]()
(d) ![]()
(vi) ![]()
(a) ![]()
(b) ![]()
(c) ![]()
(d) ![]()
(vii) ![]() , तब
, तब ![]()
(a) ![]()
(b) ![]()
(c) ![]()
(d) ![]()
(viii) ![]()
(a) ![]()
(b) ![]()
(c) ![]()
(d) ![]()
(ix) ![]() का मुख्य मान होता है-
का मुख्य मान होता है-
(अ) ![]()
(ब) ![]()
(स) ![]()
(द) ![]()
(x) ![]() का मुख्य मान होता है-
का मुख्य मान होता है-
(अ) ![]()
(ब) ![]()
(स) ![]()
(द) ![]()
(xi) ![]() का मुख्य मान –
का मुख्य मान –
(अ) ![]()
(ब) ![]()
(स) ![]()
(द) ![]()
(xii) ![]() बराबर है –
बराबर है –
(अ) ![]()
(ब) ![]()
(स) ![]()
(द) ![]()
(xiii) ![]() का मुख्य मान होता है
का मुख्य मान होता है
(अ) ![]()
(ब) ![]()
(स) ![]()
(द) ![]()
(xiv) ![]()
(अ) ![]()
(ब) ![]()
(स) ![]()
(द) ![]()
(xv) ![]()
(अ) ![]()
(ब) ![]()
(स) ![]()
(द) ![]()
(xvi) ![]() का मान होता है –
का मान होता है –
(अ) ![]()
(ब) ![]()
(स) ![]()
(द) ![]()
(xvii) ![]() का मान होता है
का मान होता है
(अ) ![]()
(ब) ![]()
(स) ![]()
(द) ![]()
(xviii) ![]() की मुख्य शाखा का परिसर होता है –
की मुख्य शाखा का परिसर होता है –
(अ) ![]()
(ब) ![]()
(स) ![]()
(द) ![]()
(xix) ![]() की मुख्य शाखा का परिसर होता है –
की मुख्य शाखा का परिसर होता है –
(अ) ![]()
(ब) ![]()
(स) ![]()
(द) ![]()
(xx) ![]() का प्रांत
का प्रांत
(अ) ![]()
(ब) ![]()
(स) ![]()
(द) ![]()
(xxi) ![]() का मान बराबर है –
का मान बराबर है –
(अ) ![]()
(ब) ![]()
(स) ![]()
(द) ![]()
(xxii) ![]() का मान बराबर है।
का मान बराबर है।
(अ) ![]()
(ब) ![]()
(स) ![]()
(द) ![]()
(xxiii) ![]() का मान
का मान
(अ) ![]()
(ब) ![]()
(स) ![]()
(द) ![]()
(xxiv) ![]() हो तो का मान बराबर है।
हो तो का मान बराबर है।
(अ) ![]()
(ब) ![]()
(स) ![]()
(द) ![]()
(xxv) ![]() का प्रांत –
का प्रांत –
(अ) ![]()
(ब) ![]()
(स) ![]()
(द) ![]()
प्रश्न 2. रिक्त स्थानो की पूर्ति कीजिए:
i. ![]() का प्रांत है।
का प्रांत है।
ii. ![]() की मुख्य मान शाखा है।
की मुख्य मान शाखा है।
प्रश्न 3. सत्य/असत्य लिखो
i. ![]() का प्रांत
का प्रांत ![]() है।
है।
ii. ![]() की मुख्य मान शाखा
की मुख्य मान शाखा ![]() है।
है।
प्रश्न 3. एक शब्द/वाक्य में उत्तर दीजिये :
i. ![]() का प्रांत लिखिये
का प्रांत लिखिये
ii. ![]() की मुख्य मान शाखा लिखिये।
की मुख्य मान शाखा लिखिये।
iii. ![]() का मान लिखिये।
का मान लिखिये।
iv. ![]() का मान लिखिये।
का मान लिखिये।
प्रश्न क्रमांक
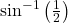 का मुख्य मान ज्ञात कीजिए।
का मुख्य मान ज्ञात कीजिए।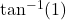 का मुख्य मान ज्ञात कीजिए।
का मुख्य मान ज्ञात कीजिए।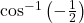 का मुख्य मान ज्ञात कीजिए।
का मुख्य मान ज्ञात कीजिए।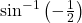 का मुख्य मान ज्ञात कीजिए।
का मुख्य मान ज्ञात कीजिए।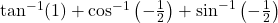 का मान ज्ञात कीजिए।
का मान ज्ञात कीजिए।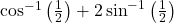 का मान ज्ञात कीजिए।
का मान ज्ञात कीजिए।- दर्शाइए कि
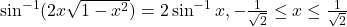
- दर्शाइए कि
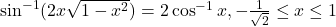
- सिद्ध कीजिये कि
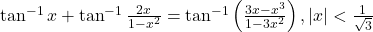
- सिद्ध कीजिये कि
![Rendered by QuickLaTeX.com 3\sin^{-1}x = \sin^{-1}(3x - 4x^3), x \in \left[-\frac{1}{2}, \frac{1}{2}\right]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-dcb37cdc60d9d8fa29aedd5614c5e260_l3.png)
- सिद्ध कीजिये कि
![Rendered by QuickLaTeX.com 3\cos^{-1}x = \cos^{-1}(4x^3 - 3x), x \in \left[\frac{1}{2}, 1\right]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-436a6ac9bbcdaffcacd6931812fe7835_l3.png)
- सिद्ध कीजिये कि
![Rendered by QuickLaTeX.com \tan^{-1}\sqrt{x} = \frac{1}{2}\cos^{-1}\left[\frac{1-x}{1+x}\right], x \in [0,1]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-4898a0aa95feec2708fe132fecd5289f_l3.png)
- सिद्ध कीजिये कि
![Rendered by QuickLaTeX.com \tan^{-1}\left[\frac{\sqrt{1+x}-\sqrt{1-x}}{\sqrt{1+x}+\sqrt{1-x}}\right] = \frac{\pi}{4} - \frac{1}{2}\cos^{-1}x, -\frac{1}{\sqrt{2}} \le x \le 1](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-1f0a927363c0d842d4ec4fba1accbdfa_l3.png) .
. ![Rendered by QuickLaTeX.com \cot^{-1}\left[\frac{1}{\sqrt{x^2-1}}\right], |x| > 1](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-381f09d6f609f4e14140d828c1cb821e_l3.png) को सरलतम रूप में लिखिये।
को सरलतम रूप में लिखिये।![Rendered by QuickLaTeX.com \tan^{-1}\left[\frac{x}{\sqrt{a^2-x^2}}\right], |x| > 1](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-477a7513929360572f0b096177869406_l3.png) को सरलतम रूप में लिखिये।
को सरलतम रूप में लिखिये।![Rendered by QuickLaTeX.com \tan^{-1}\left[\frac{\sqrt{1+x^2}-1}{x}\right], x \ne 0](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-48ed0f8e98d992df5ed1641f08d4ad45_l3.png) को सरलतम रूप में लिखिये।
को सरलतम रूप में लिखिये।![Rendered by QuickLaTeX.com \tan^{-1}\left[\sqrt{\frac{1-x}{1+x}}\right], |x| < 1](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-6a50e818fdc68b1576c4b459ec732e3e_l3.png) को सरलतम रूप में लिखिये।
को सरलतम रूप में लिखिये।![Rendered by QuickLaTeX.com \tan^{-1}\left[\frac{3a^2x-x^3}{a^3-3ax^2}\right], a>0, \frac{-a}{\sqrt{3}} \le x \le \frac{a}{\sqrt{3}}](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-1f0f3729a6b93fdbd36f5ab5f3a9b7ce_l3.png) को सरलतम रूप में लिखिये।
को सरलतम रूप में लिखिये।![Rendered by QuickLaTeX.com \tan^{-1}\left[\frac{\cos x}{1-\sin x}\right], -\frac{\pi}{2} < x < \frac{3\pi}{2}](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-2de812ddc666b9c486d8e8b6f19fa2e3_l3.png) को सरलतम रूप में लिखिये।
को सरलतम रूप में लिखिये।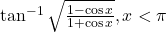 को सरलतम रूप में लिखिये।
को सरलतम रूप में लिखिये।![Rendered by QuickLaTeX.com \tan^{-1}\left[\frac{\cos x-\sin x}{\cos x+\sin x}\right], 0 < x < \pi](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-3ea359c47016175852f8f2aa554f5569_l3.png) को सरलतम रूप में लिखिये।
को सरलतम रूप में लिखिये।- सिद्ध कीजिये –
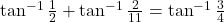
- सिद्ध कीजिये –
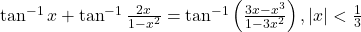
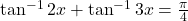 को सरल कीजिये।
को सरल कीजिये।- दर्शाइए कि
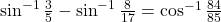
- सिद्ध कीजिये-
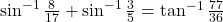
- सिद्ध कीजिये-
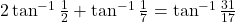
- फलन
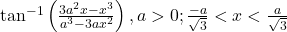 को सरलतम रूप में लिखिये।
को सरलतम रूप में लिखिये। - सरल कीजिये
![Rendered by QuickLaTeX.com \tan^{-1}\left[\frac{a\cos x-b\sin x}{b\cos x+a\sin x}\right]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-2ed4fa140519886f8ac2c4d9525815c2_l3.png) , if
, if 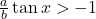
- सिद्ध कीजिये :
![Rendered by QuickLaTeX.com \tan^{-1}\left[\frac{\sqrt{1+\sin x}+\sqrt{1-\sin x}}{\sqrt{1+\sin x}-\sqrt{1-\sin x}}\right] = \frac{x}{2}, x \in \left[0, \frac{\pi}{4}\right]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-5e32781a2597c2c4dc7af617249f22cf_l3.png)
- दर्शाइए कि :
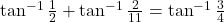
- सिद्ध कीजिये :
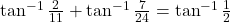
- हल कीजिये :
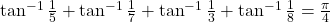
- सिद्ध कीजिये :
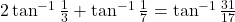
![Rendered by QuickLaTeX.com \tan\left[2\cos\left(2\sin^{-1}\frac{1}{2}\right)\right]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-24d35625d4c2b20d7d74ee7291b876bd_l3.png) का मान ज्ञात कीजिए।
का मान ज्ञात कीजिए।![Rendered by QuickLaTeX.com \tan\frac{1}{2}\left[\sin^{-1}\frac{2x}{1+x^2} + \cos^{-1}\frac{1-y^2}{1+y^2}\right], |x|<1, y>0](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-53e47fa9a235cf08e3968c5108165de9_l3.png) और
और 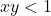 का मान ज्ञात कीजिए।
का मान ज्ञात कीजिए।- यदि
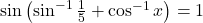 तो
तो  का मान ज्ञात कीजिए।
का मान ज्ञात कीजिए। - यदि
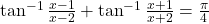 तो
तो  का मान ज्ञात कीजिए।
का मान ज्ञात कीजिए। - हल कीजिये
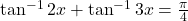
![Rendered by QuickLaTeX.com \sin^{-1}\left[\sin\frac{2\pi}{3}\right]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-447080fc123f092a9437791ed73ef2ff_l3.png) का मान ज्ञात कीजिए।
का मान ज्ञात कीजिए।![Rendered by QuickLaTeX.com \sin^{-1}\left[\sin\frac{3\pi}{5}\right]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-bb606e317c5794aecf3963324468e6f8_l3.png) का मान ज्ञात कीजिए।
का मान ज्ञात कीजिए।![Rendered by QuickLaTeX.com \tan^{-1}\left[\tan\frac{3\pi}{4}\right]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-4fe5b7ea98635147c37b8fcd65a58f91_l3.png) का मान ज्ञात कीजिए।
का मान ज्ञात कीजिए।![Rendered by QuickLaTeX.com \tan^{-1}\left[\tan\frac{7\pi}{6}\right]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-93b27e72bdf0f3c7ca78db05e72403f4_l3.png) का मान ज्ञात कीजिए।
का मान ज्ञात कीजिए।![Rendered by QuickLaTeX.com \cos^{-1}\left[\cos\frac{13\pi}{6}\right]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-a5b47e6be08fb78aaa19abd1a9f3210c_l3.png) का मान ज्ञात कीजिए।
का मान ज्ञात कीजिए।![Rendered by QuickLaTeX.com \tan\left[\sin^{-1}\frac{3}{5} + \cot^{-1}\frac{3}{2}\right]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-8a75a03c532e912c1b6334ee030c0e44_l3.png) का मान ज्ञात कीजिए।
का मान ज्ञात कीजिए।- दर्शाइए कि
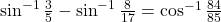
- दर्शाइए कि
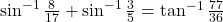
- दर्शाइए कि
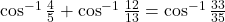
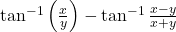 का मान ज्ञात कीजिए।
का मान ज्ञात कीजिए।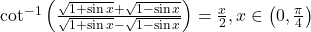
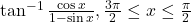 को सरलतम रूप में लिखिये।
को सरलतम रूप में लिखिये।![Rendered by QuickLaTeX.com \tan\frac{1}{2}\left[\sin^{-1}\frac{2x}{1+x^2} + \cos^{-1}\frac{1-y^2}{1+y^2}\right], |x|<1, y>0](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-53e47fa9a235cf08e3968c5108165de9_l3.png) तथा
तथा 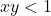 का मान ज्ञात कीजिए।
का मान ज्ञात कीजिए।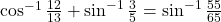 का मान ज्ञात कीजिए।
का मान ज्ञात कीजिए।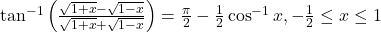 का मान ज्ञात कीजिए।
का मान ज्ञात कीजिए।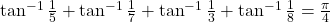 का मान ज्ञात कीजिए।
का मान ज्ञात कीजिए।
उत्तर- (अध्याय 2)
प्र.1. (i) b (ii) a (iii) b (iv) d (v) b (vi) d (vii) c (viii) c (ix) c (x) a (xi) b (xii) d (xiii) b (xiv) a (xv) b (xvi) a (xvii) c (xviii) a (xix) b (xx) a (xxi) b (xxii) b (xxiii) a (xxiv) c (xxv) b
प्र.2. (i) ![]() (ii)
(ii) ![]()
प्र.3. (i) सत्य (ii) सत्य
प्र.4. (i) ![]() (ii)
(ii) ![]() (iii) 0 (iv) 0
(iii) 0 (iv) 0