MP Board 12th Mathematics Integration Uses Question Bank: कक्षा 12 गणित अध्याय-8 समाकलन के अनुप्रयोग प्रश्न बैंक
अध्याय-8 समाकलन के अनुप्रयोग
स्मरणीय बिंदु
- वक्र
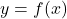 , x-अक्ष तथा भुजों
, x-अक्ष तथा भुजों  एवम्
एवम् 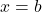 से घिरे भाग का क्षेत्रफल =
से घिरे भाग का क्षेत्रफल = 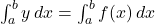
- वक्र
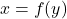 , y-अक्ष तथा कोटियों
, y-अक्ष तथा कोटियों 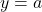 एवम्
एवम् 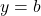 से घिरे भाग का क्षेत्रफल =
से घिरे भाग का क्षेत्रफल = 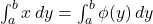
- दो वक्रो
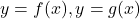 , तथा रेखाये
, तथा रेखाये  एवम्
एवम् 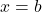 के मध्य घिरे भाग का क्षेत्रफल =
के मध्य घिरे भाग का क्षेत्रफल = ![Rendered by QuickLaTeX.com \int_a^b [f(x) - g(x)] \, dx](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-486386c4d4917da0599817c29f0fa6f2_l3.png)
- दो वक्रो
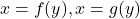 , तथा रेखाये
, तथा रेखाये 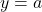 एवम्
एवम् 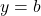 के मध्य घिरे भाग का क्षेत्रफल =
के मध्य घिरे भाग का क्षेत्रफल = ![Rendered by QuickLaTeX.com \int_a^b [f(y) - g(y)] \, dy](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-b8c3a2d4603ed89d9e149f008445b37e_l3.png)
- दीर्घवृत का समीकरण
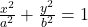 जहाँ x-अक्ष पर निर्देशांक
जहाँ x-अक्ष पर निर्देशांक 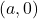 तथा y-अक्ष पर निर्देशांक
तथा y-अक्ष पर निर्देशांक 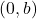 है।
है। - वृत का समीकरण
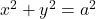 जहाँ x-अक्ष पर निर्देशांक
जहाँ x-अक्ष पर निर्देशांक 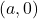 तथा y-अक्ष पर निर्देशांक
तथा y-अक्ष पर निर्देशांक 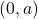 है।
है। - परवलय का समीकरण
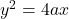 जहाँ शीर्ष
जहाँ शीर्ष 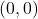 तथा नाभि निर्देशांक
तथा नाभि निर्देशांक 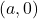 है।
है। - परवलय का समीकरण
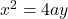 जहाँ शीर्ष
जहाँ शीर्ष 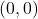 तथा नाभि निर्देशांक
तथा नाभि निर्देशांक 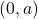 है।
है।
सही विकल्प चुनकर लिखिए :-
(i) प्रथम चतुर्थांश में वृत ![]() एवं रेखाओं
एवं रेखाओं ![]() से घिरे क्षेत्र का क्षेत्रफल है।
से घिरे क्षेत्र का क्षेत्रफल है।
(a) ![]()
(b) ![]()
(c) ![]()
(d) ![]()
(ii) वक्र ![]() , y-अक्ष एवं रेखा
, y-अक्ष एवं रेखा ![]() , से घिरे क्षेत्र का क्षेत्रफल है।
, से घिरे क्षेत्र का क्षेत्रफल है।
(a) 2
(b) ![]()
(c) ![]()
(d) ![]()
(iii) वक्र ![]() , x-अक्ष एवं कोटियों
, x-अक्ष एवं कोटियों ![]() तथा
तथा ![]() से घिरे क्षेत्र का क्षेत्रफल है।
से घिरे क्षेत्र का क्षेत्रफल है।
(a) -9
(b) ![]()
(c) ![]()
(d) ![]()
(iv) वक्र ![]() , x-अक्ष एवं कोटियों
, x-अक्ष एवं कोटियों ![]() तथा
तथा ![]() से घिरे क्षेत्र का क्षेत्रफल है।
से घिरे क्षेत्र का क्षेत्रफल है।
(a) 0
(b) ![]()
(c) ![]()
(d) ![]()
(v) दीर्घवृत ![]() का संपूर्ण क्षेत्रफल है –
का संपूर्ण क्षेत्रफल है –
(अ) ![]()
(ब) ![]()
(स) ![]()
(द) ![]()
(vi) वृत ![]() का क्षेत्रफल है –
का क्षेत्रफल है –
(अ) ![]()
(ब) ![]()
(स) ![]()
(द) ![]()
(vii) वक्र ![]() , रेखाओं
, रेखाओं ![]() एवम् x-अक्ष से घिरे क्षेत्र का क्षेत्रफल है –
एवम् x-अक्ष से घिरे क्षेत्र का क्षेत्रफल है –
(अ) ![]() वर्ग इकाई
वर्ग इकाई
(ब) ![]() वर्ग इकाई
वर्ग इकाई
(स) ![]() वर्ग इकाई
वर्ग इकाई
(द) ![]() वर्ग इकाई
वर्ग इकाई
(viii) ![]() के मध्य वक्र
के मध्य वक्र ![]() से घिरे क्षेत्र का क्षेत्रफल है –
से घिरे क्षेत्र का क्षेत्रफल है –
(अ) 4
(ब) 2
(स) 8
(द) 16
(ix) वक्र ![]() के धनात्मक x-अक्ष से घिरे क्षेत्र का क्षेत्रफल है –
के धनात्मक x-अक्ष से घिरे क्षेत्र का क्षेत्रफल है –
(अ) ![]()
(ब) ![]()
(स) 1
(द) ![]()
(x) y-अक्ष ![]() से घिरे क्षेत्र का क्षेत्रफल है –
से घिरे क्षेत्र का क्षेत्रफल है –
(अ) ![]()
(ब) ![]()
(स) ![]()
(द) 1
(xi) वक्र ![]() का x-अक्ष रेखाओं
का x-अक्ष रेखाओं ![]() से घिरे क्षेत्र का क्षेत्रफल है –
से घिरे क्षेत्र का क्षेत्रफल है –
(अ) 64 वर्ग इकाई
(ब) 32 वर्ग इकाई
(स) 16 वर्ग इकाई
(द) 128 वर्ग इकाई
(xii) ![]() एवम् रेखा
एवम् रेखा ![]() से घिरे भाग का क्षेत्रफल है –
से घिरे भाग का क्षेत्रफल है –
(अ) ![]() वर्ग इकाई
वर्ग इकाई
(ब) ![]() वर्ग इकाई
वर्ग इकाई
(स) ![]() वर्ग इकाई
वर्ग इकाई
(द) ![]() वर्ग इकाई
वर्ग इकाई
(xiii) वक्र ![]() , रेखाओं
, रेखाओं ![]() एवम् x-अक्ष से घिरे क्षेत्र का क्षेत्रफल है –
एवम् x-अक्ष से घिरे क्षेत्र का क्षेत्रफल है –
(अ) ![]() वर्ग इकाई
वर्ग इकाई
(ब) ![]() वर्ग इकाई
वर्ग इकाई
(स) ![]() वर्ग इकाई
वर्ग इकाई
(द) ![]() वर्ग इकाई
वर्ग इकाई
(xiv) वक्र ![]() , रेखा
, रेखा ![]() एवम् y-अक्ष से घिरे क्षेत्र का क्षेत्रफल है
एवम् y-अक्ष से घिरे क्षेत्र का क्षेत्रफल है
(अ) ![]() वर्ग इकाई
वर्ग इकाई
(ब) ![]() वर्ग इकाई
वर्ग इकाई
(स) ![]() वर्ग इकाई
वर्ग इकाई
(द) ![]() वर्ग इकाई
वर्ग इकाई
प्रश्न 2. रिक्त स्थान भरिये।
(i) वक्र ![]() का क्षेत्रफल ………………. है।
का क्षेत्रफल ………………. है।
(ii) वक्र ![]() का क्षेत्रफल ………………. है।
का क्षेत्रफल ………………. है।
(iii) वक्र ![]() रेखा
रेखा ![]() से घिरे क्षेत्र का क्षेत्रफल ………………. है।
से घिरे क्षेत्र का क्षेत्रफल ………………. है।
(iv) प्रथम चतुर्थांश में वृत ![]() से घिरे क्षेत्र का क्षेत्रफल ……… है।
से घिरे क्षेत्र का क्षेत्रफल ……… है।
(v) वक्र ![]() रेखा
रेखा ![]() एवम् y-अक्ष से घिरे क्षेत्र का क्षेत्रफल ……… है।
एवम् y-अक्ष से घिरे क्षेत्र का क्षेत्रफल ……… है।
(vi) दीर्घ वृत ![]() से घिरे क्षेत्र का क्षेत्रफल ……… है।
से घिरे क्षेत्र का क्षेत्रफल ……… है।
(vii) दीर्घ वृत ![]() से घिरे क्षेत्र का क्षेत्रफल ……… है।
से घिरे क्षेत्र का क्षेत्रफल ……… है।
(viii) वृत ![]() के एक चतुर्थांश का क्षेत्रफल ……… है।
के एक चतुर्थांश का क्षेत्रफल ……… है।
(ix) वक्र ![]() , x-अक्ष तथा रेखा
, x-अक्ष तथा रेखा ![]() व
व ![]() से घिरे क्षेत्र का क्षेत्रफल ….. है।
से घिरे क्षेत्र का क्षेत्रफल ….. है।
(x) वक्र ![]() , x-अक्ष तथा रेखा
, x-अक्ष तथा रेखा ![]() व
व ![]() से घिरे क्षेत्र का क्षेत्रफल ….. है।
से घिरे क्षेत्र का क्षेत्रफल ….. है।
प्रश्न 3. सही जोड़ी बनाइये।
| (i) | वृत | (अ) | |
|---|---|---|---|
| (ii) | वृत | (ब) | |
| (iii) | वक्र | (स) | |
| (iv) | वक्र | (द) | |
| (v) | रेखा | (इ) | |
| (vi) | वक्र | (फ) | 9 वर्ग इकाई |
प्रश्न क्रमांक
- वक्र
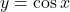 , x-अक्ष व
, x-अक्ष व 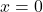 तथा
तथा 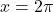 घिरे भाग का क्षेत्रफल ज्ञात कीजिये।
घिरे भाग का क्षेत्रफल ज्ञात कीजिये। - वक्र
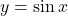 , x-अक्ष व
, x-अक्ष व 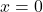 तथा
तथा 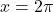 घिरे भाग का क्षेत्रफल ज्ञात कीजिये।
घिरे भाग का क्षेत्रफल ज्ञात कीजिये। - रेखा
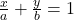 तथा निर्देशकों के क्षेत्र का क्षेत्रफल ज्ञात कीजिये।
तथा निर्देशकों के क्षेत्र का क्षेत्रफल ज्ञात कीजिये। - वक्र
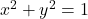 के प्रथम चतुर्थांश का क्षेत्रफल ज्ञात कीजिये।
के प्रथम चतुर्थांश का क्षेत्रफल ज्ञात कीजिये। - वृत
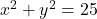 के क्षेत्रफल ज्ञात कीजिये।
के क्षेत्रफल ज्ञात कीजिये। - वक्र
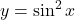 , x-अक्ष व
, x-अक्ष व 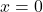 तथा
तथा  घिरे भाग का क्षेत्रफल ज्ञात कीजिये।
घिरे भाग का क्षेत्रफल ज्ञात कीजिये। - वक्र
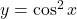 , x-अक्ष व
, x-अक्ष व 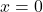 तथा
तथा  घिरे भाग का क्षेत्रफल ज्ञात कीजिये।
घिरे भाग का क्षेत्रफल ज्ञात कीजिये। - वक्र
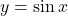 , x-अक्ष व
, x-अक्ष व 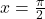 तथा
तथा 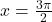 घिरे भाग का क्षेत्रफल ज्ञात कीजिये।
घिरे भाग का क्षेत्रफल ज्ञात कीजिये। - वक्र
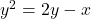 , y-अक्ष घिरे भाग का क्षेत्रफल ज्ञात कीजिये।
, y-अक्ष घिरे भाग का क्षेत्रफल ज्ञात कीजिये। - रेखा
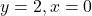 तथा
तथा 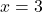 घिरे भाग का क्षेत्रफल ज्ञात कीजिये।
घिरे भाग का क्षेत्रफल ज्ञात कीजिये। - वक्र
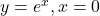 तथा
तथा 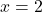 घिरे भाग का क्षेत्रफल ज्ञात कीजिये।
घिरे भाग का क्षेत्रफल ज्ञात कीजिये। - वक्र
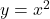 रेखा
रेखा 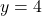 घिरे भाग का क्षेत्रफल ज्ञात कीजिये।
घिरे भाग का क्षेत्रफल ज्ञात कीजिये। - परवलय
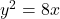 तथा सरल रेखा
तथा सरल रेखा 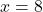 के बीच का क्षेत्रफल ज्ञात कीजिये।
के बीच का क्षेत्रफल ज्ञात कीजिये। - परवलय
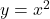 तथा सरल रेखा
तथा सरल रेखा 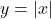 से घिरे भाग का क्षेत्रफल ज्ञात कीजिये।
से घिरे भाग का क्षेत्रफल ज्ञात कीजिये। - परवलय
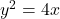 तथा सरल रेखा
तथा सरल रेखा 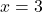 से घिरे भाग का क्षेत्रफल ज्ञात कीजिये।
से घिरे भाग का क्षेत्रफल ज्ञात कीजिये। - वक्र
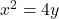 व सरल रेखा
व सरल रेखा 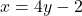 के बीच के क्षेत्रफल ज्ञात कीजिये।
के बीच के क्षेत्रफल ज्ञात कीजिये। - परवलय
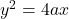 तथा उसकी नाभिलम्ब जीवा से घिरे भाग का क्षेत्रफल ज्ञात कीजिये।
तथा उसकी नाभिलम्ब जीवा से घिरे भाग का क्षेत्रफल ज्ञात कीजिये। - दीर्घवृत
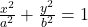 एवं कोटिओं
एवं कोटिओं 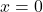 और
और 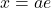 से घिरे भाग का क्षेत्रफल ज्ञात कीजिये। जहाँ
से घिरे भाग का क्षेत्रफल ज्ञात कीजिये। जहाँ 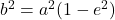 एवं
एवं 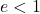 है।
है। - वृत
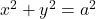 का संपूर्ण क्षेत्रफल ज्ञात कीजिये।
का संपूर्ण क्षेत्रफल ज्ञात कीजिये। - परवलय
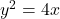 तथा सरल रेखा
तथा सरल रेखा 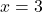 से घिरे भाग का क्षेत्रफल ज्ञात कीजिये।
से घिरे भाग का क्षेत्रफल ज्ञात कीजिये। 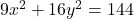 व सरल रेखा
व सरल रेखा 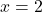 से खंडित लघु भाग का क्षेत्रफल ज्ञात कीजिये।
से खंडित लघु भाग का क्षेत्रफल ज्ञात कीजिये।- वक्र
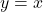 का x-अक्ष तथा रेखाओं
का x-अक्ष तथा रेखाओं 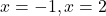 के घिरे भाग का क्षेत्रफल ज्ञात कीजिये।
के घिरे भाग का क्षेत्रफल ज्ञात कीजिये। - वक्र
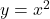 तथा रेखा
तथा रेखा 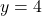 घिरे भाग का क्षेत्रफल ज्ञात कीजिये।
घिरे भाग का क्षेत्रफल ज्ञात कीजिये। - दीर्घवृत
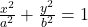 तथा रेखा
तथा रेखा 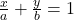 से घिरे भाग का क्षेत्रफल ज्ञात कीजिये।
से घिरे भाग का क्षेत्रफल ज्ञात कीजिये। - समाकलन का उपयोग करते हुये त्रिभुज का क्षेत्रफल ज्ञात कीजिये जिसके शीर्ष
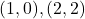 व
व 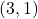 है।
है। - परवलय
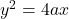 तथा रेखा
तथा रेखा 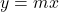 से घिरे भाग का क्षेत्रफल ज्ञात कीजिये।
से घिरे भाग का क्षेत्रफल ज्ञात कीजिये। - उस त्रिभुज का क्षेत्रफल समाकलन द्वारा ज्ञात कीजिये जिसके भुजाये
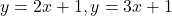 व
व 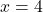 है।
है। - परवलय
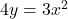 से रेखा
से रेखा 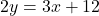 द्वारा कटे भाग का क्षेत्रफल ज्ञात कीजिये।
द्वारा कटे भाग का क्षेत्रफल ज्ञात कीजिये। - वृत
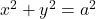 तथा रेखा
तथा रेखा 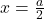 से घिरे छोटे भाग का क्षेत्रफल ज्ञात कीजिये।
से घिरे छोटे भाग का क्षेत्रफल ज्ञात कीजिये। - समाकलन का उपयोग करते हुये त्रिभुज का क्षेत्रफल ज्ञात कीजिये जिसके शीर्ष
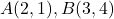 व
व 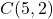 है।
है। - समाकलन विधि से रेखाओं
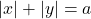 घिरे भाग का क्षेत्रफल ज्ञात कीजिये।
घिरे भाग का क्षेत्रफल ज्ञात कीजिये। - वक्र
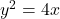 , एवं रेखा
, एवं रेखा 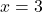 से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए। - प्रथम चतुर्थांश में वृत
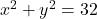 , रेखा
, रेखा 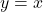 एवं x-अक्ष से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
एवं x-अक्ष से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए। - दीर्घवृत
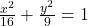 से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए। - वक्र
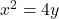 , एवं रेखा
, एवं रेखा 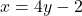 से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए। - छेदक रेखा
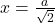 द्वारा वृत
द्वारा वृत 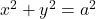 के छोटे भाग का क्षेत्रफल ज्ञात कीजिए।
के छोटे भाग का क्षेत्रफल ज्ञात कीजिए।
प्रश्न क्रमांक-4 निम्नलिखित में से सत्य/असत्य लिखिए।
(i) वक्र ![]() अक्ष एवं रेखाओं
अक्ष एवं रेखाओं ![]() तथा
तथा ![]() से घिरे क्षेत्र का क्षेत्रफल
से घिरे क्षेत्र का क्षेत्रफल ![]() है।
है।
(ii) किसी वृत ![]() का क्षेत्रफल
का क्षेत्रफल ![]() होता है।
होता है।
(iii) वक्र ![]() का क्षेत्रफल
का क्षेत्रफल ![]() वर्ग इकाई है।
वर्ग इकाई है।
(iv) दीर्घ वृत ![]() से घिरे क्षेत्र का क्षेत्रफल
से घिरे क्षेत्र का क्षेत्रफल ![]() वर्ग इकाई है।
वर्ग इकाई है।
(v) वक्र ![]() व y-अक्ष से घिरे क्षेत्र का क्षेत्रफल 16 वर्ग इकाई है।
व y-अक्ष से घिरे क्षेत्र का क्षेत्रफल 16 वर्ग इकाई है।
(vi) वृत ![]() का क्षेत्रफल
का क्षेत्रफल ![]() वर्ग इकाई है।
वर्ग इकाई है।
(vii) वृत ![]() के एक चतुर्थांश का क्षेत्रफल
के एक चतुर्थांश का क्षेत्रफल ![]() वर्ग इकाई है।
वर्ग इकाई है।
(viii) वक्र ![]() का क्षेत्रफल
का क्षेत्रफल ![]() वर्ग इकाई है।
वर्ग इकाई है।
(ix) ![]() का समाकलन
का समाकलन ![]()
(x) ![]() का मान
का मान ![]() होता है।
होता है।
(xi) ![]() होता है।
होता है।
(xii) ![]() होता है।
होता है।
प्रश्न क्रमांक- 5 एक शब्द/वाक्य में उत्तर दीजिए।
(i) वक्र ![]() , रेखाओं
, रेखाओं ![]() एवं x-अक्ष से घिरे क्षेत्र का प्रथम चतुर्थांश में क्षेत्रफल क्या होगा ?
एवं x-अक्ष से घिरे क्षेत्र का प्रथम चतुर्थांश में क्षेत्रफल क्या होगा ?
(ii) वक्र ![]() एवं y-अक्ष से घिरे क्षेत्र का क्षेत्रफल क्या है ?
एवं y-अक्ष से घिरे क्षेत्र का क्षेत्रफल क्या है ?
(iii) प्रथम चतुर्थांश में वृत ![]() एवम् रेखाओं
एवम् रेखाओं ![]() से घिरे क्षेत्र का क्षेत्रफल क्या होगा ?
से घिरे क्षेत्र का क्षेत्रफल क्या होगा ?
(iv) वृत ![]() का क्षेत्रफल क्या होगा ?
का क्षेत्रफल क्या होगा ?
(v) वक्र ![]() व
व ![]() व x-अक्ष से घिरे क्षेत्र का क्षेत्रफल क्या होगा ?
व x-अक्ष से घिरे क्षेत्र का क्षेत्रफल क्या होगा ?
(vi) वक्र ![]() व x-अक्ष से घिरे क्षेत्र का क्षेत्रफल क्या होगा ?
व x-अक्ष से घिरे क्षेत्र का क्षेत्रफल क्या होगा ?
(vii) वक्र ![]() व
व ![]() से घिरे क्षेत्र का क्षेत्रफल क्या होगा ?
से घिरे क्षेत्र का क्षेत्रफल क्या होगा ?
(viii) वक्र ![]() व x-अक्ष से घिरे क्षेत्र का क्षेत्रफल क्या होगा ?
व x-अक्ष से घिरे क्षेत्र का क्षेत्रफल क्या होगा ?
(ix) वक्र ![]() व
व ![]() व x-अक्ष से घिरे क्षेत्र का क्षेत्रफल क्या होगा ?
व x-अक्ष से घिरे क्षेत्र का क्षेत्रफल क्या होगा ?
(x) वक्र ![]() व x-अक्ष से घिरे क्षेत्र का क्षेत्रफल क्या होगा ?
व x-अक्ष से घिरे क्षेत्र का क्षेत्रफल क्या होगा ?
(xi) वक्र ![]() व सरल रेखा
व सरल रेखा ![]() घिरे क्षेत्र का क्षेत्रफल क्या होगा ?
घिरे क्षेत्र का क्षेत्रफल क्या होगा ?
(xii) वृत ![]() द्वारा परिबद्ध क्षेत्र का क्षेत्रफल क्या होगा
द्वारा परिबद्ध क्षेत्र का क्षेत्रफल क्या होगा
(उत्तर) अध्याय-8
प्रश्न 1. i) a ii) b iii) d iv) c v) ![]() vi)
vi) ![]() vii)
vii) ![]() viii)
viii) ![]() वर्ग इकाई (ix) 4 (x)
वर्ग इकाई (ix) 4 (x) ![]() (xi)
(xi) ![]() (xii) 64 वर्ग इकाई (xiii)
(xii) 64 वर्ग इकाई (xiii) ![]() वर्ग इकाई (xiv)
वर्ग इकाई (xiv) ![]() वर्ग इकाई (xv)
वर्ग इकाई (xv) ![]() वर्ग इकाई
वर्ग इकाई
प्रश्न 2. (i) ![]() वर्ग इकाई (ii)
वर्ग इकाई (ii) ![]() वर्ग इकाई (iii)
वर्ग इकाई (iii) ![]() वर्ग इकाई (iv)
वर्ग इकाई (iv) ![]() वर्ग इकाई (v)
वर्ग इकाई (v) ![]() वर्ग इकाई (vi)
वर्ग इकाई (vi) ![]() वर्ग इकाई (vii)
वर्ग इकाई (vii) ![]() वर्ग इकाई (viii)
वर्ग इकाई (viii) ![]() वर्ग इकाई (ix)
वर्ग इकाई (ix) ![]() वर्ग इकाई (x)
वर्ग इकाई (x) ![]()
प्रश्न 3. (i) ![]() वर्ग इकाई (ii)
वर्ग इकाई (ii) ![]() वर्ग इकाई (iii)
वर्ग इकाई (iii) ![]() वर्ग इकाई (iv)
वर्ग इकाई (iv) ![]() वर्ग इकाई (v) 9 वर्ग इकाई (vi)
वर्ग इकाई (v) 9 वर्ग इकाई (vi) ![]() वर्ग इकाई
वर्ग इकाई
प्रश्न 4. i) सत्य ii) असत्य iii) असत्य iv) सत्य v) असत्य vi) असत्य vii) सत्य viii) सत्य ix) सत्य x) असत्य (xi) सत्य (xii) सत्य
प्रश्न 5. (i) ![]() वर्ग इकाई (ii)
वर्ग इकाई (ii) ![]() वर्ग इकाई (iii)
वर्ग इकाई (iii) ![]() वर्ग इकाई (iv)
वर्ग इकाई (iv) ![]() वर्ग इकाई (v)
वर्ग इकाई (v) ![]() वर्ग इकाई (vi)
वर्ग इकाई (vi) ![]() वर्ग इकाई (vii) 9 वर्ग इकाई (viii)
वर्ग इकाई (vii) 9 वर्ग इकाई (viii) ![]() वर्ग इकाई (ix)
वर्ग इकाई (ix) ![]() वर्ग इकाई (x)
वर्ग इकाई (x) ![]() वर्ग इकाई (xi) 18 वर्ग इकाई (xii)
वर्ग इकाई (xi) 18 वर्ग इकाई (xii) ![]() वर्ग इकाई
वर्ग इकाई