MP Board 12th Mathematics Differentiability Uses Question Bank : कक्षा 12 गणित अध्याय-6 अवकलज के अनुप्रयोग प्रश्न बैंक
अध्याय-6 अवकलज के अनुप्रयोग
स्मरणीय बिंदु –
- यदि एक राशि
 एक दूसरी राशि
एक दूसरी राशि  के सापेक्ष किसी नियम
के सापेक्ष किसी नियम 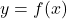 को संतुष्ट करते हुए परिवर्तित होती है तो
को संतुष्ट करते हुए परिवर्तित होती है तो 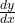 (या
(या 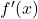 )
)  के सापेक्ष
के सापेक्ष  के परिवर्तन की दर को निरूपित करता है। और
के परिवर्तन की दर को निरूपित करता है। और ![Rendered by QuickLaTeX.com \left.\frac{dy}{dx}\right]_{x=x_0}](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-a061b51509617464a2af5f2bfbfa2d49_l3.png) (या
(या 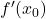 )
) 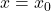 पर
पर  के सापेक्ष
के सापेक्ष  के परिवर्तन की दर को निरूपित करता है।
के परिवर्तन की दर को निरूपित करता है। - यदि दो राशियाँ
 और
और 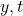 के सापेक्ष परिवर्तित हो रहीं हों अर्थात्
के सापेक्ष परिवर्तित हो रहीं हों अर्थात् 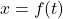 और
और 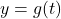 , तब श्रृंखला नियम से
, तब श्रृंखला नियम से 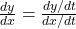 , यदि
, यदि 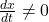
- एक फलन
 अंतराल
अंतराल
(a)![Rendered by QuickLaTeX.com [a,b]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-b4670559c4f8d351511ca9a22b8506b9_l3.png) में वर्धमान है यदि
में वर्धमान है यदि ![Rendered by QuickLaTeX.com [a,b]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-b4670559c4f8d351511ca9a22b8506b9_l3.png) में
में 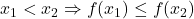 , सभी
, सभी 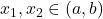 के लिए। [cite_start]विकल्पतः यदि प्रत्येक
के लिए। [cite_start]विकल्पतः यदि प्रत्येक ![Rendered by QuickLaTeX.com x \in [a,b]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-9650d0802ece688931fa8910b09a67c7_l3.png) के लिए
के लिए 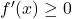 , है। [cite: 5]
, है। [cite: 5]
(b) अंतराल![Rendered by QuickLaTeX.com [a,b]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-b4670559c4f8d351511ca9a22b8506b9_l3.png) में ह्रासमान है यदि
में ह्रासमान है यदि ![Rendered by QuickLaTeX.com [a,b]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-b4670559c4f8d351511ca9a22b8506b9_l3.png) में
में 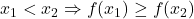 , सभी
, सभी 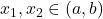 के लिए। [cite_start]विकल्पतः यदि प्रत्येक
के लिए। [cite_start]विकल्पतः यदि प्रत्येक ![Rendered by QuickLaTeX.com x \in [a,b]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-9650d0802ece688931fa8910b09a67c7_l3.png) के लिए
के लिए 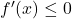 , है। [cite: 5]
, है। [cite: 5] - [cite_start]फलन
 के प्रांत में एक बिंदु
के प्रांत में एक बिंदु  जिस पर या तो
जिस पर या तो 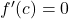 या
या  अवकलनीय नहीं है,
अवकलनीय नहीं है,  का क्रांतिक बिंदु कहलाता है। [cite: 5]
का क्रांतिक बिंदु कहलाता है। [cite: 5]
प्रथम अवकलज परीक्षण
मान लीजिए एक विवृत अंतराल ![]() पर फलन
पर फलन ![]() परिभाषित है। [cite_start]मान लीजिए
परिभाषित है। [cite_start]मान लीजिए ![]() में एक क्रांतिक बिंदु
में एक क्रांतिक बिंदु ![]() पर फलन
पर फलन ![]() संतत है तब: [cite: 3]
संतत है तब: [cite: 3]
- [cite_start](a) जब
 बिंदु
बिंदु  के बायीं ओर से दायीं ओर बढ़ता है तब
के बायीं ओर से दायीं ओर बढ़ता है तब 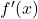 का चिन्ह धन से ऋण में परिवर्तित होता है अर्थात्
का चिन्ह धन से ऋण में परिवर्तित होता है अर्थात्  के बायीं ओर और पर्याप्त निकट प्रत्येक बिंदु पर यदि
के बायीं ओर और पर्याप्त निकट प्रत्येक बिंदु पर यदि 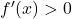 तथा
तथा  के दायीं ओर और पर्याप्त निकट प्रत्येक बिंदु पर यदि
के दायीं ओर और पर्याप्त निकट प्रत्येक बिंदु पर यदि 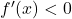 तब
तब  स्थानीय उच्चतम का एक बिंदु है। [cite: 3]
स्थानीय उच्चतम का एक बिंदु है। [cite: 3] - [cite_start](b) जब
 बिंदु
बिंदु  के बायीं ओर से दायीं ओर बढ़ता है तब
के बायीं ओर से दायीं ओर बढ़ता है तब 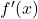 का चिन्ह ऋण से धन में परिवर्तित होता है अर्थात्
का चिन्ह ऋण से धन में परिवर्तित होता है अर्थात्  के बायीं ओर और पर्याप्त निकट प्रत्येक बिंदु पर यदि
के बायीं ओर और पर्याप्त निकट प्रत्येक बिंदु पर यदि 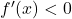 तथा
तथा  के दायीं ओर और पर्याप्त निकट प्रत्येक बिंदु पर यदि
के दायीं ओर और पर्याप्त निकट प्रत्येक बिंदु पर यदि 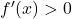 तब
तब  स्थानीय निम्नतम का एक बिंदु है। [cite: 2]
स्थानीय निम्नतम का एक बिंदु है। [cite: 2] - [cite_start](c) जब
 बिंदु
बिंदु  के बायीं ओर से दायीं ओर बढ़ता है तब
के बायीं ओर से दायीं ओर बढ़ता है तब 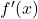 परिवर्तित नहीं होता है तब
परिवर्तित नहीं होता है तब  न तो स्थानीय उच्चतम का एक बिंदु है और न ही स्थानीय निम्नतम का एक बिंदु है तब ब नति परिवर्तन का बिंदु है। [cite: 2]
न तो स्थानीय उच्चतम का एक बिंदु है और न ही स्थानीय निम्नतम का एक बिंदु है तब ब नति परिवर्तन का बिंदु है। [cite: 2]
द्वितीय अवकलज परीक्षण
[cite_start]मान लीजिए एक अंतराल ![]() पर
पर ![]() एक परिभाषित फलन है और
एक परिभाषित फलन है और ![]() है, मान लीजिए
है, मान लीजिए ![]() पर लगातार दो बार अवकलनीय है, तब: [cite: 1]
पर लगातार दो बार अवकलनीय है, तब: [cite: 1]
- (i) यदि
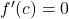 और
और 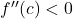 तब
तब  स्थानीय उच्चतम का एक बिंदु है। [cite_start]
स्थानीय उच्चतम का एक बिंदु है। [cite_start] का स्थानीय उच्चतम मान
का स्थानीय उच्चतम मान 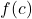 है। [cite: 1]
है। [cite: 1] - (ii) यदि
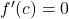 और
और 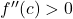 तब
तब  स्थानीय निम्नतम का एक बिंदु है। [cite_start]
स्थानीय निम्नतम का एक बिंदु है। [cite_start] का स्थानीय निम्नतम मान
का स्थानीय निम्नतम मान 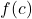 है। [cite: 1]
है। [cite: 1] - (iii) यदि
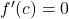 और
और 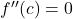 तब यह परीक्षण असफल रहता है। [cite_start]इस स्थिति में हम पुनः वापस प्रथम अवकलज परीक्षण का प्रयोग करते हैं और यह ज्ञात करते हैं कि
तब यह परीक्षण असफल रहता है। [cite_start]इस स्थिति में हम पुनः वापस प्रथम अवकलज परीक्षण का प्रयोग करते हैं और यह ज्ञात करते हैं कि  उच्चतम, निम्नतम या नति परिवर्तन का बिंदु है। [cite: 1]
उच्चतम, निम्नतम या नति परिवर्तन का बिंदु है। [cite: 1]
निरपेक्ष उच्चतम और निरपेक्ष निम्नतम मानों को ज्ञात करने की व्यावहारिक विधि है:
[cite_start]चरण 1: अंतराल में ![]() के सभी क्रांतिक बिंदु ज्ञात कीजिए अर्थात्
के सभी क्रांतिक बिंदु ज्ञात कीजिए अर्थात् ![]() के वे सभी मान ज्ञात कीजिए जहाँ या तो
के वे सभी मान ज्ञात कीजिए जहाँ या तो ![]() या
या ![]() अवकलनीय नहीं है। [cite: 1]
अवकलनीय नहीं है। [cite: 1]
[cite_start]चरण 2: अंतराल के अंत्य बिंदु लीजिए। [cite: 4]
[cite_start]चरण 3: (चरण 1 व 2 से प्राप्त) सभी बिंदुओं पर ![]() के मानों की गणना कीजिए। [cite: 4]
के मानों की गणना कीजिए। [cite: 4]
चरण 4: चरण 3 में गणना से प्राप्त ![]() के सभी मानों में से उच्चतम और निम्नतम मानों को लीजिए। [cite_start]यही उच्चतम मान
के सभी मानों में से उच्चतम और निम्नतम मानों को लीजिए। [cite_start]यही उच्चतम मान ![]() का निरपेक्ष उच्चतम मान और निम्नतम मान
का निरपेक्ष उच्चतम मान और निम्नतम मान ![]() का निरपेक्ष निम्नतम मान होंगे। [cite: 4]
का निरपेक्ष निम्नतम मान होंगे। [cite: 4]
प्रश्न क्रमांक 1- सही विकल्प चुनकर लिखिए।
(i) एक वृत की त्रिज्या ![]() पर
पर ![]() के सापेक्ष क्षेत्रफल में परिवर्तन की दर है :
के सापेक्ष क्षेत्रफल में परिवर्तन की दर है :
(a) ![]() (b)
(b) ![]() (c)
(c) ![]() (d)
(d) ![]()
(ii) एक उत्पाद की ![]() इकाइयों के विक्रय से प्राप्त कुल आय रूपयों में
इकाइयों के विक्रय से प्राप्त कुल आय रूपयों में ![]() से प्रदत्त है, जब
से प्रदत्त है, जब ![]() है तो सीमांत आय है :
है तो सीमांत आय है :
(a) 116 (b) 96 (c) 90 (d) 126
(iii) निम्नलिखित में कौन से फलन ![]() में निरंतर ह्रासमान नही है :
में निरंतर ह्रासमान नही है :
(a) ![]() (b)
(b) ![]() (c)
(c) ![]() (d) इनमें से कोई नहीं
(d) इनमें से कोई नहीं
(iv) निम्नलिखित अंतरालों में से किस अंतराल में ![]() द्वारा प्रदत्त फलन
द्वारा प्रदत्त फलन ![]() निरंतर ह्रासमान है :
निरंतर ह्रासमान है :
(a) ![]() (b)
(b) ![]() (c)
(c) ![]() (d) इनमें से कोई नहीं
(d) इनमें से कोई नहीं
(v) निम्नलिखित में से किस अंतराल में ![]() वर्धमान है ?
वर्धमान है ?
(a) ![]() (b)
(b) ![]() (c)
(c) ![]() (d)
(d) ![]()
(vi) ![]() के सभी वास्तविक मानों के लिए
के सभी वास्तविक मानों के लिए ![]() का न्यूनतम मान है :
का न्यूनतम मान है :
(a) 0 (b) 1 (c) 3 (d) ![]()
(vii) ![]() का उच्चतम मान है:
का उच्चतम मान है:
(a) ![]() (b)
(b) ![]() (c) 1 (d) 0
(c) 1 (d) 0
(viii) एक ![]() त्रिज्या के बेलनाकार टंकी में
त्रिज्या के बेलनाकार टंकी में ![]() की दर से गेहूँ भरा जाता है। भरे गए गेहूँ की गहराई की वृद्धि दर है:
की दर से गेहूँ भरा जाता है। भरे गए गेहूँ की गहराई की वृद्धि दर है:
(a) ![]() (b)
(b) ![]() (c)
(c) ![]() (d)
(d) ![]()
प्रश्न क्रमांक 2-एक शब्द/वाक्य में उत्तर दीजिए
(i) ![]() का उच्चतम मान क्या है ?
का उच्चतम मान क्या है ?
(ii) वक्र ![]() और
और ![]() एक दूसरे को समकोण पर काटते है यदि
एक दूसरे को समकोण पर काटते है यदि ![]() ?
?
(iii) ![]() के सभी वास्तविक मानों के लिए
के सभी वास्तविक मानों के लिए ![]() का न्यूनतम मान क्या है ?
का न्यूनतम मान क्या है ?
(iv) किस अंतराल में ![]() से प्रदत्त फलन न तो वर्धमान है और न ही ह्रासमान है।
से प्रदत्त फलन न तो वर्धमान है और न ही ह्रासमान है।
(v) यदि ![]() और
और ![]() , तब श्रृंखला नियम से
, तब श्रृंखला नियम से ![]() बराबर क्या होगा ?
बराबर क्या होगा ?
प्रश्न क्रमांक 3-रिक्त स्थानों की पूर्ति कीजिए
(i) एक ![]() त्रिज्या के बेलनाकार टंकी में
त्रिज्या के बेलनाकार टंकी में ![]() की दर से गेहूँ भरा जाता है, भरे गए गेहूँ की गहराई की वृद्धि दर ………. है।
की दर से गेहूँ भरा जाता है, भरे गए गेहूँ की गहराई की वृद्धि दर ………. है।
(ii) ![]() से प्रदत फलन अंतराल
से प्रदत फलन अंतराल ![]() में ………. है
में ………. है
(iii) एक दिए हुए वृत में खींचे गए सभी आयतों में वर्ग का क्षेत्रफल ………. होता है।
(iv) ![]() से प्रदत फलन अंतराल ………. में निरंतर ह्रासमान है
से प्रदत फलन अंतराल ………. में निरंतर ह्रासमान है
(v) वक्र ![]() और
और ![]() एक दूसरे को ………. पर काटते है यदि
एक दूसरे को ………. पर काटते है यदि ![]()
(vi) एक शंकु के अंतर्गत महत्तम वक्रपृष्ठ वाले लंब वृत्तीय बेलन की त्रिज्या शंकु की त्रिज्या की ………. होती है।
(vii) यदि ![]() और
और ![]() तब
तब ![]() , ………. का एक बिंदु है। (viii) यदि
, ………. का एक बिंदु है। (viii) यदि ![]() और
और ![]() तब
तब ![]() , ………. का एक बिंदु है।
, ………. का एक बिंदु है।
प्रश्न क्रमांक 4-निम्न लिखित मे से सत्य/असत्य लिखिए:
(i) किसी उत्पाद की ![]() इकाईयों के विक्रय से प्राप्त कुल आय रूपए में
इकाईयों के विक्रय से प्राप्त कुल आय रूपए में ![]() से प्रदत्त है, जब
से प्रदत्त है, जब ![]() है तो सीमांत आय 36 रू. होगी।
है तो सीमांत आय 36 रू. होगी।
(ii) वृत के क्षेत्रफल के परिवर्तन की दर इसकी त्रिज्या ![]() के सापेक्ष
के सापेक्ष ![]() होगी जबकि
होगी जबकि ![]()
(iii) न्यूनतम पृष्ठ का दिए आयतन के लंब वृत्तीय शंकु की ऊँचाई आधार की त्रिज्या की 2 गुनी होती है।
(iv) दी हुई तिर्यक ऊँचाई और महत्तम आयतन वाले शंकु अर्द्ध शीर्ष कोण ![]() होता है |
होता है |
(v) यदि ![]() और
और ![]() तब
तब ![]() स्थानीय निम्नतम का एक बिंदु है।
स्थानीय निम्नतम का एक बिंदु है। ![]() का स्थानीय निम्नतम मान
का स्थानीय निम्नतम मान ![]() है।
है।
(vi) यदि ![]() और
और ![]() तब
तब ![]() स्थानीय उच्चतम का एक बिंदु है।
स्थानीय उच्चतम का एक बिंदु है। ![]() का स्थानीय उच्चतम मान
का स्थानीय उच्चतम मान ![]() है।
है।
प्रश्न क्रमांक
- दर्शाइए कि वक्र
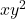 और
और 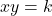 एक दूसरे को समकोण पर काटते है यदि
एक दूसरे को समकोण पर काटते है यदि 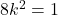
- एक 5 मीटर लंबी सीढ़ी दीवार से टिकी है। सीढ़ी के निचले सिरे को दीवार से
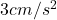 की दर से हटाया जाता है सीढ़ी की दीवार पर ऊँचाई किस दर से कम होगी जब इसका निचला सिरा दीवार से 4 मी. दूर हो।
की दर से हटाया जाता है सीढ़ी की दीवार पर ऊँचाई किस दर से कम होगी जब इसका निचला सिरा दीवार से 4 मी. दूर हो। - सिद्ध कीजिए कि एक दिए हुए वृत में खींचे गए सभी आयतों में वर्ग का क्षेत्रफल उच्चिष्ठ होता है।
- दो धनात्मक संख्याएँ
 और
और  ज्ञात कीजिए जिनका योग 35 और गुणनफल महत्तम हो।
ज्ञात कीजिए जिनका योग 35 और गुणनफल महत्तम हो। - फलन
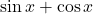 का महत्तम मान ज्ञात करो।
का महत्तम मान ज्ञात करो। - यदि अंतराल
![Rendered by QuickLaTeX.com [0,2]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-1571666a47302be9ed925a760be14ff0_l3.png) में
में 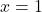 पर फलन
पर फलन  उच्चतम मान प्राप्त करता है तो
उच्चतम मान प्राप्त करता है तो  का मान ज्ञात कीजिए।
का मान ज्ञात कीजिए। - सिद्ध कीजिए
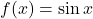 से प्रदत्त फलन
से प्रदत्त फलन
(i)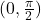 में निरंतर वर्धमान है
में निरंतर वर्धमान है
(ii)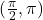 में निरंतर ह्रासमान है
में निरंतर ह्रासमान है
(iii)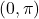 में न तो वर्धमान है और न ही ह्रासमान है
में न तो वर्धमान है और न ही ह्रासमान है - अंतराल ज्ञात कीजिए जिनमें
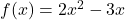 से प्रदत्त फलन
से प्रदत्त फलन 
(i) निरंतर वर्धमान है (ii) निरंतर ह्रासमान है - अंतराल ज्ञात कीजिए जिनमें
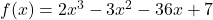 से प्रदत्त फलन
से प्रदत्त फलन
(i) निरंतर वर्धमान है (ii) निरंतर ह्रासमान है  का वह न्यूनतम मान ज्ञात कीजिए जिसके लिए अंतराल
का वह न्यूनतम मान ज्ञात कीजिए जिसके लिए अंतराल ![Rendered by QuickLaTeX.com [1,2]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-312416a3eb4144aa9d2eccb37b127681_l3.png) में
में 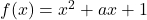 से प्रदत्त फलन निरंतर वर्धमान है।
से प्रदत्त फलन निरंतर वर्धमान है।- सिद्ध कीजिए कि फलन
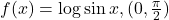 और
और 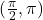 में निरंतर ह्रासमान है।
में निरंतर ह्रासमान है। - सिद्ध कीजिए कि एक शंकु के अंतर्गत महत्तम वक्रपृष्ठ वाले लंब वृत्तीय बेलन की त्रिज्या शंकु की त्रिज्या की आधी होती है।
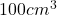 आयतन वाले डिब्बे सभी बंद बेलनाकार (लंब-वृत्तीय) डिब्बों में से न्यूनतम पृष्ठ क्षेत्रफल वाले डिब्बे की विमाएँ ज्ञात कीजिए।
आयतन वाले डिब्बे सभी बंद बेलनाकार (लंब-वृत्तीय) डिब्बों में से न्यूनतम पृष्ठ क्षेत्रफल वाले डिब्बे की विमाएँ ज्ञात कीजिए।- ऐसी दो धन संख्याएँ
 और
और  ज्ञात कीजिए ताकि
ज्ञात कीजिए ताकि 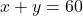 और
और 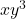 उच्चतम हो।
उच्चतम हो। - सिद्ध कीजिए कि दिए हुए पृष्ठ और महत्तम आयतन वाले लंब वृत्तीय शंकु का अर्द्ध शीर्ष कोण
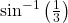 होता है।
होता है। - सिद्ध कीजिए कि
 त्रिज्या के गोले के अंतर्गत विशालतम शंकु का आयतन गोले के आयतन का
त्रिज्या के गोले के अंतर्गत विशालतम शंकु का आयतन गोले के आयतन का 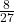 होता है।
होता है। 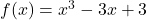 द्वारा प्रदत्त फलन के लिए स्थानीय उच्चतम और स्थानीय निम्नतम के सभी बिंदुओं को ज्ञात कीजिए।
द्वारा प्रदत्त फलन के लिए स्थानीय उच्चतम और स्थानीय निम्नतम के सभी बिंदुओं को ज्ञात कीजिए।- सिद्ध कीजिए कि न्यूनतम पृष्ठ का दिए आयतन के लंब वृत्तीय शंकु की ऊँचाई आधार की त्रिज्या की
 गुनी होती है।
गुनी होती है। - एक वृत और एक वर्ग के परिमापों का योग
 है, जहाँ
है, जहाँ  एक अचर है सिद्ध कीजिए कि उनके क्षेत्रफलों का योग निम्नतम है, जब वर्ग की भुजा वृत की त्रिज्या की दुगुनी है
एक अचर है सिद्ध कीजिए कि उनके क्षेत्रफलों का योग निम्नतम है, जब वर्ग की भुजा वृत की त्रिज्या की दुगुनी है - सिद्ध कीजिए कि दी हुई तिर्यक ऊँचाई और महत्तम आयतन वाले शंकु अर्द्ध शीर्ष कोण
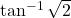 होता है।
होता है।
उत्तरः- (अध्याय-6)
प्रश्न क्रमांक-1
(i) b (ii) d (iii) c (iv) d (v) d (vi) d (vii) c (viii) a
प्रश्न क्रमांक-2
(i) 1 (ii) 1 (iii) 1 (iv) ![]() (v)
(v) ![]() , यदि
, यदि ![]()
प्रश्न क्रमांक-3
(i) ![]() (ii) निरंतर वर्धमान (iii) अधिकतम(उच्चतम) (iv)
(ii) निरंतर वर्धमान (iii) अधिकतम(उच्चतम) (iv) ![]() (v) समकोण (vi) आधी (vii) स्थानीय उच्चतम (viii) स्थानीय निम्नतम
(v) समकोण (vi) आधी (vii) स्थानीय उच्चतम (viii) स्थानीय निम्नतम
प्रश्न क्रमांक-4
(i) सत्य (ii) असत्य (iii) असत्य (iv) सत्य (v) असत्य (vi) सत्य