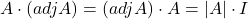mP Board 12th mathematics Determinents Question Bank :
अध्याय-4
सारणिक
प्रश्न 1. सही विकल्प चुनकर लिखिए –
- यदि
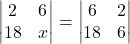 तब
तब  का मान होगा
का मान होगा - यदि
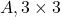 कोटि का वर्ग आव्यूह होगा तो
कोटि का वर्ग आव्यूह होगा तो 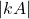
- निम्नलिखित में से कौन सा सत्य है
- यदि त्रिभुज का क्षेत्रफल 35 वर्ग इकाई है तथा इसके शीर्ष
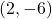
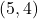 तथा
तथा 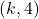 तो
तो  का मान है :
का मान है : - यदि
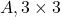 कोटि का वर्ग आव्यूह है तो
कोटि का वर्ग आव्यूह है तो 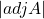 का मान है :
का मान है : - यदि
 , कोटि दो का वर्ग आव्यूह है तो
, कोटि दो का वर्ग आव्यूह है तो 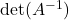 बराबर है:
बराबर है: - यदि
 और
और  दो व्युत्क्रमणीय आव्यूह है तो
दो व्युत्क्रमणीय आव्यूह है तो 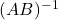 का मान बराबर है :
का मान बराबर है : - यदि
 और
और 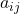 का सहखंड
का सहखंड 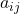 है तो
है तो  का मान निम्नलिखित रूप में व्यक्त किया जाता है |
का मान निम्नलिखित रूप में व्यक्त किया जाता है | 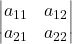 का मान है:-
का मान है:-- सारणिक
 का मान है-
का मान है- - सारणिक
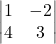 के अवयव
के अवयव 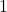 का उपसारणिक है:-
का उपसारणिक है:- - सारणिक
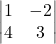 के अवयव
के अवयव 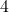 का सहखंड है:-
का सहखंड है:- - एक वर्ग आव्यूह
 व्युत्क्रमणीय कहलाता है यदि:-
व्युत्क्रमणीय कहलाता है यदि:- - एक वर्ग आव्यूह
 अव्युत्क्रमणीय कहलाता है यदि:-
अव्युत्क्रमणीय कहलाता है यदि:-
(a) ![]() (b)
(b) ![]() (c)
(c) ![]() (d)
(d) ![]()
(a) ![]() (b)
(b) ![]() (c)
(c) ![]() (d)
(d) ![]()
(a) सारणिक एक वर्ग आव्यूह है (b) सारणिक आव्यूह से संबंद्ध एक संख्या है (c) सारणिक एक वर्ग आव्यूह से सम्बद्ध एक संख्या है (d) इनमें से कोई नहीं।
(a) ![]() (b)
(b) ![]() (c)
(c) ![]() (d)
(d) ![]()
(a) ![]() (b)
(b) ![]() (c)
(c) ![]() (d)
(d) ![]()
(a) ![]() (b)
(b) ![]() (c)
(c) ![]() (d)
(d) ![]()
(a) ![]() (b)
(b) ![]() (c)
(c) ![]() (d)
(d) ![]()
(a) ![]() (b)
(b) ![]() (c)
(c) ![]() (d)
(d) ![]()
(a) ![]() (b)
(b) ![]() (c)
(c) ![]() (d)
(d) ![]()
(a) ![]() (b)
(b) ![]() (c)
(c) ![]() (d)
(d) ![]()
(a) ![]() (b)
(b) ![]() (c)
(c) ![]() (d)
(d) ![]()
(a) ![]() (b)
(b) ![]() (c)
(c) ![]() (d)
(d) ![]()
(a) ![]() (b)
(b) ![]() (c)
(c) ![]() (d)
(d) ![]()
(a) ![]() (b)
(b) ![]() (c)
(c) ![]() (d)
(d) ![]()
प्रश्न 2. एक शब्द/वाक्य में उत्तर दीजिए :
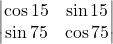 का मान क्या है ?
का मान क्या है ? के किस मान के लिए आव्यूह
के किस मान के लिए आव्यूह 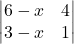 एक अव्युत्क्रमणीय आव्यूह होगा |
एक अव्युत्क्रमणीय आव्यूह होगा |- यदि
 कोई
कोई 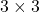 कोटि का वर्ग आव्यूह हो तब सारणिक के उपसारणिकों की संख्या लिखिए |
कोटि का वर्ग आव्यूह हो तब सारणिक के उपसारणिकों की संख्या लिखिए | - बिंदु
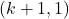
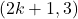 और
और 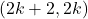 संरेख हैं तो
संरेख हैं तो  का मान क्या है ?
का मान क्या है ? 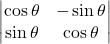 का मान ज्ञात करें |
का मान ज्ञात करें |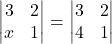 तो
तो  का मान ज्ञात करें |
का मान ज्ञात करें |- यदि किसी सारणिक की कोई पंक्ति या स्तंभ के सभी अवयव शून्य हो तो सारणिक का मान क्या होता है ?
- यदि
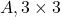 कोटि का वर्ग आव्यूह हो तो
कोटि का वर्ग आव्यूह हो तो 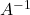 और
और 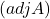 में संबंध होता है |
में संबंध होता है | - यदि
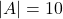 तो
तो 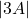 का मान क्या होगा? यदि
का मान क्या होगा? यदि 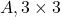 कोटि का वर्ग आव्यूह है |
कोटि का वर्ग आव्यूह है | - यदि
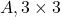 कोटि का वर्ग आव्यूह हो, तथा
कोटि का वर्ग आव्यूह हो, तथा 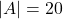 , तो
, तो 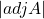 का मान क्या होगा?
का मान क्या होगा?  का मान ज्ञात करें |
का मान ज्ञात करें |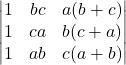 का मान क्या होगा ?
का मान क्या होगा ?- क्या
 एक व्युत्क्रमणीय आव्यूह है ?
एक व्युत्क्रमणीय आव्यूह है ?
प्रश्न 3. रिक्त स्थानों की पूर्ति कीजिए |
- सारणिक
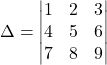 में अवयव
में अवयव 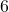 का उपसारणिक \_________\_ है |
का उपसारणिक \_________\_ है | - बिंदु
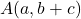 ,
, 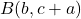 और
और 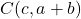 \_________\_ है |
\_________\_ है | - यदि
 कोई वर्ग आव्यूह है तथा
कोई वर्ग आव्यूह है तथा 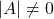 तो
तो  एक \_________\_ आव्यूह है |
एक \_________\_ आव्यूह है | - एक वर्ग आव्यूह
 अव्युत्क्रमणीय आव्यूह कहलाता है यदि \_________\_ |
अव्युत्क्रमणीय आव्यूह कहलाता है यदि \_________\_ | - यदि किसी त्रिभुज के शीर्ष के निर्देशांक
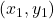 ,
, 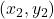 ,
, 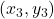 हो तो त्रिभुज का क्षेत्रफल सारणिक रूप में \_________\_ होता है |
हो तो त्रिभुज का क्षेत्रफल सारणिक रूप में \_________\_ होता है | - यदि
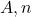 कोटि का अव्युत्क्रमणीय आव्यूह है तो
कोटि का अव्युत्क्रमणीय आव्यूह है तो 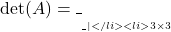 कोटि के वर्ग आव्यूह
कोटि के वर्ग आव्यूह  के लिए
के लिए 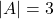 हो तो
हो तो 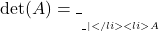 और
और  के लिए
के लिए 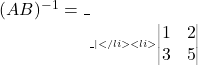 का मान \_________\_ होगा।
का मान \_________\_ होगा। - यदि
 कोटि
कोटि  का व्युत्क्रमणीय आव्यूह है तो
का व्युत्क्रमणीय आव्यूह है तो 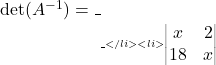 तो
तो  का मान \_________\_ होगा।
का मान \_________\_ होगा।
अध्याय-4
सारणिक
2 अंकीय प्रश्न:
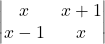 का मान ज्ञात कीजिए |
का मान ज्ञात कीजिए |- यदि
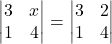 तो
तो  का मान ज्ञात कीजिए |
का मान ज्ञात कीजिए | - यदि
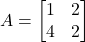 तो दिखाइए कि
तो दिखाइए कि 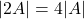 .
. - यदि
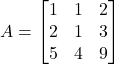 हो तो
हो तो 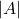 का मान ज्ञात कीजिए |
का मान ज्ञात कीजिए | - एक त्रिभुज का क्षेत्रफल ज्ञात कीजिए जिसके शीर्ष
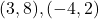 और
और 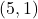 हैं |
हैं | - दर्शाइए कि
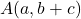 ,
, 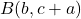 और
और 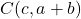 संरेख हैं |
संरेख हैं | - सारणिक
 में अवयव 4 का उपसारणिक ज्ञात कीजिए |
में अवयव 4 का उपसारणिक ज्ञात कीजिए | - सारणिक
 में अवयव 5 का सहखंड ज्ञात कीजिए |
में अवयव 5 का सहखंड ज्ञात कीजिए | - यदि
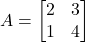 तो
तो 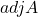 ज्ञात कीजिए |
ज्ञात कीजिए | 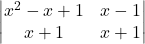 का मान ज्ञात कीजिए |
का मान ज्ञात कीजिए |- दूसरी पंक्ति के अवयवों के सहखंडों का प्रयोग करके
 का मान ज्ञात कीजिए |
का मान ज्ञात कीजिए | - यदि
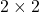 आव्यूह
आव्यूह  के लिए
के लिए 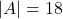 तो
तो 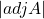 ज्ञात कीजिए |
ज्ञात कीजिए | - यदि
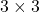 आव्यूह
आव्यूह  के लिए
के लिए 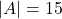 तो
तो 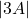 का मान ज्ञात कीजिए |
का मान ज्ञात कीजिए |
3 अंकीय प्रश्न:
- यदि
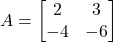 तो सत्यापित कीजिए कि
तो सत्यापित कीजिए कि 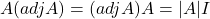
- समीकरण निकाय
![Rendered by QuickLaTeX.com \[ 5x + 2y = 4 \]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-0aac83270c7d787c56261819d1816810_l3.png)
को आव्यूह विधि से हल कीजिए |![Rendered by QuickLaTeX.com \[ 7x + 3y = 5 \]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-23310c36c2276ea79d3787e0e5ef5fac_l3.png)
 का मान ज्ञात कीजिए जबकि त्रिभुज का क्षेत्रफल 4 वर्ग इकाई है जहाँ त्रिभुज के शीर्ष
का मान ज्ञात कीजिए जबकि त्रिभुज का क्षेत्रफल 4 वर्ग इकाई है जहाँ त्रिभुज के शीर्ष 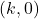 ,
, 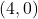 ,
, 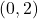 हैं |
हैं |- सारणियों का प्रयोग करके
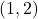 व
व 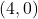 को मिलाने वाली रेखा का समीकरण ज्ञात कीजिए |
को मिलाने वाली रेखा का समीकरण ज्ञात कीजिए | 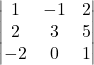 के प्रत्येक अवयव के सहखंड ज्ञात कीजिए |
के प्रत्येक अवयव के सहखंड ज्ञात कीजिए |- सारणिक
 का मान ज्ञात कीजिए |
का मान ज्ञात कीजिए | - यदि
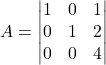 तो सिद्ध कीजिए
तो सिद्ध कीजिए 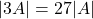
- तीसरे स्तम्भ के सहखंडों का प्रयोग करके
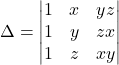 का मान ज्ञात कीजिए |
का मान ज्ञात कीजिए | 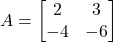 के लिए सत्यापित कीजिए कि
के लिए सत्यापित कीजिए कि 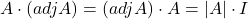
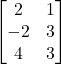 के लिए व्युत्क्रम (यदि व्युत्क्रम का अस्तित्व) ज्ञात कीजिए |
के लिए व्युत्क्रम (यदि व्युत्क्रम का अस्तित्व) ज्ञात कीजिए |
4 अंकीय प्रश्न:
- यदि
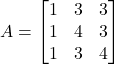 हो तो सत्यापित कीजिए कि
हो तो सत्यापित कीजिए कि 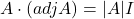 और
और 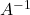 भी ज्ञात कीजिए |
भी ज्ञात कीजिए | - यदि
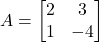
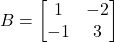 हो तो सत्यापित कीजिए कि
हो तो सत्यापित कीजिए कि 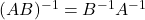
- समीकरण निकाय
![Rendered by QuickLaTeX.com \[ 3x - 2y + 3z = 8 \]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-a9e729caacec36475ee6846965aab683_l3.png)
![Rendered by QuickLaTeX.com \[ 2x + y - z = 14 \]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-f05661c78fda2f374a2491a2cf01cb42_l3.png)
को आव्यूह विधि से हल कीजिए |![Rendered by QuickLaTeX.com \[ 4x - 3y + 2z = 4 \]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-b66a6bb6f6426109371f79b71226db31_l3.png)
- सारणिकों के प्रयोग से बिन्दुओं
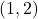 और
और 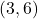 को मिलाने वाली रेखा का समीकरण ज्ञात कीजिए |
को मिलाने वाली रेखा का समीकरण ज्ञात कीजिए | - यदि
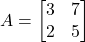 और
और 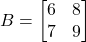 तो सिद्ध कीजिए
तो सिद्ध कीजिए 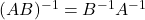
- आव्यूह
 का प्रतिलोम ज्ञात कीजिए |
का प्रतिलोम ज्ञात कीजिए | - आव्यूह
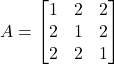 है तो सिद्ध कीजिए कि
है तो सिद्ध कीजिए कि 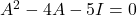 तथा
तथा 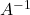 भी ज्ञात कीजिए |
भी ज्ञात कीजिए |  के लिए सत्यापित कीजिए कि
के लिए सत्यापित कीजिए कि