mP Board 12 mathematics Application of Derivatives Question Bank : mP Board 12 mathematics Application of Derivatives Question Bank is an excellent resource to aid students in their board exam preparation. यह प्रश्न बैंक अवकलज के अनुप्रयोग के महत्वपूर्ण प्रश्नों को शामिल करता है, जो कक्षा 12वीं के गणित पाठ्यक्रम का अभिन्न हिस्सा है। इसमें वस्तुनिष्ठ, लघु उत्तरीय और दीर्घ उत्तरीय प्रश्न शामिल हैं, जो छात्रों की समझ को बढ़ाते हैं। यह Text प्रारूप में उपलब्ध है, जो डाउनलोड और अभ्यास को आसान बनाता है। mP Board 12 mathematics Application of Derivatives Question Bank के साथ छात्र आत्मविश्वास और बेहतर स्कोर प्राप्त कर सकते हैं।
अध्याय-6
अवकलज के अनुप्रयोग
प्रश्न क्रमांक 1- सही विकल्प चुनकर लिखिए –
- एक वृत्त की त्रिज्या
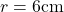 पर
पर  के सापेक्ष क्षेत्रफल में परिवर्तन की दर है:
के सापेक्ष क्षेत्रफल में परिवर्तन की दर है: - एक उत्पाद की
 इकाइयों के विक्रय से प्राप्त कुल आय रुपयों में
इकाइयों के विक्रय से प्राप्त कुल आय रुपयों में 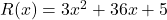 से प्रदत्त है, जब
से प्रदत्त है, जब 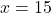 है तो सीमांत आय है:
है तो सीमांत आय है: - निम्नलिखित में कौन से फलन
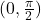 में निरंतर ह्रासमान नहीं है :
में निरंतर ह्रासमान नहीं है : - निम्नलिखित अंतरालों में से किस अंतराल में
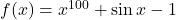 द्वारा प्रदत्त फलन
द्वारा प्रदत्त फलन  निरंतर ह्रासमान है:
निरंतर ह्रासमान है: - निम्नलिखित में से किस अंतराल में
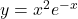 वर्धमान है ?
वर्धमान है ?  के सभी वास्तविक मानों के लिए
के सभी वास्तविक मानों के लिए  का न्यूनतम मान है:
का न्यूनतम मान है:![Rendered by QuickLaTeX.com [x(x-1)+1]^{1/3}](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-2203a3ed829055bda80249520ec8eafa_l3.png) का उच्चतम मान है:
का उच्चतम मान है:- एक
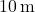 त्रिज्या के बेलनाकार टंकी में
त्रिज्या के बेलनाकार टंकी में 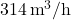 की दर से गेहूँ भरा जाता है। भरे गए गेहूँ की गहराई की वृद्धि दर है:
की दर से गेहूँ भरा जाता है। भरे गए गेहूँ की गहराई की वृद्धि दर है:
(a) ![]() (b)
(b) ![]() (c)
(c) ![]() (d)
(d) ![]()
(a) ![]() (b)
(b) ![]() (c)
(c) ![]() (d)
(d) ![]()
(a) ![]() (b)
(b) ![]() (c)
(c) ![]() (d) इनमें से कोई नहीं
(d) इनमें से कोई नहीं
(a) ![]() (b)
(b) ![]() (c)
(c) ![]() (d) इनमें से कोई नहीं
(d) इनमें से कोई नहीं
(a) ![]() (b)
(b) ![]() (c)
(c) ![]() (d)
(d) ![]()
(a) ![]() (b)
(b) ![]() (c)
(c) ![]() (d)
(d) ![]()
(a) ![]() (b)
(b) ![]() (c)
(c) ![]() (d)
(d) ![]()
(a) ![]() (b)
(b) ![]() (c)
(c) ![]() (d)
(d) ![]()
प्रश्न क्रमांक 2. एक शब्द/वाक्य में उत्तर दीजिए |
- रेखा
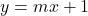 वक्र
वक्र 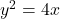 की स्पर्श रेखा है तो
की स्पर्श रेखा है तो  का मान क्या है?
का मान क्या है? ![Rendered by QuickLaTeX.com [x(x-1)+1]^{1/3}](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-2203a3ed829055bda80249520ec8eafa_l3.png) ,
, 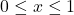 का उच्चतम मान क्या है?
का उच्चतम मान क्या है? के सभी वास्तविक मानों के लिए
के सभी वास्तविक मानों के लिए  का न्यूनतम मान क्या है?
का न्यूनतम मान क्या है?- वक्र
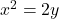 पर
पर 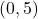 से न्यूनतम दूरी पर स्थित बिन्दु लिखिए |
से न्यूनतम दूरी पर स्थित बिन्दु लिखिए |  पर फलन
पर फलन 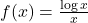 का मान उच्चतम या निम्नतम है अथवा नहीं?
का मान उच्चतम या निम्नतम है अथवा नहीं?
प्रश्न क्रमांक 3. रिक्त स्थानों की पूर्ति कीजिए |
- एक
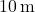 त्रिज्या के बेलनाकार टंकी में
त्रिज्या के बेलनाकार टंकी में 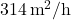 की दर से गेहूँ भरा जाता है, भरे गए गेहूँ की गहराई की वृद्धि दर \_________\_ है।
की दर से गेहूँ भरा जाता है, भरे गए गेहूँ की गहराई की वृद्धि दर \_________\_ है। - दिए हुए पृष्ठ एवं महतम आयतन के बेलन की ऊँचाई, आधार के व्यास के \_________\_ होती है |
- फलन
 के प्रान्त में एक बिंदु
के प्रान्त में एक बिंदु  जिस पर या तो
जिस पर या तो 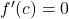 या
या  अवकलनीय नहीं है, यह बिंदु
अवकलनीय नहीं है, यह बिंदु  फलन
फलन  का \_________\_ बिंदु कहलाता है |
का \_________\_ बिंदु कहलाता है |
प्रश्न क्रमांक 4. निम्न लिखित में से सत्य/असत्य लिखिए :
- किसी उत्पाद की
 इकाइयों के विक्रय से प्राप्त कुल आय रुपयों में
इकाइयों के विक्रय से प्राप्त कुल आय रुपयों में 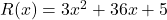 से प्रदत्त है, जब
से प्रदत्त है, जब 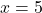 है तो सीमांत आय
है तो सीमांत आय 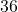 रु. होगी।
रु. होगी। - ऐसी दो धन संख्याएँ जिनका योग
 है और जिनके वर्गों का योग न्यूनतम हो तो ये संख्याएँ
है और जिनके वर्गों का योग न्यूनतम हो तो ये संख्याएँ 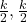 होंगी |
होंगी | - वृत्त के क्षेत्रफल के परिवर्तन की दर इसकी त्रिज्या
 के सापेक्ष
के सापेक्ष 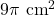 होगी जबकि
होगी जबकि 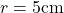
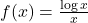 द्वारा प्रदत्त फलन
द्वारा प्रदत्त फलन  पर उच्चतम होगा |
पर उच्चतम होगा |- यदि
![Rendered by QuickLaTeX.com f, [a,b]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-eeedc8f9b53b49dc363770d49ad77ad3_l3.png) पर परिभाषित एक फलन है कि सभी
पर परिभाषित एक फलन है कि सभी 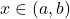 के लिए
के लिए 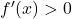 है तो
है तो 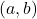 पर
पर  एक ह्रासमान फलन होगा|
एक ह्रासमान फलन होगा|
2 अंकीय प्रश्न:
- एक 5 मीटर लंबी सीढ़ी दीवार से टिकी है। सीढ़ी के निचले सिरे को दीवार से
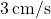 की दर से हटाया जाता है तो सीढ़ी की ऊपरी ऊँचाई किस दर से कम होगी जब इसका निचला सिरा दीवार से
की दर से हटाया जाता है तो सीढ़ी की ऊपरी ऊँचाई किस दर से कम होगी जब इसका निचला सिरा दीवार से 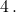 हो।
हो। - सिद्ध कीजिए कि एक दिए हुए वृत्त में खींचे गए सभी आयतों में वर्ग का क्षेत्रफल उच्चिष्ठ होता है।
- दो धनात्मक संख्याएँ
 और
और  ज्ञात कीजिए जिनका योग
ज्ञात कीजिए जिनका योग 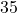 और गुणनफल महत्तम हो।
और गुणनफल महत्तम हो। - फलन
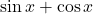 का महत्तम मान ज्ञात कीजिए।
का महत्तम मान ज्ञात कीजिए। - यदि अंतराल
![Rendered by QuickLaTeX.com [0,2]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-1571666a47302be9ed925a760be14ff0_l3.png) में
में 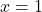 पर फलन
पर फलन  उच्चतम मान प्राप्त करता है तो
उच्चतम मान प्राप्त करता है तो  का मान ज्ञात कीजिए।
का मान ज्ञात कीजिए।
3 अंकीय प्रश्न:
- सिद्ध कीजिए
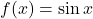 से प्रदत्त फलन
से प्रदत्त फलन
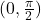 में निरंतर वर्धमान है
में निरंतर वर्धमान है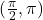 में निरंतर ह्रासमान है
में निरंतर ह्रासमान है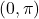 में न तो वर्धमान है और न ही ह्रासमान है |
में न तो वर्धमान है और न ही ह्रासमान है |
- अंतराल ज्ञात कीजिए जिनमें
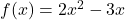 से प्रदत्त फलन
से प्रदत्त फलन 
- निरंतर वर्धमान है
- निरंतर ह्रासमान है
- अंतराल ज्ञात कीजिए जिनमें
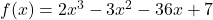 से प्रदत्त फलन
से प्रदत्त फलन 
- निरंतर वर्धमान है
- निरंतर ह्रासमान है
 का वह न्यूनतम मान ज्ञात कीजिए जिसके लिए अंतराल
का वह न्यूनतम मान ज्ञात कीजिए जिसके लिए अंतराल ![Rendered by QuickLaTeX.com [1, 2]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-6d728845b140010b5c3beb005ce31349_l3.png) में
में 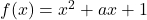 से प्रदत्त फलन निरंतर वर्धमान है।
से प्रदत्त फलन निरंतर वर्धमान है।- सिद्ध कीजिए कि फलन
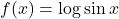 ,
, 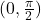 और
और 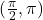 में निरंतर ह्रासमान है।
में निरंतर ह्रासमान है। - सिद्ध कीजिए कि एक शंकु के अंतर्गत महत्तम वक्रपृष्ठ वाले लंब वृत्तीय बेलन की त्रिज्या शंकु की त्रिज्या की आधी होती है।
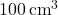 आयतन वाले डिब्बे सभी बंद बेलनाकार (लंब-वृत्तीय) डिब्बों में से न्यूनतम पृष्ठ क्षेत्रफल वाले डिब्बे की विमाएँ ज्ञात कीजिए।
आयतन वाले डिब्बे सभी बंद बेलनाकार (लंब-वृत्तीय) डिब्बों में से न्यूनतम पृष्ठ क्षेत्रफल वाले डिब्बे की विमाएँ ज्ञात कीजिए।- ऐसी दो धन संख्याएँ
 और
और  ज्ञात कीजिए ताकि
ज्ञात कीजिए ताकि 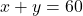 और
और 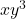 उच्चतम हो।
उच्चतम हो। 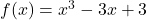 द्वारा प्रदत्त फलन के लिए स्थानीय उच्चतम और स्थानीय निम्नतम के सभी बिंदुओं को ज्ञात कीजिए।
द्वारा प्रदत्त फलन के लिए स्थानीय उच्चतम और स्थानीय निम्नतम के सभी बिंदुओं को ज्ञात कीजिए।
4 अंकीय प्रश्न:
- सिद्ध कीजिए कि दिए हुए पृष्ठ और महत्तम आयतन वाले लंब वृत्तीय शंकु का अर्ध शीर्ष कोण
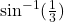 होता है।
होता है। - सिद्ध कीजिए कि
 त्रिज्या के गोले के अंतर्गत अधिकतम आयतन के बेलन की ऊँचाई
त्रिज्या के गोले के अंतर्गत अधिकतम आयतन के बेलन की ऊँचाई 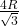 है।
है। - सिद्ध कीजिए कि
 त्रिज्या के गोले के अंतर्गत विशालतम शंकु का आयतन गोले के आयतन का
त्रिज्या के गोले के अंतर्गत विशालतम शंकु का आयतन गोले के आयतन का 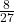 होता है।
होता है। - सिद्ध कीजिए कि न्यूनतम पृष्ठ का दिया आयतन के लंब वृत्तीय शंकु की ऊँचाई आधार की त्रिज्या की
 गुनी होती है।
गुनी होती है। - एक वृत्त और एक वर्ग के परिमापों का योग
 है, जहाँ
है, जहाँ  एक अचर है सिद्ध कीजिए कि उनके क्षेत्रफलों का योग निम्नतम है, जब वर्ग की भुजा वृत्त की त्रिज्या की दुगुनी है।
एक अचर है सिद्ध कीजिए कि उनके क्षेत्रफलों का योग निम्नतम है, जब वर्ग की भुजा वृत्त की त्रिज्या की दुगुनी है। - सिद्ध कीजिए कि दी हुई तिर्यक ऊँचाई और महत्तम आयतन वाले शंकु अर्ध शीर्ष कोण
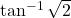 होता है।
होता है। - सिद्ध कीजिए कि
 त्रिज्या के गोले के अंतर्गत अधिकतम आयतन के बेलन की ऊँचाई
त्रिज्या के गोले के अंतर्गत अधिकतम आयतन के बेलन की ऊँचाई 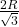 है।
है। - त्रिभुज की भुजाओं से
 और
और  दूरी पर त्रिभुज के कर्ण पर स्थित एक बिंदु है | सिद्ध कीजिए कि कर्ण की न्यूनतम लम्बाई
दूरी पर त्रिभुज के कर्ण पर स्थित एक बिंदु है | सिद्ध कीजिए कि कर्ण की न्यूनतम लम्बाई 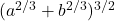 है |
है | - पानी की एक टंकी का आकार, ऊर्ध्वाधर अक्ष वाले एक उल्टे लंब वृत्तीय शंकु का जिसका शीर्ष कोण
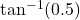 है इसमें
है इसमें 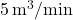 की दर से पानी भरा जाता है | पानी के स्तर बढ़ने की दर उस क्षण ज्ञात कीजिए जब टंकी में पानी की ऊँचाई
की दर से पानी भरा जाता है | पानी के स्तर बढ़ने की दर उस क्षण ज्ञात कीजिए जब टंकी में पानी की ऊँचाई 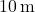 है |
है | - सिद्ध कीजिए कि
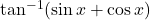 ,
, 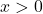 से प्रदत्त फलन
से प्रदत्त फलन  ,
, 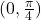 में निरंतर वर्धमान फलन है |
में निरंतर वर्धमान फलन है |
1 thought on “MP Board 12 mathematics Application of Derivatives Question Bank : कक्षा 12 गणित अवकलज के अनुप्रयोग प्रश्न बैंक”