MP Board 11th Mathematics Sets Question Bank :
अध्याय 1: समुच्चय
स्मरणीय बिंदु:
- समुच्चय और उनका निरूपण
- N: प्राकृत संख्याओं का समुच्चय
- Z: पूर्णांकों का समुच्चय
- Q: परिमेय संख्याओं का समुच्चय
- T: अपरिमेय संख्याओं का समुच्चय
- R: वास्तविक संख्याओं का समुच्चय
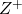 : धनात्मक पूर्णांकों का समुच्चय
: धनात्मक पूर्णांकों का समुच्चय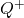 : धनात्मक परिमेय संख्याओं का समुच्चय और
: धनात्मक परिमेय संख्याओं का समुच्चय और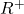 : धनात्मक वास्तविक संख्याओं का समुच्चय
: धनात्मक वास्तविक संख्याओं का समुच्चय- वस्तुओं के सुपरिभाषित संग्रह को समुच्चय कहते हैं |
- समुच्चयों को प्रायः अंग्रेजी के बड़े अक्षरों A, B, C, X, Y, Z इत्यादि से निरूपित करते हैं |
- समुच्चय के अवयवों को निरूपित करने के लिए अंग्रेजी वर्णमाला के छोटे अक्षरों a, b, c, x, y, z इत्यादि का उपयोग करते हैं |
- यदि a, समुच्चय ‘A’ का एक अवयव है तो हम
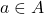 कहते हैं और यदि नहीं है तो हम
कहते हैं और यदि नहीं है तो हम 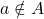 कहते हैं |
कहते हैं | - समुच्चय को निरूपित करने की दो विधियाँ हैं:(i) रोस्टर या सारणीबद्ध रूप(ii) समुच्चय निर्माण विधि
- रोस्टर रूप में सभी अवयवों को अल्पविराम से अलग करके सूचीबद्ध किया गया है और उन्हें कोष्ठक { } में रखा गया है | उदाहरण के लिए अंग्रेजी वर्णमाला में स्वर V के सेट को इस प्रकार वर्णित किया गया है :
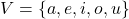
- रिक्त समुच्चय: एक समुच्चय जिसमें कोई भी अवयव नहीं होता, एक रिक्त समुच्चय कहलाता है | रिक्त समुच्चय को
 या { } से निरूपित करते हैं |
या { } से निरूपित करते हैं | - वह समुच्चय जो रिक्त हो या जिसमें निश्चित संख्या में अवयव हों, परिमित समुच्चय कहलाता है अन्यथा समुच्चय को अनंत समुच्चय कहते हैं |उदाहरण के लिए :मान लीजिए M एक वर्ष के महीनों का समुच्चय है | तब समुच्चय M एक परिमित समुच्चय है |मान लीजिए P एक रेखा के सभी बिंदुओं का समुच्चय है | तब समुच्चय P एक अपरिमित समुच्चय है |
- दो समुच्चय A और B को समान कहा जाता है, यदि उनके अवयव समान हैं और हम
 लिखते हैं |अन्यथा, समुच्चय को असमान समुच्चय कहा जाएगा और हम
लिखते हैं |अन्यथा, समुच्चय को असमान समुच्चय कहा जाएगा और हम 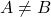 लिखते हैं |उदाहरण के लिए :माना
लिखते हैं |उदाहरण के लिए :माना 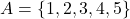 और
और 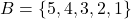 , तब
, तब  .
. - समुच्चय A को समुच्चय B का उपसमुच्चय कहा जाता है यदि A का प्रत्येक अवयव B का भी अवयव है | दूसरे शब्दों में,
 यदि जब
यदि जब 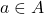 , तब
, तब 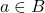 भी |उदाहरण: प्राकृत संख्याओं का समुच्चय N वास्तविक संख्याओं के समुच्चय R का एक उपसमुच्चय है, अर्थात
भी |उदाहरण: प्राकृत संख्याओं का समुच्चय N वास्तविक संख्याओं के समुच्चय R का एक उपसमुच्चय है, अर्थात 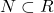 |
| - यदि A, B का उपसमुच्चय नहीं है, तो हम लिखते हैं,
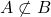 .
. - प्रत्येक समुच्चय स्वयं का एक उपसमुच्चय है | यदि A एक समुच्चय है तो
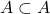 .
. 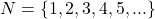
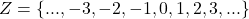
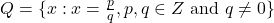
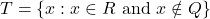
- R के उप-समुच्चय के रूप में अन्तराल
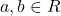 और
और 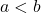 तब,
तब, - (i)
![Rendered by QuickLaTeX.com (a, b) = ]a, b[ = \{x : a < x < b\}](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-2e86f84ab8e08c8bb7c62e8f3cb13b3d_l3.png)
- (ii)
![Rendered by QuickLaTeX.com [a, b] = \{x : a \leq x \leq b\}](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-eb359afb1fc24a00056cfc255fa899c3_l3.png)
- (iii)
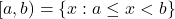
- (iv)
![Rendered by QuickLaTeX.com (a, b] = \{x : a < x \leq b\}](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-6caf54bad22f7f9843430d817c51af39_l3.png)
- वास्तविक रेखा पर R के उप-समुच्चयों के रूप में वर्णित उपर्युक्त अंतरालों को इस प्रकार दर्शाते हैं :
 को अन्तराल की लम्बाई कहते हैं |
को अन्तराल की लम्बाई कहते हैं | - समुच्चयों A और B का सम्मिलन वह समुच्चय है जिसमें A के सभी अवयवों के साथ B के भी सभी अवयव हों, तथा उभयनिष्ठ अवयवों को केवल एक बार लिया गया हो |
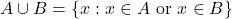 उदाहरण के लिए
उदाहरण के लिए 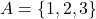 और
और 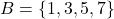 तब
तब 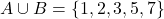 .दो समुच्चयों के सम्मिलन को आकृति में दिखाए गए वेन आरेख से प्रदर्शित किया जा सकता है :
.दो समुच्चयों के सम्मिलन को आकृति में दिखाए गए वेन आरेख से प्रदर्शित किया जा सकता है : 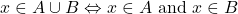 .
.- समुच्चयों A और B का सर्वनिष्ठ उन सभी अवयवों का समुच्चय है, जो A और B दोनों में उभयनिष्ठ हैं तथा उभयनिष्ठ अवयवों को केवल एक बार लिया गया हो |
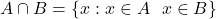 उदाहरण के लिए
उदाहरण के लिए 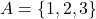 और
और 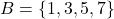 तब
तब 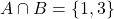 .दो समुच्चयों के सर्वनिष्ठ को आकृति में दिखाए गए वेन आरेख से प्रदर्शित किया जा सकता है :
.दो समुच्चयों के सर्वनिष्ठ को आकृति में दिखाए गए वेन आरेख से प्रदर्शित किया जा सकता है : - यदि A और B दो समुच्चय इस प्रकार हैं कि
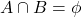 , तब A और B असंयुक्त समुच्चय कहलाते हैं |उदाहरण के लिए:
, तब A और B असंयुक्त समुच्चय कहलाते हैं |उदाहरण के लिए: 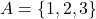 और
और 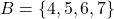 असंयुक्त समुच्चय हैं |
असंयुक्त समुच्चय हैं | 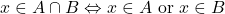 .
.- समुच्चयों A और B का अंतर उन अवयवों का समुच्चय है जो A में हैं किन्तु B में नहीं हैं, जब कि A और B को इसी क्रम में लिया जाए |
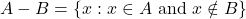 उदाहरण के लिए
उदाहरण के लिए 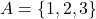 और
और 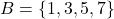 तब
तब 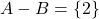 .दो समुच्चयों के अंतर को आकृति में दिखाए गए वेन आरेख से प्रदर्शित किया जा सकता है :
.दो समुच्चयों के अंतर को आकृति में दिखाए गए वेन आरेख से प्रदर्शित किया जा सकता है : - समुच्चय
 ,
,  और
और  परस्पर असंयुक्त समुच्चय होते हैं, अर्थात् इनमें से किन्हीं दो समुच्चयों का सर्वनिष्ठ एक रिक्त समुच्चय होता है |
परस्पर असंयुक्त समुच्चय होते हैं, अर्थात् इनमें से किन्हीं दो समुच्चयों का सर्वनिष्ठ एक रिक्त समुच्चय होता है | - मान लीजिए कि U सार्वत्रिक समुच्चय है और
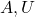 का एक उपसमुच्चय है, A का पूरक समुच्चय U के उन अवयवों का समुच्चय है, जो A के अवयव नहीं हैं | A के पूरक समुच्चय को
का एक उपसमुच्चय है, A का पूरक समुच्चय U के उन अवयवों का समुच्चय है, जो A के अवयव नहीं हैं | A के पूरक समुच्चय को  से निरूपित करते हैं |अतः
से निरूपित करते हैं |अतः 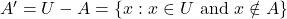 .उदाहरण के लिए: यदि
.उदाहरण के लिए: यदि 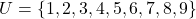 और
और 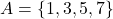 तब
तब 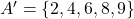 .दो समुच्चयों के अंतर को आकृति में दिखाए गए वेन आरेख से प्रदर्शित किया जा सकता है :
.दो समुच्चयों के अंतर को आकृति में दिखाए गए वेन आरेख से प्रदर्शित किया जा सकता है : 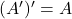
- समुच्चयों का बीजगणित के नियम
- वर्गसम नियम (i)
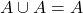 (ii)
(ii) 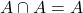
- तत्समक नियम (i)
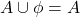 (ii)
(ii) 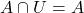 (iii)
(iii) 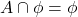 (iv)
(iv) 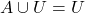
- क्रम-विनिमेय नियम (i)
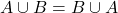 (ii)
(ii) 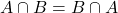
- साहचर्य नियम (i)
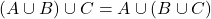 (ii)
(ii) 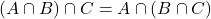
- वितरण नियम(i)
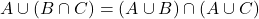 (ii)
(ii) 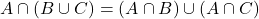 (i)
(i) 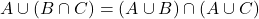 (ii)
(ii) 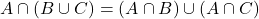
- पूरक नियम (i)
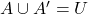 (ii)
(ii) 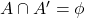 (iii)
(iii) 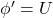 (iv)
(iv) 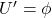
- डी-मार्गन्स नियम (i)
 (ii)
(ii)  .
. - डी-मार्गन्स नियम के अन्य रूप (i)
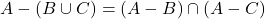 (ii)
(ii) 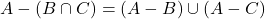
- वर्गसम नियम (i)
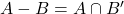
- यदि A, B और C परिमित समुच्चय हैं तब(i)
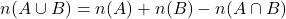 (ii)
(ii) 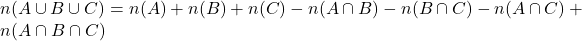
Q1. सही विकल्प चुनिये:
- किसी कक्षा में बुद्धिमान छात्रों का समुच्चय है:
(a) रिक्त समुच्चय (b) एकल समुच्चय
(c) परिमित समुच्चय (d) सुपरिभाषित संग्रह नहीं है - किसी अरिक्त समुच्चय
 के लिए
के लिए  बराबर है:
बराबर है:
(a) (b)
(b)  (c)
(c)  (d)
(d) 
- यदि
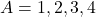 और
और 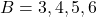 तो
तो  का मान है:
का मान है:
(a)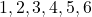 (b)
(b) 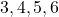 (c)
(c) 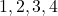 (d)
(d) 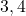
- समुच्चय
 के उपसमुच्चयों की संख्या होगी:
के उपसमुच्चयों की संख्या होगी:
(a) 1 (b) 2 (c) 3 (d) 0 - समुच्चय
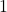 के उपसमुच्चयों की संख्या होगी:
के उपसमुच्चयों की संख्या होगी:
(a) 1 (b) 2 (c) 3 (d) 4 - समुच्चय
 तो
तो  बराबर होगा:
बराबर होगा:
(a) (b)
(b)  (c)
(c)  (d)
(d) 
- समुच्चय
 तो
तो  बराबर होगा:
बराबर होगा:
(a) (b)
(b)  (c)
(c)  (d)
(d) 
- मान लीजिए कि
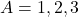 तब इसके उपसमुच्चयों की संख्या होगी :
तब इसके उपसमुच्चयों की संख्या होगी :
(a) 3 (b) 8 (c) 9 (d) 16 - समीकरण
 का हल समुच्चय रोस्टर रूप (सारणीबद्ध रूप) में होगा:
का हल समुच्चय रोस्टर रूप (सारणीबद्ध रूप) में होगा:
(a)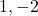 (b)
(b) 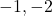 (c)
(c) 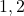 (d)
(d) 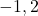
Q2. रिक्त स्थानों की पूर्ति कीजिए: - यदि
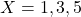 , तथा
, तथा 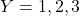 तब
तब 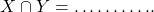
- एक समुच्चय जिसमें एक भी अवयव नहीं होता है, ……….. कहलाता है |
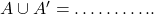
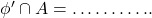
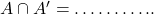
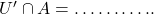


- वह समुच्चय जिसमें अवयवों की संख्या निश्चित होती है, ……….. समुच्चय कहलाता है |
- यदि
 हो तब समुच्चय
हो तब समुच्चय  और
और  ……….. समुच्चय होंगे |
……….. समुच्चय होंगे |
Q3. सही जोड़ी बनाइए:
स्तम्भ -A स्तम्भ -B
(i) (a)
(a) 
(ii) (b)
(b) 
(iii) (c)
(c) 
(iv) (d)
(d) 
(v) (e)
(e) 
Q4. एक शब्द या वाक्य में उत्तर लिखिए:
- यदि समुच्चय A में n अवयव हों तो समुच्चय A के कितने उपसमुच्चय होंगे |
- यदि
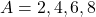 और
और 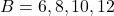 तो
तो  ज्ञात कीजिए |
ज्ञात कीजिए | - यदि
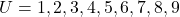 और
और 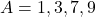 तो
तो  का पूरक समुच्चय
का पूरक समुच्चय 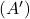 लिखिए |
लिखिए | - समीकरण
 का हल समुच्चय रोस्टर रूप में लिखिए |
का हल समुच्चय रोस्टर रूप में लिखिए | - यदि
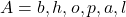 और
और 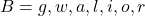 तो
तो  ज्ञात कीजिए |
ज्ञात कीजिए | - यदि
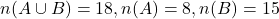 तब
तब 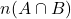 का मान लिखिए |
का मान लिखिए | - यदि
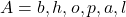 और
और 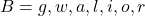 तो
तो  ज्ञात कीजिए |
ज्ञात कीजिए | - यदि
 और
और  दो असंयुक्त समुच्चय हैं तो
दो असंयुक्त समुच्चय हैं तो  में कितने अवयव होंगे |
में कितने अवयव होंगे | - यदि
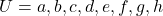 और
और 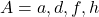 तो
तो  लिखिए |
लिखिए |
Q5. सत्य / असत्य लिखिए: - यदि
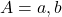 तथा
तथा 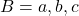 तो
तो  .
. 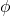 एक रिक्त समुच्चय है |
एक रिक्त समुच्चय है |- परिमित समुच्चय में अवयवों की संख्या निश्चित होती है |
- अपरिमित समुच्चय में अवयवों की संख्या निश्चित होती है |
 , सत्य है, जहाँ
, सत्य है, जहाँ  एक रिक्त समुच्चय एवं
एक रिक्त समुच्चय एवं  कोई भी परिमित समुच्चय है |
कोई भी परिमित समुच्चय है |
Q6. समुच्चय ![]() को समुच्चय निर्माण रूप में लिखिए |
को समुच्चय निर्माण रूप में लिखिए |
Q7. समान समुच्चय को उदाहरण सहित समझाइए |
Q8. अन्तराल ![]() को समुच्चय निर्माण रूप में लिखिए |
को समुच्चय निर्माण रूप में लिखिए |
Q9. समुच्चय ![]() एक सार्वत्रिक समुच्चय है, जिसके
एक सार्वत्रिक समुच्चय है, जिसके ![]() और
और ![]() उपसमुच्चय हैं | इन्हें वेन आरेख द्वारा प्रदर्शित कीजिए |
उपसमुच्चय हैं | इन्हें वेन आरेख द्वारा प्रदर्शित कीजिए |
Q10. यदि ![]() और
और ![]() तो
तो ![]() और
और ![]() ज्ञात कीजिए |
ज्ञात कीजिए |
Q11. असंयुक्त समुच्चय किसे कहते हैं | उदाहरण सहित लिखिए |
Q12. यदि ![]() तथा
तथा ![]() तो
तो ![]() तथा
तथा ![]() के मान ज्ञात कीजिए |
के मान ज्ञात कीजिए |
Q13. समुच्चय ![]() के सभी उपसमुच्चय लिखिए |
के सभी उपसमुच्चय लिखिए |
Q14. ![]() का वेन आरेख खींचिए |
का वेन आरेख खींचिए |
Q15. ![]() का वेन आरेख खींचिए |
का वेन आरेख खींचिए |
Q16. ![]() का वेन आरेख खींचिए |
का वेन आरेख खींचिए |
Q17. ![]() का वेन आरेख खींचिए |
का वेन आरेख खींचिए |
Q18. यदि ![]() और
और ![]() दो ऐसे समुच्चय हैं कि
दो ऐसे समुच्चय हैं कि ![]() में 50 अवयव हैं,
में 50 अवयव हैं, ![]() में 28 अवयव हैं और
में 28 अवयव हैं और ![]() में 32 अवयव हैं, तो
में 32 अवयव हैं, तो ![]() में कितने अवयव हैं?
में कितने अवयव हैं?
Q19. यदि ![]() और
और ![]() दो ऐसे समुच्चय हैं कि
दो ऐसे समुच्चय हैं कि ![]() तथा
तथा ![]() , हो तो
, हो तो ![]() ज्ञात कीजिए |
ज्ञात कीजिए |
Q20. यदि ![]() और
और ![]() दो समुच्चय हों
दो समुच्चय हों ![]() और
और ![]() को वेन आरेख द्वारा प्रदर्शित कीजिए |
को वेन आरेख द्वारा प्रदर्शित कीजिए |
Q21. समुच्चयों के गुणधर्मों का उपयोग करके सिद्ध कीजिए कि ![]() .
.
Q22. यदि ![]() तो
तो ![]() तथा
तथा ![]() के मान ज्ञात कीजिए |
के मान ज्ञात कीजिए |
Q23. यदि ![]() और
और ![]() तो सत्यापित कीजिए कि
तो सत्यापित कीजिए कि ![]() |
|
Q24. यदि ![]() और
और ![]() तो सत्यापित कीजिए कि
तो सत्यापित कीजिए कि ![]() |
|
Q25. एक विद्यालय में 20 अध्यापक हैं जो गणित या भौतिकी पढ़ाते हैं | इनमें से 12 गणित पढ़ाते हैं और 4 भौतिकी और गणित दोनों पढ़ाते हैं | कितने अध्यापक भौतिकी पढ़ाते हैं?
Q26. 35 विद्यार्थियों की एक कक्षा में, 24 क्रिकेट खेलना पसंद करते हैं और 16 फुटबाल खेलना पसंद करते हैं | इसके अतिरिक्त प्रत्येक विद्यार्थी कम से कम एक खेल अवश्य खेलना पसंद करता है | कितने विद्यार्थी क्रिकेट और फुटबाल दोनों खेलना पसंद करते हैं?
Q27. 400 व्यक्तियों के समूह में, 250 हिन्दी तथा 200 अंग्रेजी बोल सकते हैं | कितने व्यक्ति हिन्दी तथा अंग्रेजी दोनों बोल सकते हैं |
Q28. 70 व्यक्तियों के समूह में, 37 कॉफी, 52 चाय पसंद करते हैं और प्रत्येक व्यक्ति दोनों में से कम से कम एक पेय पसंद करता है, तो कितने व्यक्ति कॉफी और चाय दोनों को पसंद करते हैं?
Q29. एक कमेटी में, 50 व्यक्ति फ्रेंच, 20 व्यक्ति स्पेनिश और 10 व्यक्ति स्पेनिश और फ्रेंच दोनों ही भाषाओं को बोल सकते हैं | कितने व्यक्ति इन दोनों ही भाषाओं में से कम से कम एक भाषा बोल सकते हैं?
Q30. किसी स्कूल के 400 विद्यार्थियों के सर्वेक्षण में 100 विद्यार्थी सेब का रस, 150 विद्यार्थी संतरे का रस और 75 विद्यार्थी सेब तथा संतरे दोनों का रस पीने वाले पाए जाते हैं | ज्ञात कीजिए कि कितने विद्यार्थी न तो सेब का रस पीते हैं और न ही संतरे का?
Q31. 200 व्यक्ति किसी चर्म रोग से पीड़ित हैं, इनमें 120 व्यक्ति रसायन ![]() , 50 व्यक्ति रसायन
, 50 व्यक्ति रसायन ![]() , और 30 व्यक्ति रसायन
, और 30 व्यक्ति रसायन ![]() और
और ![]() दोनों ही से प्रभावित हुए हैं, तो ऐसे व्यक्तियों की संख्या ज्ञात कीजिए जो प्रभावित हुए हों:
दोनों ही से प्रभावित हुए हैं, तो ऐसे व्यक्तियों की संख्या ज्ञात कीजिए जो प्रभावित हुए हों:
(i) रसायन ![]() किन्तु रसायन
किन्तु रसायन ![]() से नहीं,
से नहीं,
(ii) रसायन ![]() किन्तु रसायन
किन्तु रसायन ![]() से नहीं
से नहीं
(iii) रसायन ![]() अथवा रसायन
अथवा रसायन ![]() से प्रभावित हुए हैं |
से प्रभावित हुए हैं |
Q32. 65 व्यक्तियों के समूह में, 40 व्यक्ति क्रिकेट, और 10 व्यक्ति क्रिकेट तथा टेनिस दोनों को पसंद करते हैं, तो कितने व्यक्ति केवल टेनिस को पसंद करते हैं किन्तु क्रिकेट को नहीं? कितने व्यक्ति टेनिस को पसंद करते हैं?
Q33. किसी विद्यालय के 600 विद्यार्थियों के सर्वेक्षण से ज्ञात हुआ कि 150 विद्यार्थी चाय, 225 विद्यार्थी कॉफी तथा 100 विद्यार्थी चाय और कॉफी दोनों पीते हैं | ज्ञात कीजिए कि कितने विद्यार्थी न तो चाय पीते हैं और न कॉफी पीते हैं |
उत्तरमाला
(वस्तुनिष्ठ प्रश्न)
A1. 1. (d) सुपरिभाषित संग्रह नहीं है 2. (b) ![]() 3. (d)
3. (d) ![]() 4. (a) 1
4. (a) 1
- (b) 2 6. (c)
 7. (b)
7. (b)  8. (b) 8 9. (a)
8. (b) 8 9. (a) 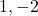
A2. 1.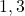 2. रिक्त समुच्चय 3.
2. रिक्त समुच्चय 3.  4.
4.  5.
5.  6.
6. 
 8.
8.  9. परिमित 10. समान
9. परिमित 10. समान
उ. 3 (i)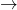 (b), (ii)
(b), (ii) 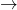 (c), (iii)
(c), (iii) 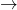 (d), (iv)
(d), (iv) 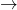 (e), (v)
(e), (v) 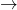 (a)
(a)
A4. 1.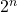 2.
2. 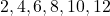 3.
3. 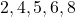
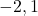 5.
5. 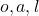 6. 5
6. 5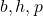 8. 0 9.
8. 0 9. 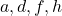
A5. 1. सत्य 2. असत्य 3. सत्य 4. असत्य 5. सत्य