MP Board 11th Mathematics Quarterly Exam 2025-26 Question Bank : MP Board 11th Mathematics Quarterly Exam 2025-26 की तैयारी के लिए सर्वश्रेष्ठ MP Board 11th Mathematics Quarterly Exam 2025-26 Question Bank यहाँ उपलब्ध है! परीक्षा में 95% से अधिक अंक लाने का सपना अब सच होगा। इस विशेष MP Board 11th Mathematics Quarterly Exam 2025-26 Question Bank में नवीनतम पाठ्यक्रम और परीक्षा पैटर्न पर आधारित सभी महत्वपूर्ण प्रश्न, उनके विस्तृत हल और टॉपर के सीक्रेट टिप्स शामिल हैं। यह आपके लिए गणित के कठिन अध्यायों जैसे समुच्चय, संबंध एवं फलन, त्रिकोणमितीय फलन और रैखिक असमिकाएं को आसान बना देगा। यह सिर्फ एक MP Board 11th Mathematics Quarterly Exam 2025-26 Question Bank नहीं बल्कि आपकी सफलता की गारंटी है। इसे अभी डाउनलोड करें और अपनी तैयारी को नई दिशा दें।

त्रैमासिक परीक्षा 2025-26
ब्लूप्रिंट
कक्षा: 11वीं
विषय: गणित
समय: 3:00 घंटे पूर्णांक: 80

प्रश्न पत्र का प्रारूप
- प्रश्न क्रमांक 1 से 5 तक 32 वस्तुनिष्ठ प्रश्न होंगे। प्रत्येक प्रश्न पर 01 अंक निर्धारित है।
- प्रश्न क्र. 1 – सही विकल्प 06, प्रश्न क्र. 2 – रिक्त स्थान 06, प्रश्न क्र. 3 – सत्य असत्य 06, प्रश्न क्र. 4 – सही जोड़ी 07, प्रश्न क्र. 5 – एक वाक्य में उत्तर 07
- नोट: “प्रश्न क्र. 4 – सही जोड़ी” के प्रश्न तैयार करते समय ध्यान रखें कि स्तंभ-A (Column A) में जो प्रश्न या कथन दिए गए हैं, उनके सही और संबंधित उत्तर प्रश्न बैंक से खोजकर स्तंभ-B (Column B) में रखें, फिर स्तंभ-B का क्रम बदल दें ताकि विद्यार्थियों को सीधे-सीधे क्रम में उत्तर न मिल पाएं और उसे मिलान करना पड़े।
- प्रश्न क्रमांक 6 से 15 तक कुल 10 प्रश्न होंगे। प्रत्येक प्रश्न पर 02 अंक निर्धारित हैं।
- प्रश्न क्रमांक 16 से 19 तक कुल 04 प्रश्न होंगे। प्रत्येक प्रश्न पर 03 अंक निर्धारित हैं।
- प्रश्न क्रमांक 20 से 23 तक कुल 04 प्रश्न होंगे। प्रत्येक प्रश्न पर 04 अंक निर्धारित हैं।
अध्याय 1: समुच्चय
1 अंक वाले प्रश्न
- किसी कक्षा में बुद्धिमान छात्रों का समुच्चय है:
(a) रिक्त समुच्चय (b) एकक समुच्चय (c) परिमित समुच्चय (d) सुपरिभाषित संग्रह नहीं है - किसी अरिक्त समुच्चय
 के लिए
के लिए  बराबर है:
बराबर है:
(a) (b)
(b)  (c)
(c)  (d)
(d) 
- यदि
 और
और  तो
तो  का मान है:
का मान है:
(a)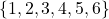 (b)
(b)  (c)
(c)  (d)
(d) 
- समुच्चय
 के उपसमुच्चयों की संख्या होगी:
के उपसमुच्चयों की संख्या होगी:
(a)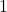 (b)
(b)  (c)
(c) 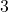 (d)
(d) 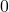
- समुच्चय
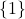 के उपसमुच्चयों की संख्या होगी:
के उपसमुच्चयों की संख्या होगी:
(a)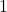 (b)
(b)  (c)
(c) 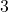 (d)
(d) 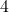
- समुच्चय
 तो
तो  बराबर होगा:
बराबर होगा:
(a) (b)
(b)  (c)
(c)  (d)
(d) 
- समुच्चय
 तो
तो  बराबर होगा:
बराबर होगा:
(a) (b)
(b)  (c)
(c)  (d)
(d) 
- मान लीजिए कि
 तब इसके उपसमुच्चयों की संख्या होगी:
तब इसके उपसमुच्चयों की संख्या होगी:
(a)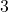 (b)
(b)  (c)
(c) 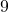 (d)
(d) 
- समीकरण
 का हल समुच्चय रोस्टर रूप (सारणीबद्ध रूप) में होगा:
का हल समुच्चय रोस्टर रूप (सारणीबद्ध रूप) में होगा:
(a) (b)
(b)  (c)
(c)  (d)
(d) 
Q2. रिक्त स्थानों की पूर्ति कीजिए:
- यदि
 तथा
तथा  तब
तब 
- एक समुच्चय जिसमें एक भी अवयव नहीं होता है,
 कहलाता है।
कहलाता है। 





- वह समुच्चय जिसमें अवयवों की संख्या निश्चित होती है,
 समुच्चय कहलाता है।
समुच्चय कहलाता है।
Q3. सत्य / असत्य लिखिए :
- यदि
 तथा
तथा  तो
तो  .
.  एक रिक्त समुच्चय है।
एक रिक्त समुच्चय है।- परिमित समुच्चय में अवयवों की संख्या निश्चित होती है।
- अपरिमित समुच्चय में अवयवों की संख्या निश्चित होती है।
 , सत्य है, जहाँ
, सत्य है, जहाँ  एक रिक्त समुच्चय एवं
एक रिक्त समुच्चय एवं  कोई भी परिमित समुच्चय है।
कोई भी परिमित समुच्चय है।
Q4. सही जोड़ी बनाइए :
| स्तम्भ -A | स्तम्भ -B |
|---|---|
| (i) | (a) |
| (ii) | (b) |
| (iii) | (c) |
| (iv) | (d) |
| (v) | (e) |
Q5. एक शब्द या वाक्य में उत्तर लिखिए:
- यदि समुच्चय
 में
में  अवयव हो तो समुच्चय
अवयव हो तो समुच्चय  के कितने उपसमुच्चय होंगे।
के कितने उपसमुच्चय होंगे। - यदि
 और
और  तो
तो  ज्ञात कीजिए।
ज्ञात कीजिए। - यदि
 और
और  तो
तो  का पूरक समुच्चय
का पूरक समुच्चय  लिखिए।
लिखिए। - समीकरण
 का हल समुच्चय रोस्टर रूप में लिखिए।
का हल समुच्चय रोस्टर रूप में लिखिए। - यदि
 और
और  तो
तो  ज्ञात कीजिए।
ज्ञात कीजिए। - यदि
 और
और  तो
तो  ज्ञात कीजिए।
ज्ञात कीजिए। - यदि
 और
और  दो असंयुक्त समुच्चय हैं तो
दो असंयुक्त समुच्चय हैं तो  में कितने अवयव होंगे।
में कितने अवयव होंगे। - यदि
 और
और  तो
तो  लिखिए।
लिखिए।
2 अंक वाले प्रश्न
- समुच्चय
 को समुच्चय निर्माण रूप में लिखिए।
को समुच्चय निर्माण रूप में लिखिए। - समान समुच्चय को उदाहरण सहित समझाइए।
- अन्तराल
![Rendered by QuickLaTeX.com [6,12]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-99e7b2b1ad00b4b3292c41f9918906cd_l3.png) को समुच्चय निर्माण रूप में लिखिए।
को समुच्चय निर्माण रूप में लिखिए। - समुच्चय
 एक सार्वत्रिक समुच्चय है, जिसके
एक सार्वत्रिक समुच्चय है, जिसके  और
और  उपसमुच्चय हैं। इन्हें वेन आरेख द्वारा प्रदर्शित कीजिए।
उपसमुच्चय हैं। इन्हें वेन आरेख द्वारा प्रदर्शित कीजिए। - यदि
 और
और  तो
तो  और
और  ज्ञात कीजिए।
ज्ञात कीजिए। - असंयुक्त समुच्चय किसे कहते हैं। उदाहरण सहित लिखिए।
- यदि
 तथा
तथा  तो
तो  तथा
तथा  के मान ज्ञात कीजिए।
के मान ज्ञात कीजिए। - समुच्चय
 के सभी उपसमुच्चय लिखिए।
के सभी उपसमुच्चय लिखिए।  का वेन आरेख खींचिए।
का वेन आरेख खींचिए। का वेन आरेख खींचिए।
का वेन आरेख खींचिए। का वेन आरेख खींचिए।
का वेन आरेख खींचिए। का वेन आरेख खींचिए।
का वेन आरेख खींचिए।- यदि
 और
और  दो समुच्चय हों और
दो समुच्चय हों और  और
और  को वेन आरेख द्वारा प्रदर्शित कीजिए।
को वेन आरेख द्वारा प्रदर्शित कीजिए। - यदि
 ,
,  ,
,  तो
तो  तथा
तथा  के मान ज्ञात कीजिए।
के मान ज्ञात कीजिए।
3 अंक वाले प्रश्न
- निम्नलिखित को अन्तराल के रूप में लिखिए :
(i)
(ii)
(iii)
- निम्नलिखित को अन्तरालों को समुच्चय निर्माण रूप में लिखिए :
(i)
(ii)![Rendered by QuickLaTeX.com [7,13]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-095ca83d6297cc628ce2cff20b0cba90_l3.png)
(iii)![Rendered by QuickLaTeX.com (7,11]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-a31649f830679cdfdcb0e8699788ce23_l3.png)
- निम्नलिखित समुच्चयों को रोस्टर रूप में लिखिए :
(i) एक पूर्णांक है और
एक पूर्णांक है और 
(ii) संख्या 7 से कम एक प्राकृत संख्या है
संख्या 7 से कम एक प्राकृत संख्या है
(iii) एक अभाज्य संख्या है जो संख्या 60 की विभाजक है
एक अभाज्य संख्या है जो संख्या 60 की विभाजक है
- दिखाइए कि शब्द “CATARACT” के वर्ण विन्यास के अक्षरों का समुच्चय तथा शब्द “TRACT” के वर्णविन्यास के अक्षरों का समुच्चय समान है।
- सिद्ध कीजिए कि
 का तात्पर्य है कि
का तात्पर्य है कि  .
. - ऐसे समुच्चय
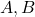 और
और  ज्ञात कीजिए ताकि
ज्ञात कीजिए ताकि  ,
,  तथा
तथा  अरिक्त समुच्चय हों और
अरिक्त समुच्चय हों और  .
.
4 अंक वाले प्रश्न
- यदि
 ,
,  और
और  तो सत्यापित कीजिए कि
तो सत्यापित कीजिए कि  .
. - यदि
 ,
,  और
और  तो सत्यापित कीजिए कि
तो सत्यापित कीजिए कि  .
. - मान लीजिए कि
 और
और  समुच्चय हैं। यदि किसी समुच्चय
समुच्चय हैं। यदि किसी समुच्चय 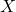 के लिए
के लिए  तथा
तथा  , तो सिद्ध कीजिए कि
, तो सिद्ध कीजिए कि  .
. - मान लीजिए
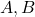 और
और  ऐसे समुच्चय हैं कि
ऐसे समुच्चय हैं कि  तथा
तथा  , तो दर्शाइए कि
, तो दर्शाइए कि  .
. - मान लीजिए कि
 और
और  समुच्चय हैं। यदि किसी समुच्चय
समुच्चय हैं। यदि किसी समुच्चय 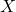 के लिए
के लिए  तथा
तथा  , तो सिद्ध कीजिए कि
, तो सिद्ध कीजिए कि  .
. - किन्हीं दो समुच्चयों
 तथा
तथा  के लिए सिद्ध कीजिए कि
के लिए सिद्ध कीजिए कि  .
. - किन्हीं दो समुच्चयों
 तथा
तथा  के लिए सिद्ध कीजिए कि
के लिए सिद्ध कीजिए कि  .
.
अध्याय 2: संबंध एवं फलन
1 अंक वाले प्रश्न
- सही विकल्प चुनिए:
- फलन
 कहलाता है:
कहलाता है:
(a) तत्समक फलन (b) अचर फलन (c) मापांक फलन (d) चिन्ह फलन - फलन
 , जहाँ
, जहाँ  एक अचर है, कहलाता है:
एक अचर है, कहलाता है:
(a) तत्समक फलन (b) अचर फलन (c) मापांक फलन (d) चिन्ह फलन - फलन
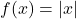 कहलाता है:
कहलाता है:
(a) तत्समक फलन (b) अचर फलन (c) मापांक फलन (d) चिन्ह फलन - यदि
 तो
तो  व
व  के मान क्रमशः होंगे:
के मान क्रमशः होंगे:
(a) (b)
(b)  (c)
(c)  (d)
(d) 
- यदि
 और
और  तो
तो  से
से  पर संबंधों की संख्या होगी:
पर संबंधों की संख्या होगी:
(a) (b)
(b) 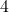 (c)
(c)  (d)
(d) 
- दो परिमित समुच्चय
 तथा
तथा  इस प्रकार हैं कि
इस प्रकार हैं कि  ,
,  तब
तब  से
से  में संबंधों की संख्या होगी:
में संबंधों की संख्या होगी:
(a) (b)
(b) 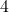 (c)
(c)  (d)
(d) 
- यदि
 तथा
तथा  दो समुच्चय हैं, तब
दो समुच्चय हैं, तब  यदि और केवल यदि
यदि और केवल यदि
(a) (b)
(b)  (c)
(c)  (d)
(d) 
Q2. रिक्त स्थानों की पूर्ति कीजिए:

- यदि
 या
या  में से कोई अपरिमित समुच्चय है तो
में से कोई अपरिमित समुच्चय है तो 
 समुच्चय होता है।
समुच्चय होता है। - किसी अरिक्त समुच्चय
 से अरिक्त समुच्चय
से अरिक्त समुच्चय  में संबंध
में संबंध  , कार्तीय गुणन
, कार्तीय गुणन  का
का  होता है।
होता है। - किसी अरिक्त समुच्चय
 से अरिक्त समुच्चय
से अरिक्त समुच्चय  में संबंध
में संबंध  के सभी क्रमित युग्मों के प्रथम घटकों के समुच्चय को संबंध
के सभी क्रमित युग्मों के प्रथम घटकों के समुच्चय को संबंध  का
का  कहते हैं।
कहते हैं।
Q3. सही जोड़ी बनाइए:
| स्तम्भ -A | स्तम्भ -B |
|---|---|
| (i) | (a) |
| (ii) | (b) तत्समक फलन |
(iii)  | (c) मापांक फलन |
| (iv) | (d) चिन्ह फलन |
| (v) | (e) महत्तम पूर्णांक फलन |
Q4. एक शब्द या वाक्य में उत्तर लिखिए:
- यदि
 और
और  तो समुच्चय
तो समुच्चय  ज्ञात कीजिए।
ज्ञात कीजिए। - एक फलन
 द्वारा परिभाषित है तो
द्वारा परिभाषित है तो  का मान लिखिए।
का मान लिखिए। - यदि
 और
और  तो
तो  से
से  में संबंधों की संख्या कितनी होगी?
में संबंधों की संख्या कितनी होगी? - यदि
 तथा
तथा  तो
तो  क्या होगा?
क्या होगा?
Q5. सत्य / असत्य लिखिए :


- दो क्रमित युग्म समान होते हैं, यदि और केवल यदि उनके संगत प्रथम घटक समान हों और संगत द्वितीय घटक भी समान हों।
 , यहाँ
, यहाँ  एक क्रमित त्रिक कहलाता है।
एक क्रमित त्रिक कहलाता है।- किसी संबंध
 का परिसर (Range) उस संबंध के सह-प्रांत (Co-domain) का उपसमुच्चय (Subset) होता है, अर्थात् परिसर (Range)
का परिसर (Range) उस संबंध के सह-प्रांत (Co-domain) का उपसमुच्चय (Subset) होता है, अर्थात् परिसर (Range) सह-प्रांत (Co-domain)।
सह-प्रांत (Co-domain)। - यदि
 तथा
तथा  तो
तो  तथा
तथा  से
से  में संबंधों की कुल संख्या
में संबंधों की कुल संख्या  .
.
2 अंक वाले प्रश्न
- यदि
 क्रमशः:
क्रमशः:  ,
,  द्वारा परिभाषित हैं।
द्वारा परिभाषित हैं। 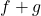 और
और  ज्ञात कीजिए।
ज्ञात कीजिए। - यदि
 क्रमशः:
क्रमशः:  ,
,  द्वारा परिभाषित है।
द्वारा परिभाषित है।  और
और  ज्ञात कीजिए।
ज्ञात कीजिए। - यदि
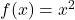 तथा
तथा  हो तो
हो तो  और
और  ज्ञात कीजिए।
ज्ञात कीजिए। - यदि
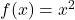 तथा
तथा  हो तो
हो तो  और
और  ज्ञात कीजिए।
ज्ञात कीजिए। - यदि
 तथा
तथा  , ऋणेत्तर वास्तविक संख्याओं के लिए परिभाषित दो फलन है तो
, ऋणेत्तर वास्तविक संख्याओं के लिए परिभाषित दो फलन है तो  और
और  ज्ञात कीजिए।
ज्ञात कीजिए। - यदि
 तथा
तथा  , ऋणेत्तर वास्तविक संख्याओं के लिए परिभाषित दो फलन है तो
, ऋणेत्तर वास्तविक संख्याओं के लिए परिभाषित दो फलन है तो  और
और  ज्ञात कीजिए।
ज्ञात कीजिए। - यदि
 ,
,  ,
,  तथा
तथा  , सत्यापित कीजिए कि
, सत्यापित कीजिए कि  ,
,  का एक उपसमुच्चय है।
का एक उपसमुच्चय है।
3 अंक वाले प्रश्न
- फलन
 का प्रांत (Domain) तथा परिसर (Range) ज्ञात कीजिए।
का प्रांत (Domain) तथा परिसर (Range) ज्ञात कीजिए। - फलन
 द्वारा परिभाषित वास्तविक फलन
द्वारा परिभाषित वास्तविक फलन  का प्रांत (Domain) तथा परिसर (Range) ज्ञात कीजिए।
का प्रांत (Domain) तथा परिसर (Range) ज्ञात कीजिए। - यदि
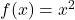 हो तो
हो तो  का मान ज्ञात कीजिए।
का मान ज्ञात कीजिए।
4 अंक वाले प्रश्न
- यदि
 ,
,  द्वारा
द्वारा  से
से  में एक संबंध परिभाषित कीजिए। (i) इस संबंध को एक तीर आरेख द्वारा दर्शाइए। (ii)
में एक संबंध परिभाषित कीजिए। (i) इस संबंध को एक तीर आरेख द्वारा दर्शाइए। (ii)  के प्रांत, सह-प्रांत तथा परिसर लिखिए।
के प्रांत, सह-प्रांत तथा परिसर लिखिए। - यदि
 ,
,  द्वारा,
द्वारा,  से
से  का एक संबंध
का एक संबंध  लिखिए। इसके प्रांत, सह-प्रांत और परिसर लिखिए।
लिखिए। इसके प्रांत, सह-प्रांत और परिसर लिखिए। - प्राकृत संख्याओं के समुच्चय पर
 संख्या 4 से कम, एक प्राकृत संख्या है,
संख्या 4 से कम, एक प्राकृत संख्या है,  द्वारा एक संबंध
द्वारा एक संबंध  परिभाषित कीजिए। इस संबंध को (i) रोस्टर रूप में लिखिए। (ii) इसके प्रांत और परिसर लिखिए।
परिभाषित कीजिए। इस संबंध को (i) रोस्टर रूप में लिखिए। (ii) इसके प्रांत और परिसर लिखिए। - यदि
 और
और  पर
पर  संख्या
संख्या  संख्या
संख्या  को यथावत विभाजित करती है
को यथावत विभाजित करती है द्वारा परिभाषित एक संबंध है। (i)
द्वारा परिभाषित एक संबंध है। (i)  को रोस्टर रूप में लिखिए। (ii)
को रोस्टर रूप में लिखिए। (ii)  का प्रांत ज्ञात कीजिए। (iii)
का प्रांत ज्ञात कीजिए। (iii)  का परिसर ज्ञात कीजिए।
का परिसर ज्ञात कीजिए।  द्वारा परिभाषित संबंध
द्वारा परिभाषित संबंध  के प्रांत और परिसर ज्ञात कीजिए।
के प्रांत और परिसर ज्ञात कीजिए।- यदि
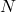 प्राकृत संख्याओं का समुच्चय है और
प्राकृत संख्याओं का समुच्चय है और 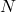 पर परिभाषित एक संबंध
पर परिभाषित एक संबंध  इस प्रकार है कि
इस प्रकार है कि  .
.  के प्रांत, सह-प्रांत और परिसर क्या हैं? क्या यह संबंध, एक फलन है?
के प्रांत, सह-प्रांत और परिसर क्या हैं? क्या यह संबंध, एक फलन है? - फलन
 का प्रांत ज्ञात कीजिए।
का प्रांत ज्ञात कीजिए। - फलन
 का प्रांत ज्ञात कीजिए।
का प्रांत ज्ञात कीजिए। - यदि
 ,
, 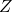 से
से 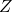 में एक रैखिक फलन है तो
में एक रैखिक फलन है तो  ज्ञात कीजिए।
ज्ञात कीजिए। - फलन ‘t’ सेल्सियस तापमान का फारेनहाइट तापमान में प्रतिचित्रण करता है, जो
 द्वारा परिभाषित है। निम्नलिखित को ज्ञात कीजिए: (i)
द्वारा परिभाषित है। निम्नलिखित को ज्ञात कीजिए: (i)  (ii)
(ii)  (iii)
(iii)  का मान जब
का मान जब  .
.
This link help me for exams notifications