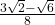MP Board 10th Trigonometry Introduction Question Bank : अध्याय 8: त्रिकोणमिति का परिचय
स्मरणीय बिंदु
- त्रिकोणमितीय अनुपात: समकोण त्रिभुज ABC में
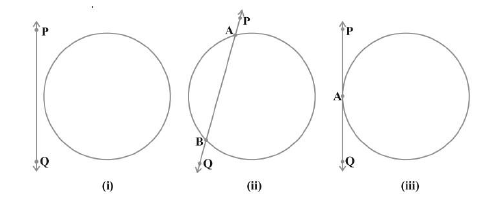
त्रिकोणमितीय अनुपात: समकोण त्रिभुज ABC में
- कर्ण: AC
- कोण A की सम्मुख भुजा: BC
- कोण A की संलग्न भुजा: AB
- मूल अनुपात:
मूल अनुपात:
![]()
![]()
![]()
- व्युत्क्रम (Reciprocal) अनुपात:
- व्युत्क्रम संबंध:
- कुछ विशिष्ट कोणों के त्रिकोणमितीय अनुपात
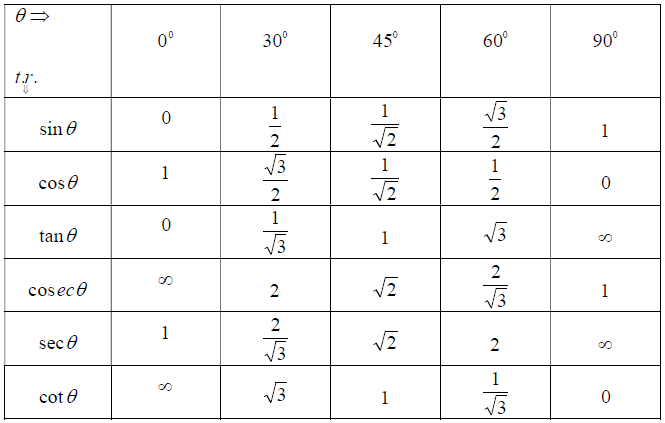
यहाँ स्कैन किया गया टेक्स्ट है:
- पूरक कोणों के त्रिकोणमितीय अनुपात
- त्रिकोणमितीय सर्वसमिकाएँ
प्र. 1 सही विकल्प चुनिए
(1) ![]() तब सत्य होगा जबकि A बराबर है:
तब सत्य होगा जबकि A बराबर है:
(अ) ![]() (ब)
(ब) ![]() (स)
(स) ![]() (द)
(द) ![]()
- हल: हम A के मानों को रखकर जाँच करेंगे:
- (अ)
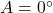 रखने पर:
रखने पर: 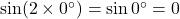 .
.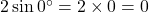 .
.
चूँकि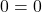 , यह सत्य है।
, यह सत्य है।
- (अ)
- सही विकल्प: (अ)

(2) ![]() का मान है:
का मान है:
(अ) ![]() (ब)
(ब) ![]() (स)
(स) ![]() (द)
(द) ![]()
- हल: यह एक मूलभूत त्रिकोणमितीय सर्वसमिका है:
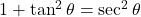 .
. - सही विकल्प: (ब)
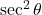
(3) ![]() =
=
(अ) ![]() (ब) 1 (स)
(ब) 1 (स) ![]() (द) 0
(द) 0
- हल:
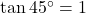 .
.
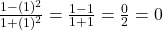 .
.
- सही विकल्प: (द) 0
(4) यदि ![]() हो तो
हो तो ![]() =
=
(अ) ![]() (ब)
(ब) ![]() (स)
(स) ![]() (द) 1
(द) 1
- हल:
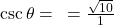 .
.
- पाइथागोरस प्रमेय से,
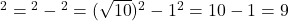 .
. 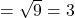 .
.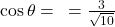 .
.
- पाइथागोरस प्रमेय से,
- सही विकल्प: (ब)
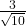
(5) ![]() =
=
(अ) 1/2 (ब) 1/3 (स) 1/4 (द) 1
- हल:
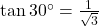 ,
,  ,
, 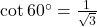 ,
, 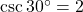 .
.
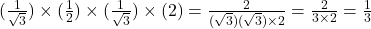 .
.
- सही विकल्प: (ब) 1/3
(6) ![]() =
=
(अ) ![]() (ब) 2 (स) 3 (द) 1
(ब) 2 (स) 3 (द) 1
- हल: पूरक कोणों के सूत्र
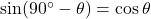 का उपयोग करने पर:
का उपयोग करने पर:
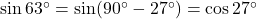 .
. .
.
- सही विकल्प: (द) 1
(7) ![]() =
=
(अ) 1 (ब) ![]() (स)
(स) ![]() (द)
(द) ![]()
- हल: सर्वसमिकाओं
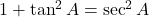 और
और 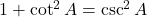 का उपयोग करने पर:
का उपयोग करने पर:
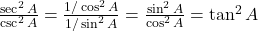 .
.
- सही विकल्प: (द)
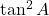
(8) ![]() =
=
(अ) 1 (ब) 8 (स) 9 (द) 0
- हल: 9 कॉमन लेने पर:
 .
.
- चूँकि
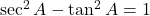 (सर्वसमिका से)।
(सर्वसमिका से)। 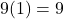 .
.
- चूँकि
- सही विकल्प: (स) 9
(9) ![]() का मान है:
का मान है:
(अ) ![]() (ब)
(ब) ![]() (स)
(स) ![]() (द)
(द) ![]()
- हल: यह पूरक कोणों का मानक सूत्र है।
 .
. - सही विकल्प: (ब)
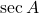
(10) यदि ![]() तो
तो ![]() का मान होगा।
का मान होगा।
(अ) 2 (ब) 1 (स) ![]() (द) 0
(द) 0
- हल:
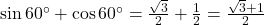 .
. - सही विकल्प: (स)
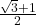
(11) ![]() का मान होगा:
का मान होगा:
(अ) 1 (ब) 1/3 (स) 0 (द) -1
- हल:
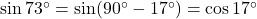 .
.
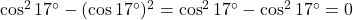 .
.
- सही विकल्प: (स) 0
(12) ![]() =
=
(अ) ![]() (ब)
(ब) ![]() (स)
(स) ![]() (द)
(द) ![]()
- हल: यह
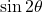 का सूत्र है,
का सूत्र है, 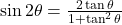 .
.
- यहाँ
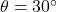 , अतः यह
, अतः यह 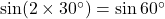 के बराबर है।
के बराबर है।
- यहाँ
- सही विकल्प: (अ)
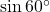
(13) ![]() =
=
(अ) ![]() (ब)
(ब) ![]() (स)
(स) ![]() (द)
(द) ![]()
- हल: अंश और हर को
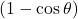 से गुणा करने पर:
से गुणा करने पर:
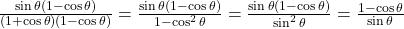 .
.
- सही विकल्प: (स)
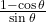
(14) ![]() का मान होगा:
का मान होगा:
(अ) ![]() (ब)
(ब) ![]() (स) 1 (द)
(स) 1 (द) ![]()
- हल: रूट के अंदर
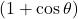 से अंश और हर में गुणा करने पर:
से अंश और हर में गुणा करने पर:
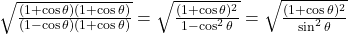
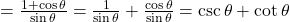 .
.
- सही विकल्प: (ब)
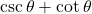
(15) ![]() बराबर है:
बराबर है:
(अ) 0 (ब) 1 (स) 2 (द) -1
- हल:
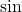 और
और  में बदलने पर:
में बदलने पर:

- ऊपर
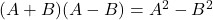 का रूप है, जहाँ
का रूप है, जहाँ 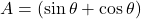 और
और 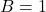 .
. 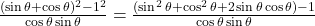
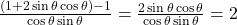 .
.
- सही विकल्प: (स) 2
(16) ![]() बराबर है:
बराबर है:
(अ) ![]() (ब) -1 (स)
(ब) -1 (स) ![]() (द)
(द) ![]()
- हल: (यह प्रश्न 7 का दोहराव है)
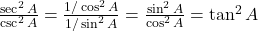 .
. - सही विकल्प: (द)
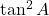
(17) ![]() बराबर है:
बराबर है:
(अ) ![]() (ब)
(ब) ![]() (स)
(स) ![]() (द)
(द) ![]()
- हल:
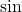 और
और  में बदलने पर:
में बदलने पर:
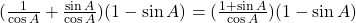
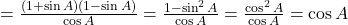 .
.
- सही विकल्प: (द)
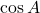
प्र. 2 रिक्त स्थानों की पूर्ति करे
(i) ![]() का मान
का मान ![]() होगा।
होगा।
- हल:
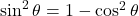 ,
, 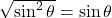 .
.
(ii) ![]() का मान 1 होगा।
का मान 1 होगा।
- हल:
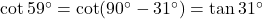 .
.
(iii) ![]() का मान
का मान ![]() होगा।
होगा।
(iv) ![]() का मान
का मान ![]() होगा।
होगा।
- हल:
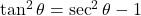 ,
, 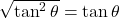 .
.
(v) ![]() का मान
का मान ![]() होगा।
होगा।
(vi) ![]() का मान 1 होगा।
का मान 1 होगा।
- हल:
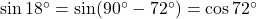 .
.
(vii) ![]() का मान -1 होगा।
का मान -1 होगा।
- हल:
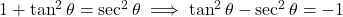 .
.
(viii) ![]() का मान
का मान ![]() होगा।
होगा।
(ix) ![]() का मान 1 होगा।
का मान 1 होगा।
- हल:
 .
.
(x) ![]() हो तो
हो तो ![]() मान
मान ![]() होगा।
होगा।
- हल:
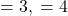 ,
, 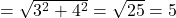 .
. 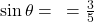 .
.
प्र.3 Match the Coloumn
1.
- (1)
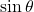 → (ii) लंब / कर्ण
→ (ii) लंब / कर्ण - (2)
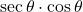 → (iii) 1
→ (iii) 1 - (3)
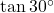 → (iv)
→ (iv) 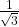
- (4)
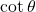 → (v)
→ (v) 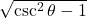
- (5)
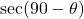 → (vi)
→ (vi) 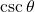
2.
- (1)
 → (iii)
→ (iii) 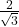
- (2)
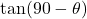 → (iv)
→ (iv) 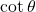
- (3)
 → (v) 2
→ (v) 2
- (हल:
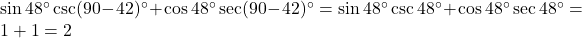 )
)
- (हल:
- (4)
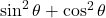 → (i) 1
→ (i) 1 - (5)
 → (ii)
→ (ii) 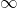 (अपरिभाषित)
(अपरिभाषित)
प्र.3 Match the Coloumn
- (1)
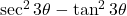 → (iii) 1
→ (iii) 1
- (हल: सर्वसमिका
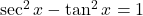 से)
से)
- (हल: सर्वसमिका
- (2)
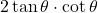 → (iv) 2
→ (iv) 2
- (हल:
 )
)
- (हल:
- (3)
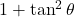 → (v)
→ (v) 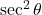
- (4)
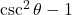 → (i)
→ (i) 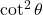
- (5)
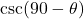 → (ii)
→ (ii) 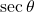
प्र.4 Match the Coloumn
- (1)
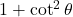 → (v)
→ (v) 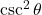
- (2)
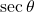 → (vi)
→ (vi) 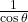
- (3)
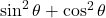 → (iv) 1
→ (iv) 1 - (4)
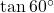 → (iii)
→ (iii) 
- (5)
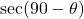 → (i)
→ (i) 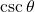
प्र.5 Match the Coloumn
- (1)
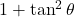 → (ii)
→ (ii) 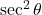
- (2)
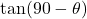 → (iv)
→ (iv) 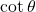
- (3)
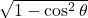 → (v)
→ (v) 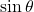
- (हल:
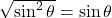 )
)
- (हल:
- (4)
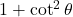 → (i)
→ (i) 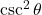
- (5)
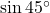 → (iii)
→ (iii) 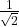
प्र.6 Match the Coloumn
- (1)
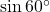 → (ii)
→ (ii) 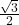
- (2)
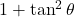 → (i)
→ (i) 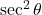
- (3)
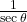 → (iv)
→ (iv) 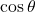
- (4)
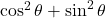 → (v) 1
→ (v) 1 - (5)
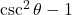 → (iii)
→ (iii) 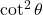
प्र.7 Match the Coloumn
- (i)
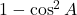 → (ब)
→ (ब) 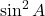
- (ii)
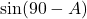 → (स)
→ (स) 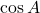
- (iii)
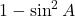 → (फ)
→ (फ) 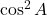
- (iv)
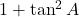 → (अ)
→ (अ) 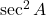
- (v)
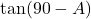 → (द)
→ (द) 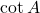
- (vi)
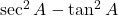 → (ई) 1
→ (ई) 1
प्र.8 Match the Coloumn
- (i)
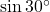 → (द)
→ (द) 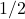
- (ii)
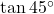 → (फ) 1
→ (फ) 1 - (iii)
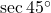 → (ई)
→ (ई) 
- (iv)
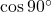 → (अ) 0
→ (अ) 0 - (v)
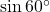 → (ब)
→ (ब) 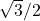
- (vi)
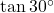 → (स)
→ (स) 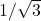
यहाँ सभी स्कैन किए गए प्रश्नों के पाठ और उनके उचित हल दिए गए हैं:
प्र.04 एक शब्द / वाक्य में उत्तर लिखिए।
(i) ![]() का मान लिखिए।
का मान लिखिए।
- हल: यह एक त्रिकोणमितीय सर्वसमिका है।
- उत्तर:
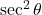
(ii) ![]() का मान लिखिए।
का मान लिखिए।
- हल: यह एक त्रिकोणमितीय सर्वसमिका है।
- उत्तर:
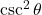
(iii) ![]() का मान लिखिए।
का मान लिखिए।
- हल: यह पूरक कोणों का सूत्र है।
- उत्तर:
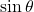
(iv) ![]() का मान लिखिए।
का मान लिखिए।
- हल: यह
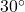 के लिए
के लिए 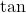 का मानक मान है।
का मानक मान है। - उत्तर:
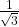
(v) ![]() का मान लिखिए।
का मान लिखिए।
- हल: यह मुख्य त्रिकोणमितीय सर्वसमिका है।
- उत्तर: 1
(vi) ![]() का मान बताइए।
का मान बताइए।
- हल:
 .
. - उत्तर:
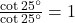
(vii) ![]() को
को ![]() और
और ![]() के बीच के कोणों में व्यक्त कीजिए।
के बीच के कोणों में व्यक्त कीजिए।
- हल:
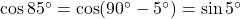 .
. 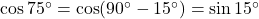 .
. - उत्तर:
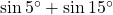
(viii) ![]() का मान क्या होगा?
का मान क्या होगा?
- हल: यह
 का सूत्र है, जो
का सूत्र है, जो 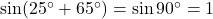 होता है।
होता है।
वैकल्पिक रूप से: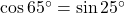 और
और 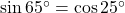 .
.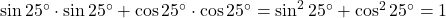 .
. - उत्तर: 1
प्र.05 सत्य/ असत्य लिखिए।
(i) ![]() के सभी मानों के लिए
के सभी मानों के लिए ![]() होता है।
होता है।
- उत्तर: असत्य (यह केवल
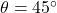 के लिए सत्य है)।
के लिए सत्य है)।
(ii) ![]() का मान सदैव 1 से कम होता है।
का मान सदैव 1 से कम होता है।
- उत्तर: असत्य (जैसे,
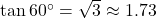 , जो 1 से अधिक है)।
, जो 1 से अधिक है)।
(iii) ![]() ,
, ![]() और
और ![]() का गुणनफल होता है।
का गुणनफल होता है।
- उत्तर: असत्य (
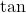 , कोण
, कोण  पर एक फलन (function) है)।
पर एक फलन (function) है)।
(iv) ![]()
- उत्तर: असत्य (यह त्रिकोणमिति का गुण नहीं है)।
(v) ![]() पर
पर ![]() परिभाषित नहीं है।
परिभाषित नहीं है।
- उत्तर: सत्य (क्योंकि
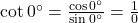 , जो अपरिभाषित है)।
, जो अपरिभाषित है)।
प्र.06 से प्र.55 (गणना एवं सिद्धि)
प्र.06 यदि ![]() हो तो
हो तो ![]() का मान क्या होगा?
का मान क्या होगा?
- हल:
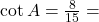 .
.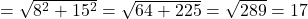 .
.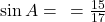 .
. - उत्तर:
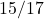
प्र.07 यदि ![]() तो
तो ![]() का मान क्या होगा?
का मान क्या होगा?
- हल:
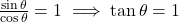 . यह
. यह  पर होता है।
पर होता है। - उत्तर:

प्र.08 ![]() किसके बराबर है?
किसके बराबर है?
- हल:
 .
. - उत्तर: 1
प्र.09 यदि ![]() हो तो
हो तो ![]() का मान क्या होगा? (माना
का मान क्या होगा? (माना ![]() )
)
- हल:
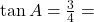 .
. 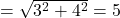 .
.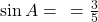 .
. - उत्तर:
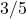
प्र.10 यदि ![]() तो
तो ![]() का मान क्या होगा?
का मान क्या होगा?
- हल:
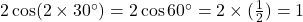 .
. - उत्तर: 1
प्र.11 ![]() का मान क्या होगा?
का मान क्या होगा?
- हल:
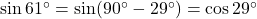 .
. - उत्तर:
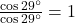
प्र.12 ![]() का मान क्या होगा?
का मान क्या होगा?
- हल:
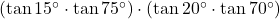
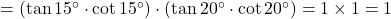 .
. - उत्तर: 1
प्र.13 यदि ![]() तब
तब ![]() का मान क्या होगा?
का मान क्या होगा?
(नोट: यह प्रश्न अधूरा या त्रुटिपूर्ण प्रतीत होता है, क्योंकि इसका उत्तर एक संख्या नहीं होगी। यदि प्रश्न ![]() होता, तो हल 8/17 होता। यदि प्रश्न
होता, तो हल 8/17 होता। यदि प्रश्न ![]() होता, तो हल 0 होता। प्रश्न के लिखे अनुसार हल निम्न है:)
होता, तो हल 0 होता। प्रश्न के लिखे अनुसार हल निम्न है:)
- हल:
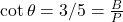 .
. 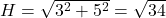 .
.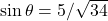 ,
, 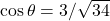 .
.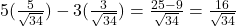 .
. - उत्तर:
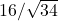
प्र.14 यदि ![]() हो तो
हो तो ![]() का मान क्या होगा?
का मान क्या होगा?
- हल:
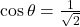 .
. - उत्तर:

प्र.15 ![]() का मान क्या होगा?
का मान क्या होगा?
- हल:
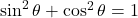 .
. - उत्तर: 1
प्र.16 यदि ![]() हो तो
हो तो ![]() का मान क्या होगा?
का मान क्या होगा?
- हल:
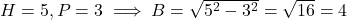 .
.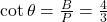 .
. - उत्तर:
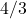
प्र.17 ![]() का मान क्या होगा?
का मान क्या होगा?
- हल:
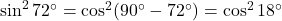 .
.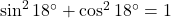 .
. - उत्तर: 1
प्र.18 यदि ![]() हो तो
हो तो ![]() से
से ![]() के बीच
के बीच ![]() का मान क्या होगा?
का मान क्या होगा?
- हल:
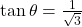 .
. - उत्तर:
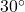
प्र.19 दिखाइए कि ![]() .
.
- हल: यह
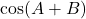 का सूत्र है।
का सूत्र है। 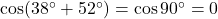 .
.
(इति सिद्धम)
प्र.20 यदि ![]() और
और ![]() त्रिभुज
त्रिभुज ![]() के अंतःकोण हों तो
के अंतःकोण हों तो ![]() .
.
- हल:
 .
.
LHS: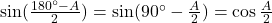 . (इति सिद्धम)
. (इति सिद्धम)
प्र.21 यदि ![]() … तो
… तो ![]() का मान ज्ञात कीजिए।
का मान ज्ञात कीजिए।
- हल:
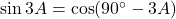 .
.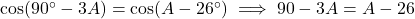
 .
. - उत्तर:
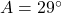
प्र.22 सिद्ध कीजिए: ![]() .
.
- हल: लंब (P), आधार (B), कर्ण (H) से,
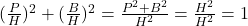 . (इति सिद्धम)
. (इति सिद्धम)
प्र.23 यदि ![]() तो जाँच कीजिए…
तो जाँच कीजिए…
(नोट: प्रश्न में ![]() त्रुटिपूर्ण है, क्योंकि
त्रुटिपूर्ण है, क्योंकि ![]() असंभव है। इसे
असंभव है। इसे ![]() मानते हुए हल किया गया है।)
मानते हुए हल किया गया है।)
- हल:
 .
. 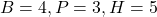 .
.
LHS: .
.
RHS: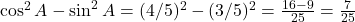 .
. - उत्तर: हाँ, है।
प्र.24 ![]() और
और ![]() … A और B का मान ज्ञात कीजिए।
… A और B का मान ज्ञात कीजिए।
- हल:
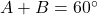 (1) और
(1) और 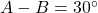 (2).
(2).
(1) + (2): .
.
(1) में रखने पर: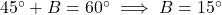 .
. - उत्तर:
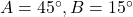
प्र.25 मान निकालिए: ![]() .
.
- हल:
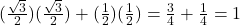 .
. - उत्तर: 1
प्र.26 मान निकालिए: ![]() .
.
- हल:
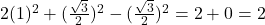 .
. - उत्तर: 2
प्र.27 दिखाइए कि: ![]() .
.
- हल:
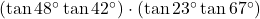
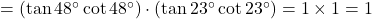 . (इति सिद्धम)
. (इति सिद्धम)
प्र.28 यदि ![]() … A का मान ज्ञात कीजिए।
… A का मान ज्ञात कीजिए।
- हल:
 .
.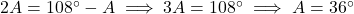 .
. - उत्तर:
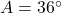
प्र.29 यदि ![]() … A का मान ज्ञात कीजिए।
… A का मान ज्ञात कीजिए।
- हल:
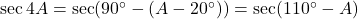 .
.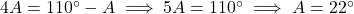 .
. - उत्तर:
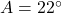
प्र.30 मान निकालिए: ![]() .
.
- हल:
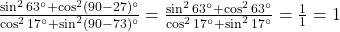 .
. - उत्तर: 1
प्र.31 मान निकालिए: ![]() .
.
- हल: (यह प्र.04(viii) का दोहराव है)
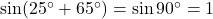 .
. - उत्तर: 1
प्र.32 यदि ![]() , हो तो
, हो तो ![]() के अन्य त्रिकोणमितीय अनुपात ज्ञात कीजिए।
के अन्य त्रिकोणमितीय अनुपात ज्ञात कीजिए।
- हल:
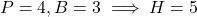 .
. - उत्तर:
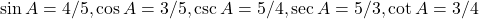
प्र.33 यदि ![]() , हो तो
, हो तो ![]() का मान ज्ञात कीजिए। (माना
का मान ज्ञात कीजिए। (माना ![]() )
)
- हल:
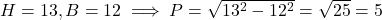 .
. - उत्तर:
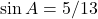
प्र.34 यदि ![]() , तो
, तो ![]() और
और ![]() का मान परिकलित कीजिए।
का मान परिकलित कीजिए।
- हल:
 .
. - उत्तर:
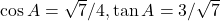
प्र.35 यदि ![]() हो तो
हो तो ![]() और
और ![]() का मान परिकलित कीजिए।
का मान परिकलित कीजिए।
- हल: (यह प्र.06 का दोहराव है)
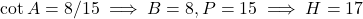 .
. - उत्तर:
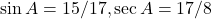
प्र.36 ![]() में जिसका कोण
में जिसका कोण ![]() समकोण है,
समकोण है, ![]() cm और
cm और ![]() cm है, तो
cm है, तो ![]() और
और ![]() के मान ज्ञात कीजिए।
के मान ज्ञात कीजिए।
- हल:
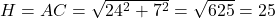 .
.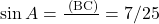 .
.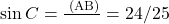 .
. - उत्तर:
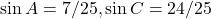
प्र.37 ![]() का मान परिकलित कीजिए।
का मान परिकलित कीजिए।
- हल: (यह प्र.04(vi) का दोहराव है)
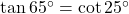 .
. - उत्तर: 1
प्र.38 ![]() का मान परिकलित कीजिए।
का मान परिकलित कीजिए।
- हल:
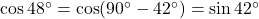 .
.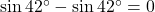 .
. - उत्तर: 0
प्र.39 यदि ![]() , तो सिद्ध कीजिए कि
, तो सिद्ध कीजिए कि ![]() .
.
- हल:
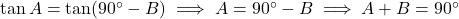 . (इति सिद्धम)
. (इति सिद्धम)
प्र.40 ![]() को
को ![]() और
और ![]() के बीच के कोणों में व्यक्त कीजिए।
के बीच के कोणों में व्यक्त कीजिए।
- हल:
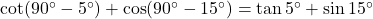 .
. - उत्तर:
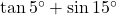
प्र.41 ![]() को
को ![]() और
और ![]() के बीच के कोणों में व्यक्त कीजिए।
के बीच के कोणों में व्यक्त कीजिए।
- हल:
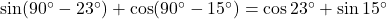 .
. - उत्तर:
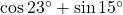
प्र.42 सिद्ध कीजिए: ![]()
- हल: LHS =
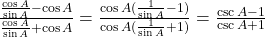 . (इति सिद्धम)
. (इति सिद्धम)
प्र.43 सिद्ध कीजिए: ![]()
- हल: LHS =
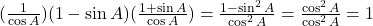 . (इति सिद्धम)
. (इति सिद्धम)
प्र.44 सिद्ध कीजिए: ![]() .
.
- हल: LHS =
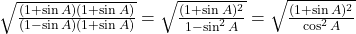
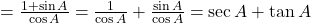 . (इति सिद्धम)
. (इति सिद्धम)
प्र.45 सिद्ध कीजिए: ![]()
- हल: LHS =
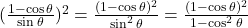
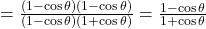 . (इति सिद्धम)
. (इति सिद्धम)
प्र.46 सिद्ध कीजिए: ![]()
- हल: LHS =
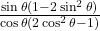 . चूँकि
. चूँकि 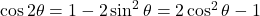 .
.
LHS =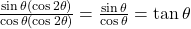 . (इति सिद्धम)
. (इति सिद्धम)
प्र.47 ![]() सिद्ध कीजिए।
सिद्ध कीजिए।
- हल: अंश और हर को
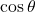 से भाग देने पर:
से भाग देने पर:
LHS =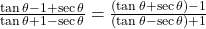
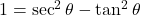 को अंश में रखने पर:
को अंश में रखने पर: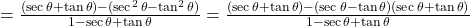
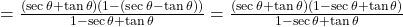
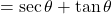 .
.
RHS =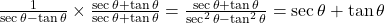 . (इति सिद्धम)
. (इति सिद्धम)
प्र.48 ![]() को सिद्ध कीजिए।
को सिद्ध कीजिए।
- हल:
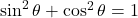 को
को  से भाग देने पर:
से भाग देने पर: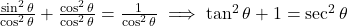 . (इति सिद्धम)
. (इति सिद्धम)
प्र.49 ![]() तो
तो ![]() का मान ज्ञात कीजिए।
का मान ज्ञात कीजिए।
- हल:
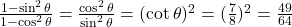 .
. - उत्तर: 49/64
प्र.50 ![]() में
में ![]() समकोण है,
समकोण है, ![]() cm और
cm और ![]() cm है।
cm है। ![]() और
और ![]() के मान ज्ञात कीजिए।
के मान ज्ञात कीजिए।
- हल:
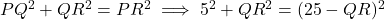
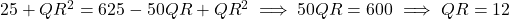 cm.
cm. cm.
cm.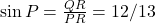 ,
,  ,
, 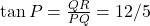 .
. - उत्तर:
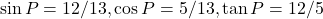
प्र.51 सिद्ध कीजिए: ![]() .
.
- हल: LHS =
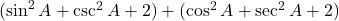
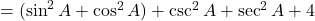
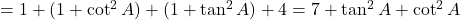 . (इति सिद्धम)
. (इति सिद्धम)
प्र.52 सिद्ध कीजिए: ![]() .
.
- हल: LHS =
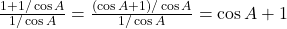 .
.
RHS =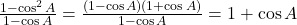 . (इति सिद्धम)
. (इति सिद्धम)
प्र.53 यदि ![]() और
और ![]() न्यूनकोण हों जिससे कि
न्यूनकोण हों जिससे कि ![]() , तो सिद्ध कीजिए कि
, तो सिद्ध कीजिए कि ![]() .
.
- हल: चूँकि
 से
से  (न्यूनकोण) के बीच
(न्यूनकोण) के बीच 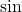 फलन एक-से-एक (one-to-one) होता है, यदि
फलन एक-से-एक (one-to-one) होता है, यदि 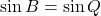 है, तो
है, तो 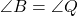 होना अनिवार्य है। (इति सिद्धम)
होना अनिवार्य है। (इति सिद्धम)
प्र.54 समकोण ![]() में
में ![]() समकोण है, यदि
समकोण है, यदि ![]() तो सत्यापित कीजिए कि
तो सत्यापित कीजिए कि ![]() .
.
- हल:
 .
.
LHS =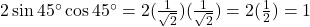 . (इति सिद्धम)
. (इति सिद्धम)
प्र.55 ![]() का मान ज्ञात कीजिए।
का मान ज्ञात कीजिए।
- हल:
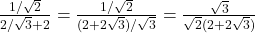
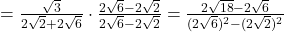
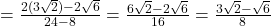 .
. - उत्तर: