MP Board 10th Triangle Question Bank : अध्याय-6: त्रिभुज प्रश्न बैंक
अध्याय 6: त्रिभुज MP Board 10th Triangle Question Bank
स्मरणीय बिंदु
- वे सभी आकृतियाँ जिनके आकार (Shapes) समान होते हैं परन्तु इनके माप (Sizes) समान होने आवश्यक नहीं हैं, समरूप आकृतियाँ कहलाती हैं। सभी वृत्त समरूप होते हैं।
- दो बहुभुज (Polygons) समरूप कहलाते हैं यदि उनके संगत कोण बराबर हों और उनकी संगत भुजाएँ समानुपातिक हों।
- चतुर्भुज ABCD और चतुर्भुज PQRS में
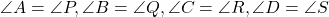 तथा
तथा 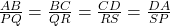
अतः चतुर्भुज ABCD ~ चतुर्भुज PQRS - सभी वृत्त समरूप होते हैं।
- सभी वर्ग समरूप होते हैं।
- सभी समबाहु त्रिभुज समरूप होते हैं।
- दो त्रिभुज समरूप होते हैं यदि उनके संगत कोण बराबर हों और उनकी संगत भुजाएँ समानुपातिक हों।
 और
और 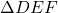 में यदि
में यदि 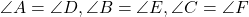 तथा
तथा 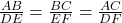
तो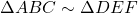
- दो समानकोणिक त्रिभुजों में उनकी संगत भुजाओं का अनुपात सदैव समान रहता है।
- आधारभूत आनुपातिकता प्रमेय (Basic Proportionality Theorem) (थेल्स प्रमेय (Thales Theorem)) : यदि किसी त्रिभुज की एक भुजा के समान्तर अन्य दो भुजाओं को भिन्न-भिन्न बिन्दुओं पर प्रतिच्छेद करने के लिए एक रेखा खींची जाए, तो ये अन्य दो भुजाएँ एक ही अनुपात में विभाजित हो जाती हैं।
 में यदि
में यदि  तो
तो 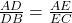
- आधारभूत आनुपातिकता प्रमेय का विलोम (Converse Basic Proportionality Theorem): यदि एक रेखा किसी त्रिभुज की दो भुजाओं को एक ही अनुपात में विभाजित करे, तो वह तीसरी भुजा के समान्तर होती है।
 में यदि
में यदि 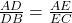 तो
तो 
- त्रिभुजों की समरूपता के लिए कसौटियाँ (Criteria for Similarity of Triangles)
- AAA (कोण – कोण – कोण) कसौटी: यदि दो त्रिभुजों में, संगत कोण बराबर हों, तो उनकी संगत भुजाएँ एक ही अनुपात में (समानुपाती) होती हैं और इसीलिए ये त्रिभुज समरूप होते हैं।
- AA (कोण – कोण ) कसौटी: यदि एक त्रिभुज के दो कोण एक अन्य त्रिभुज के क्रमशः दो कोणों के बराबर हों, तो दोनों त्रिभुज समरूप होते हैं।
- SSS (भुजा – भुजा – भुजा) कसौटी: यदि दो त्रिभुजों में, एक त्रिभुज की भुजाएँ दूसरे त्रिभुज की भुजाओं के समानुपाती हों तो इनके संगत कोण बराबर होते हैं, और इसीलिए ये त्रिभुज समरूप होते हैं।
- SAS (भुजा – कोण – भुजा): यदि एक त्रिभुज का एक कोण दुसरे त्रिभुज के एक कोण के बराबर हो तथा इन कोणों को अंतर्गत करने वाली भुजाएँ समानुपाती हों, तो दोनों त्रिभुज समरूप होते हैं।
- दो समरूप त्रिभुजों के क्षेत्रफलों का अनुपात इनकी संगत भुजाओं के अनुपात के वर्ग के बराबर होता है।
- दो समरूप त्रिभुजों की भुजाएँ 4:9 के अनुपात में हैं। इन त्रिभुजों के क्षेत्रफलों का अनुपात 16:81 होगा।
- यदि किसी समकोण त्रिभुज के समकोण वाले शीर्ष से कर्ण पर लंब डाला जाए तो इस लंब के दोनों ओर बने त्रिभुज संपूर्ण त्रिभुज के समरूप होते हैं तथा परस्पर भी समरूप होते हैं।
- पाइथागोरस प्रमेय: एक समकोण त्रिभुज में कर्ण का वर्ग शेष दो भुजाओं के वर्गों के योग के बराबर होता है।
- पाइथागोरस प्रमेय को पहले एक प्राचीन भारतीय गणितज्ञ बौधायन (लगभग 800 ई. पू.) ने निम्नलिखित रूप में दिया था:
एक आयत का विकर्ण स्वयं से उतना ही क्षेत्रफल निर्मित करता है, जितना उसकी दोनों भुजाओं से मिलकर बनता है।
इसका अर्थ है; किसी आयत के विकर्ण से बने वर्ग का क्षेत्रफल इसकी दोनों आसन्न भुजाओं पर बने वर्गों के योग के बराबर होता है।
इस कारण पाइथागोरस प्रमेय को कभी-कभी बौधायन प्रमेय भी कहा जाता है। - पाइथागोरस प्रमेय का विलोम (Converse of Pythagoras Theorem): यदि किसी त्रिभुज की एक भुजा का वर्ग अन्य दो भुजाओं के वर्गों के योग के बराबर हो तो पहली भुजा का सम्मुख कोण समकोण होता है।
यहाँ सभी छवियों में दिए गए प्रश्नों के हल क्रमबद्ध तरीके से दिए गए हैं:
प्र.1 सही विकल्प चुनिए
- यदि किसी त्रिभुज की एक भुजा के समान्तर अन्य दो भुजाओं को भिन्न-भिन्न बिन्दुओं पर प्रतिच्छेद करने के लिए एक रेखा खींची जाए, तो ये अन्य दो भुजाएँ एक ही अनुपात में विभाजित हो जाती हैं। इस कथन को … नाम से जाना जाता है:
- हल: यह आधारभूत आनुपातिकता प्रमेय या थेल्स प्रमेय का कथन है।
- सही विकल्प: (A) आधारभूत आनुपातिकता प्रमेय
 में,
में, 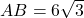 cm,
cm, 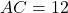 cm और
cm और 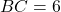 cm है। तब
cm है। तब 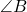 का मान होगा:
का मान होगा:
- हल: हम पाइथागोरस प्रमेय के विलोम की जाँच करेंगे।
- सबसे बड़ी भुजा
 है:
है: 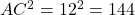
- अन्य दो भुजाएँ:
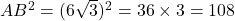
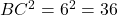
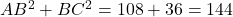
- सबसे बड़ी भुजा
- चूँकि
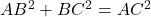 है, यह एक समकोण त्रिभुज है, जिसमें
है, यह एक समकोण त्रिभुज है, जिसमें  कर्ण है। कर्ण के सामने का कोण (
कर्ण है। कर्ण के सामने का कोण (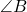 ) समकोण होगा।
) समकोण होगा। - सही विकल्प: (C)

- हल: हम पाइथागोरस प्रमेय के विलोम की जाँच करेंगे।
- किसी
 में
में  तथा
तथा 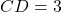 cm,
cm, 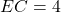 cm,
cm, 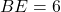 cm तब
cm तब  होगा:
होगा:
- हल: (यहाँ
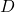 भुजा
भुजा  पर और
पर और 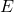 भुजा
भुजा  पर है)। थेल्स प्रमेय (BPT) के उप-प्रमेय से, यदि
पर है)। थेल्स प्रमेय (BPT) के उप-प्रमेय से, यदि  है, तो
है, तो 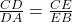 .
.
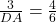
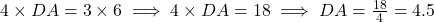 cm.
cm.
- सही विकल्प: (C) 4.5 cm
- हल: (यहाँ
- यदि एक त्रिभुज में किसी भुजा का वर्ग, अन्य दो भुजाओं के वर्गों के योग के बराबर हो तो पहली भुजा का सम्मुख कोण होगा:
- हल: यह पाइथागोरस प्रमेय का विलोम है। कोण समकोण (
 ) होता है।
) होता है। - सही विकल्प: (A)

- हल: यह पाइथागोरस प्रमेय का विलोम है। कोण समकोण (
- किसी त्रिभुज
 में
में  है।
है। 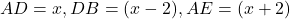 तथा
तथा  तब
तब  का मान होगा:
का मान होगा:
- हल: थेल्स प्रमेय (BPT) से:
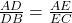
- सही विकल्प: (B) 4
- हल: थेल्स प्रमेय (BPT) से:
- दो समरूप त्रिभुजों के भुजाओं का अनुपात
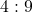 है तो त्रिभुजों के क्षेत्रफलों का अनुपात क्या होगा।
है तो त्रिभुजों के क्षेत्रफलों का अनुपात क्या होगा।
- हल: क्षेत्रफलों का अनुपात =
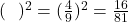
- सही विकल्प: (D)
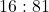 (नोट: विकल्प C
(नोट: विकल्प C 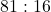 है)
है)
- हल: क्षेत्रफलों का अनुपात =
- पाइथागोरस प्रमेय भारत में निम्न गणितज्ञ द्वारा दिया गया था
- हल: बौधायन (बौधायन प्रमेय)।
- सही विकल्प: (D) बौधायन
- सभी वर्ग होते हैं:
- हल: सभी वर्गों के संगत कोण बराबर (
 ) और संगत भुजाएँ समानुपाती होती हैं, इसलिए वे समरूप होते हैं।
) और संगत भुजाएँ समानुपाती होती हैं, इसलिए वे समरूप होते हैं। - सही विकल्प: (B) समरूप
- हल: सभी वर्गों के संगत कोण बराबर (
- एक आदमी पूर्व की ओर 12 मी चलता है और फिर वह उत्तर की ओर 9 मीटर चलता है। अब वह प्रारंभिक बिंदु से कितनी दूर होगा
- हल: यह एक समकोण त्रिभुज बनाता है। दूरी (कर्ण) =
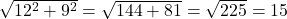 मी।
मी। - सही विकल्प: (C) 15 मी
- हल: यह एक समकोण त्रिभुज बनाता है। दूरी (कर्ण) =
- निम्न में से कौन-सा समकोण त्रिभुज है यदि भुजाओं की लम्बाई निम्न है:
- हल: हम पाइथागोरस ट्रिपलेट की जाँच करेंगे (
 )
)
- (A)
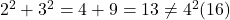
- (B)
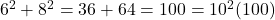
- (A)
- सही विकल्प: (B) 6, 8, 10
- हल: हम पाइथागोरस ट्रिपलेट की जाँच करेंगे (
- दो समरूप त्रिभुजों के क्षेत्रफल क्रमशः
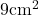 और
और 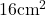 हैं, तो उनकी भुजाओं का अनुपात है:
हैं, तो उनकी भुजाओं का अनुपात है:
- हल: भुजाओं का अनुपात =
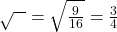
- सही विकल्प: (A)
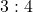
- हल: भुजाओं का अनुपात =
 एक समद्विबाहु समकोण त्रिभुज है, जहाँ
एक समद्विबाहु समकोण त्रिभुज है, जहाँ 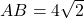 cm और
cm और 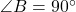 है, तो उनके कर्ण की लम्बाई
है, तो उनके कर्ण की लम्बाई
- हल: चूँकि त्रिभुज समद्विबाहु है और
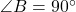 है, तो
है, तो 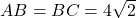 .
. - कर्ण
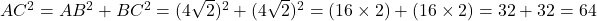
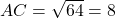 cm.
cm.- सही विकल्प: (B) 8 cm
- हल: चूँकि त्रिभुज समद्विबाहु है और
- किसी समबाहु त्रिभुज में यदि
 तो
तो
- हल: माना समबाहु त्रिभुज की भुजा
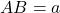 .
.  लम्ब है, इसलिए
लम्ब है, इसलिए 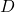 मध्य बिंदु होगा,
मध्य बिंदु होगा, 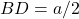 .
. 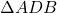 में,
में, 
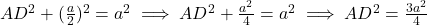
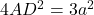 .
.  को
को 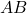 से बदलने पर:
से बदलने पर: 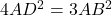 .
.- सही विकल्प: (C)
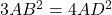
- हल: माना समबाहु त्रिभुज की भुजा
- समरूपता के लिये आवश्यक प्रतिवंध है:
- हल: (A) कोण-कोण-कोण (AAA) और (B) कोण-कोण (AA) दोनों समरूपता की कसौटियाँ हैं। (C) ‘कोण-भुजा-कोण’ सर्वांगसमता की कसौटी है, समरूपता की नहीं (संभवतः यह भुजा-कोण-भुजा (SAS) के लिए एक टाइपो है)। यदि (A) और (B) दोनों सही हैं, तो सबसे उपयुक्त उत्तर (D) होगा।
- सही विकल्प: (D) उपर्युक्त सभी
- भुजाओं 8 cm, 15 cm, 17 cm, से निर्मित त्रिभुज होगा:
- हल:
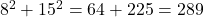 .
.  .
. - चूँकि
 , यह एक समकोण त्रिभुज है।
, यह एक समकोण त्रिभुज है। - सही विकल्प: (B) समकोण त्रिभुज
- हल:
प्र.2 रिक्त स्थान की पूर्ति कीजिए
- सभी वृत्त समरूप होते हैं। (सर्वांगसम केवल तब होते हैं जब त्रिज्या बराबर हो)
- सभी वर्ग समरूप होते हैं।
- सभी समबाहु त्रिभुज समरूप होते हैं।
- दो समान कोणिक त्रिभुजों में उनकी संगत भुजाओं का अनुपात सदैव समान होता है।
- यदि एक रेखा किसी त्रिभुज की दो भुजाओं को एक ही अनुपात में विभाजित करे, तो वह तीसरी भुजा के समान्तर होती है। (थेल्स प्रमेय का विलोम)
- समरूप त्रिभुज की संगत भुजाएँ समानुपाती होती हैं।
- समरूप त्रिभुज के संगत कोण बराबर होते हैं।
- दो समरूप त्रिभुजों के क्षेत्रफलों का अनुपात किन्हीं दो भुजाओं के वर्ग के अनुपात के बराबर होता है।
- यदि दो त्रिभुजों की संगत भुजाएँ समानुपातिक हों, तो त्रिभुज समरूप होंगें। (SSS समरूपता)
- दो समरूप त्रिभुजों के क्षेत्रफलों में
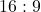 का अनुपात है। तो उनकी संगत भुजाओं में
का अनुपात है। तो उनकी संगत भुजाओं में  का अनुपात होगा।
का अनुपात होगा। - दो समरूप त्रिभुजों की भुजाओं का अनुपात
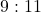 है। तो उनके क्षेत्रफलों का अनुपात
है। तो उनके क्षेत्रफलों का अनुपात 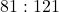 होगा।
होगा।
प्र.3 सही जोड़ी मिलाइए
| स्तम्भ- अ | स्तम्भ- ब |
|---|---|
| I. त्रिभुज समरूप होते हैं | (d) समबाहु (सभी समबाहु त्रिभुज समरूप होते हैं) |
| II. आधारभूत आनुपातिक प्रमेय | (a) थेल्स प्रमेय |
| III. सभी वर्ग होते हैं | (b) समरूप |
| IV. पाइथागोरस प्रमेय | (c) |
| V. त्रिभुजों की माध्यिकाएँ | (f) संगामी (माध्यिकाएँ केंद्रक पर संगामी होती हैं) |
| VI. समरूप त्रिभुजों की संगत भुजाएँ | (e) अनुपातिक (या समानुपातिक) |
प्र.4 एक शब्द / वाक्य में उत्तर दीजिए
- क्या सभी समद्विबाहु त्रिभुज समरूप होते हैं?
उत्तर: नहीं। - क्या सभी वर्ग समरूप होते हैं?
उत्तर: हाँ। - थेल्स प्रमेय का कथन लिखिए।
उत्तर: यदि किसी त्रिभुज की एक भुजा के समान्तर अन्य दो भुजाओं को भिन्न-भिन्न बिन्दुओं पर प्रतिच्छेद करने के लिए एक रेखा खींची जाए, तो ये अन्य दो भुजाएँ एक ही अनुपात में विभाजित हो जाती हैं। - पाइथागोरस प्रमेय का कथन क्या है?
उत्तर: एक समकोण त्रिभुज में, कर्ण का वर्ग शेष दो भुजाओं के वर्गों के योग के बराबर होता है। - क्या भुजाओं 6cm, 8cm एवं 10cm से निर्मित त्रिभुज समकोण त्रिभुज होगा?
उत्तर: हाँ (क्योंकि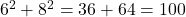 , जो
, जो 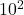 के बराबर है)।
के बराबर है)। - एक आदमी 10 m पूर्व की ओर और उसके पश्चात् 24 m उत्तर की ओर जाता है तो उसकी प्रारंभिक बिंदु से दूरी क्या होगी?
उत्तर: दूरी =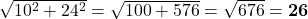 मी।
मी। - यदि कोई दो समरूप त्रिभुजों की माध्यिकाओं का अनुपात
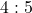 है तो उनके क्षेत्रफलों का अनुपात होगा।
है तो उनके क्षेत्रफलों का अनुपात होगा।
उत्तर: क्षेत्रफलों का अनुपात =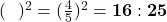 .
. - समकोण त्रिभुज की सबसे बड़ी भुजा को कहते हैं?
उत्तर: कर्ण।
ज़रूर, यहाँ सभी प्रश्नों को उनके हलों के साथ व्यवस्थित रूप से प्रस्तुत किया गया है।
प्र.1 सही विकल्प चुनिए
1. यदि किसी त्रिभुज की एक भुजा के समान्तर अन्य दो भुजाओं को भिन्न-भिन्न बिन्दुओं पर प्रतिच्छेद करने के लिए एक रेखा खींची जाए, तो ये अन्य दो भुजाएँ एक ही अनुपात में विभाजित हो जाती हैं। इस कथन को निम्नलिखित नाम से जाना जाता है:
(A) आधारभूत आनुपातिकता प्रमेय
(B) पाइथागोरस प्रमेय
(C) RHS प्रमेय
(D) इनमें से कोई नहीं
- हल: यह आधारभूत आनुपातिकता प्रमेय (थेल्स प्रमेय) का कथन है।
- सही विकल्प: (A) आधारभूत आनुपातिकता प्रमेय
2. ![]() में,
में, ![]() cm,
cm, ![]() cm और
cm और ![]() cm है। तब
cm है। तब ![]() का मान होगा:
का मान होगा:
(A) ![]()
(B) ![]()
(C) ![]()
(D) ![]()
- हल: पाइथागोरस प्रमेय के विलोम की जाँच करने पर:
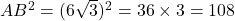
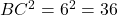
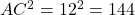
- चूँकि
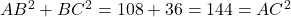 है, यह एक समकोण त्रिभुज है।
है, यह एक समकोण त्रिभुज है।  कर्ण है, अतः उसके सामने का कोण (
कर्ण है, अतः उसके सामने का कोण (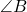 ) समकोण होगा।
) समकोण होगा।
- सही विकल्प: (C)

3. किसी ![]() में
में ![]() तथा
तथा ![]() cm,
cm, ![]() cm,
cm, ![]() cm तब
cm तब ![]() होगा:
होगा:
(A) 7.5 cm
(B) 3 cm
(C) 4.5 cm
(D) 6 cm
- हल: थेल्स प्रमेय (BPT) के उप-प्रमेय से, यदि
 है, तो
है, तो 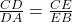 .
.
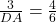
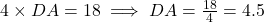 cm.
cm.
- सही विकल्प: (C) 4.5 cm
4. यदि एक त्रिभुज में किसी भुजा का वर्ग, अन्य दो भुजाओं के वर्गों के योग के बराबर हो तो पहली भुजा का सम्मुख कोण होगा:
(A) ![]()
(B) ![]()
(C) ![]()
(D) ![]()
- हल: यह पाइथागोरस प्रमेय के विलोम का कथन है।
- सही विकल्प: (A)

5. किसी त्रिभुज ![]() में
में ![]() है।
है। ![]() तथा
तथा ![]() तब
तब ![]() का मान होगा:
का मान होगा:
(A) 5
(B) 4
(C) 3
(D) 2
- हल: थेल्स प्रमेय से:
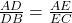
- सही विकल्प: (B) 4
6. दो समरूप त्रिभुजों के भुजाओं का अनुपात ![]() है तो त्रिभुजों के क्षेत्रफलों का अनुपात क्या होगा।
है तो त्रिभुजों के क्षेत्रफलों का अनुपात क्या होगा।
(A) 2 : 3
(B) 4 : 9
(C) 81 : 16
(D) 16 : 81
- हल: क्षेत्रफलों का अनुपात =
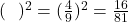
- सही विकल्प: (D) 16 : 81
7. पाइथागोरस प्रमेय भारत में निम्न गणितज्ञ द्वारा दिया गया था
(A) आर्यभट्ट
(B) श्रीधराचार्य
(C) ब्रह्मगुप्त
(D) बौधायन
- सही विकल्प: (D) बौधायन
8. सभी वर्ग होते हैं:
(A) समान
(B) समरूप
(C) सर्वांगसम
(D) उपर्युक्त सभी
- हल: सभी वर्गों के कोण बराबर (
 ) और भुजाएँ आनुपातिक होती हैं।
) और भुजाएँ आनुपातिक होती हैं। - सही विकल्प: (B) समरूप
9. एक आदमी पूर्व की ओर 12 मी चलता है और फिर वह उत्तर की ओर 9 मीटर चलता है। अब वह प्रारंभिक बिंदु से कितनी दूर होगा
(A) 12 मी
(B) 9 मी
(C) 15 मी
(D) 25 मी
- हल: पाइथागोरस प्रमेय से:
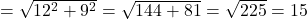 मी।
मी। - सही विकल्प: (C) 15 मी
10. निम्न में से कौन-सा समकोण त्रिभुज है…
(A) 2, 3, 4
(B) 6, 8, 10
(C) 8, 5, 11
(D) 8, 15, 19
- हल:
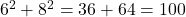 , जो
, जो 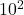 के बराबर है।
के बराबर है। - सही विकल्प: (B) 6, 8, 10
11. दो समरूप त्रिभुजों के क्षेत्रफल क्रमशः ![]() और
और ![]() हैं, तो उनकी भुजाओं का अनुपात है:
हैं, तो उनकी भुजाओं का अनुपात है:
(A) 3 : 4
(B) 4 : 7
(C) 2 : 3
(D) 4 : 5
- हल: भुजाओं का अनुपात =
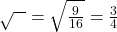
- सही विकल्प: (A) 3 : 4
12. ![]() एक समद्विबाहु समकोण त्रिभुज है, जहाँ
एक समद्विबाहु समकोण त्रिभुज है, जहाँ ![]() cm और
cm और ![]() है, तो उनके कर्ण की लम्बाई
है, तो उनके कर्ण की लम्बाई
(A) 12 cm
(B) 8 cm
(C) ![]() cm
cm
(D) ![]() cm
cm
- हल: समद्विबाहु होने के कारण
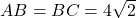 .
.
- कर्ण
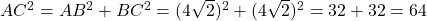
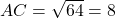 cm.
cm.
- कर्ण
- सही विकल्प: (B) 8 cm
13. किसी समबाहु त्रिभुज में यदि ![]() तो
तो
(A) ![]()
(B) ![]()
(C) ![]()
(D) ![]()
- हल:
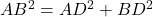 . चूँकि
. चूँकि 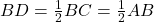 ,
,
- सही विकल्प: (C)
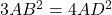
14. समरूपता के लिये आवश्यक प्रतिवंध है:
(A) कोण-कोण-कोण समरूपता
(B) कोण-कोण समरूपता
(C) कोण-भुजा-कोण समरूपता
(D) उपर्युक्त सभी
- हल: (A), (B), (SSS), और (SAS) समरूपता की कसौटियाँ हैं। (C) सर्वांगसमता की कसौटी है। दिए गए विकल्पों में (A) और (B) दोनों सही हैं, इसलिए (D) सबसे उपयुक्त है।
- सही विकल्प: (D) उपर्युक्त सभी
15. भुजाओं 8 cm, 15 cm, 17 cm, से निर्मित त्रिभुज होगा:
(A) समद्विबाहु त्रिभुज
(B) समकोण त्रिभुज
(C) समद्विबाहु समकोण
(D) समबाहु त्रिभुज
- हल:
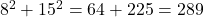 , जो
, जो 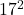 के बराबर है।
के बराबर है। - सही विकल्प: (B) समकोण त्रिभुज
प्र.2 रिक्त स्थान की पूर्ति कीजिए
- सभी वृत्त समरूप होते हैं।
- सभी वर्ग समरूप होते हैं।
- सभी समबाहु त्रिभुज समरूप होते हैं।
- दो समान कोणिक त्रिभुजों में उनकी संगत भुजाओं का अनुपात सदैव समान होता है।
- यदि एक रेखा किसी त्रिभुज की दो भुजाओं को एक ही अनुपात में विभाजित करे, तो वह तीसरी भुजा के समान्तर होती है।
- समरूप त्रिभुज की संगत भुजाएँ समानुपाती होती हैं।
- समरूप त्रिभुज के संगत कोण बराबर होते हैं।
- दो समरूप त्रिभुजों के क्षेत्रफलों का अनुपात किन्हीं दो भुजाओं के वर्ग के अनुपात के बराबर होता है।
- यदि दो त्रिभुजों की संगत भुजाएँ समानुपातिक हों, तो त्रिभुज समरूप होंगें।
- दो समरूप त्रिभुजों के क्षेत्रफलों में
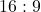 का अनुपात है। तो उनकी संगत भुजाओं में 4 : 3 का अनुपात होगा।
का अनुपात है। तो उनकी संगत भुजाओं में 4 : 3 का अनुपात होगा। - दो समरूप त्रिभुजों की भुजाओं का अनुपात
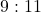 है। तो उनके क्षेत्रफलों का अनुपात 81 : 121 होगा।
है। तो उनके क्षेत्रफलों का अनुपात 81 : 121 होगा।
प्र.3 सही जोड़ी मिलाइए
| स्तम्भ- अ | स्तम्भ- ब | सही जोड़ी |
|---|---|---|
| I. त्रिभुज समरूप होते हैं | (a) थेल्स प्रमेय | (d) समबाहु |
| II. आधारभूत आनुपातिक प्रमेय | (b) समरूप | (a) थेल्स प्रमेय |
| III. सभी वर्ग होते हैं | (c) | (b) समरूप |
| IV. पाइथागोरस प्रमेय | (d) समबाहु | (c) |
| V. त्रिभुजों की माध्यिकाएँ | (e) अनुपातिक | (f) संगामी |
| VI. समरूप त्रिभुजों की संगत भुजाएँ | (f) संगामी | (e) अनुपातिक |
प्र.4 एक शब्द / वाक्य में उत्तर दीजिए
1. क्या सभी समद्विबाहु त्रिभुज समरूप होते हैं?
उत्तर: नहीं।
2. क्या सभी वर्ग समरूप होते हैं?
उत्तर: हाँ।
3. थेल्स प्रमेय का कथन लिखिए।
उत्तर: यदि किसी त्रिभुज की एक भुजा के समान्तर अन्य दो भुजाओं को भिन्न-भिन्न बिन्दुओं पर प्रतिच्छेद करने के लिए एक रेखा खींची जाए, तो ये अन्य दो भुजाएँ एक ही अनुपात में विभाजित हो जाती हैं।
4. पाइथागोरस प्रमेय का कथन क्या है?
उत्तर: एक समकोण त्रिभुज में, कर्ण का वर्ग शेष दो भुजाओं के वर्गों के योग के बराबर होता है।
5. क्या भुजाओं 6cm, 8cm एवं 10cm से निर्मित त्रिभुज समकोण त्रिभुज होगा?
उत्तर: हाँ, क्योंकि ![]() (36 + 64 = 100)।
(36 + 64 = 100)।
6. एक आदमी 10 m पूर्व की ओर और उसके पश्चात् 24 m उत्तर की ओर जाता है तो उसकी प्रारंभिक बिंदु से दूरी क्या होगी?
उत्तर: ![]() मी।
मी।
7. यदि कोई दो समरूप त्रिभुजों की माध्यिकाओं का अनुपात ![]() है तो उनके क्षेत्रफलों का अनुपात होगा।
है तो उनके क्षेत्रफलों का अनुपात होगा।
उत्तर: ![]() .
.
8. समकोण त्रिभुज की सबसे बड़ी भुजा को कहते हैं?
उत्तर: कर्ण।
प्र.5 सत्य / असत्य लिखिए
- दो त्रिभुजों में संगत कोण बराबर हों, तो उनकी संगत भुजाएँ एक ही अनुपात में (समानुपाती) होती हैं और इसीलिए ये त्रिभुज समरूप होते हैं। (सत्य)
- यदि एक त्रिभुज के दो कोण एक अन्य त्रिभुज के क्रमशः दो कोणों के बराबर हों, तो त्रिभुज समरूप होते हैं। (सत्य)
- एक समकोण त्रिभुज में कर्ण का वर्ग शेष दो भुजाओं के वर्गों के अंतर के बराबर होता है। (असत्य) (यह योग के बराबर होता है।)
- यदि किसी त्रिभुज की एक भुजा का वर्ग अन्य दो भुजाओं के वर्गों के योग के बराबर हो तो पहली भुजा का सम्मुख कोण समकोण होता है। (सत्य)
- यदि दो त्रिभुज समकोणिक हों तो त्रिभुज समरूप होंगे। (सत्य)
- यदि त्रिभुजों की संगत भुजाएँ आनुपातिक हों तो वे त्रिभुज समरूप नहीं होंगें। (असत्य) (वे SSS समरूपता से समरूप होते हैं।)
- समकोण त्रिभुज में कर्ण सबसे बड़ी भुजा होती है। (सत्य)
- समकोण त्रिभुज में कर्ण का वर्ग त्रिभुज की किसी एक भुजा के वर्ग के बराबर होता है। (असत्य)
- दो त्रिभुजों में संगत भुजाएँ एक ही अनुपात में हों, तो उनके संगत कोण बराबर होते हैं। (सत्य)
- त्रिभुज का क्षेत्रफल =
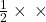 होती है। (सत्य)
होती है। (सत्य) - दो समरूप आकृतियाँ अनिवार्यतः सर्वांगसम होते है। (असत्य)
- दो सर्वांगसम त्रिभुज की आकृतिया सदैव समरूप होती है। (सत्य)
- दो समरूप त्रिभुजों के कोण आनुपातिक होते है। (असत्य) (कोण बराबर होते हैं।)
- दो समरूप त्रिभुजों के परिमाप आपस में बराबर होते है। (असत्य) (परिमाप आनुपातिक होते हैं।)
प्र.8 से प्र.41 (विश्लेषणात्मक प्रश्न)
प्र.8 6 मी. वाले ऊर्ध्वाधर स्तंभ की छाया 4 मी है, जबकि उसी समय एक मीनार की छाया 28 मी है। मीनार की ऊँचाई ज्ञात कीजिए।
- हल:

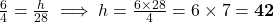 मी.
मी.
प्र.9 ![]() है, और उनके क्षेत्रफल 64 सेमी² और 121 सेमी² हैं। यदि
है, और उनके क्षेत्रफल 64 सेमी² और 121 सेमी² हैं। यदि ![]() cm हो तो
cm हो तो ![]() ज्ञात कीजिए।
ज्ञात कीजिए।
- हल:
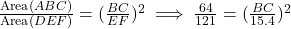
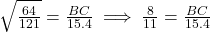
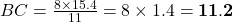 सेमी.
सेमी.
प्र.10 एक सीढ़ी दीवार पर इस प्रकार टिकी है कि निचला सिरा दीवार से 2.5 m की दूरी पर है तथा ऊपरी सिरा भूमि से 6 m की ऊँचाई पर बनी खिड़की तक पहुँचता है। सीढ़ी की लंबाई ज्ञात कीजिए।
- हल:
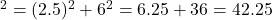
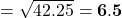 मी.
मी.
प्र.11 दो खंभे जिनकी ऊँचाई 6 मी और 11 मी है, समतल भूमि पर खड़े हैं। यदि पाद बिन्दुओं के बीच की दूरी 12 मी है तो ऊपरी सिरों के बीच की दूरी ज्ञात कीजिए।
- हल: यह एक समकोण त्रिभुज बनाता है जिसका आधार = 12 मी और लंब (ऊँचाई का अंतर) =
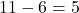 मी।
मी।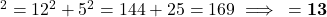 मी.
मी.
प्र.12 10 मी लंबी सीढ़ी दीवार पर टिकाने पर भूमि से 8 मी की ऊँचाई पर स्थित खिड़की तक पहुँचती है। दीवार के आधार से सीढ़ी के निचले सिरे की दूरी ज्ञात कीजिए।
- हल:
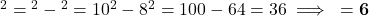 मी.
मी.
प्र.13 एक समबाहु त्रिभुज ABC की भुजा 2a है। उसके प्रत्येक शीर्षलंब की लंबाई ज्ञात कीजिए।
- हल:
 खींचने पर,
खींचने पर, 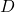 ,
,  का मध्य बिंदु होगा।
का मध्य बिंदु होगा। 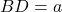 .
.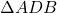 में,
में, 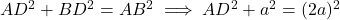
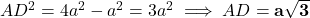
प्र.14 ![]() में,
में, ![]() और
और ![]() क्रमशः
क्रमशः ![]() और
और ![]() के बिंदु इस प्रकार
के बिंदु इस प्रकार ![]() हैं। यदि
हैं। यदि ![]() और
और ![]() तो
तो ![]() का मान ज्ञात कीजिए।
का मान ज्ञात कीजिए।
- हल:
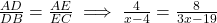
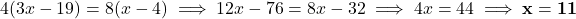
प्र.15 18 मी ऊँचे ऊर्ध्वाधर खंभे के ऊपरी सिरे से तार का एक सिरा जुड़ा है तथा तार का दूसरा सिरा खूँटे से जुड़ा है। खंभे के आधार से खूँटे को कितनी दूरी पर गाड़ा जाये कि तार तना रहे जबकि तार की लंबाई 24 मी है।
- हल:
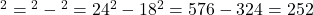
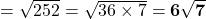 मी.
मी.
प्र.16 दो समरूप त्रिभुजों की परिमाप 25 सेमी और 15 सेमी है। यदि पहले त्रिभुज की एक भुजा 9 सेमी है तो दूसरे त्रिभुज की संगत भुजा की लंबाई ज्ञात कीजिए।
- हल:
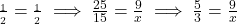
 सेमी.
सेमी.
प्र.17 दो समरूप त्रिभुजों के क्षेत्रफल 144 सेमी² एवं 81 सेमी² हैं। यदि बड़े त्रिभुज की बड़ी भुजा की लम्बाई 36 सेमी है तो छोटे त्रिभुज की बड़ी भुजा की लम्बाई ज्ञात कीजिए।
- हल:
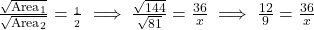
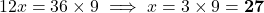 सेमी.
सेमी.
प्र.18 दो समरूप त्रिभुज ![]() और
और ![]() में यदि
में यदि ![]() तो
तो ![]() का मान ज्ञात कीजिए।
का मान ज्ञात कीजिए।
- हल: समरूपता से,
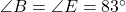 .
. में:
में:  .
.
प्र.19 यदि ![]() तथा
तथा ![]() cm एवं
cm एवं ![]() cm यदि
cm यदि ![]() का परिमाप 25 cm तो
का परिमाप 25 cm तो ![]() का परिमाप क्या है?
का परिमाप क्या है?
- हल:
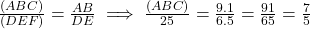
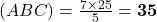 सेमी.
सेमी.
प्र.20 दो समरूप त्रिभुजों ![]() एवं
एवं ![]() में यदि
में यदि ![]() cm,
cm, ![]() CM और
CM और ![]() का क्षेत्रफल 54 cm² है तो
का क्षेत्रफल 54 cm² है तो ![]() का क्षेत्रफल क्या होगा?
का क्षेत्रफल क्या होगा?
- हल:
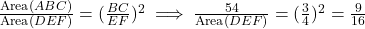
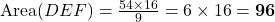 सेमी²
सेमी²
प्र.21 ![]() में
में ![]() एवं
एवं ![]() . यदि
. यदि ![]() तो
तो ![]() का माप ज्ञात कीजिए।
का माप ज्ञात कीजिए।
- हल: थेल्स प्रमेय से
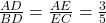 .
.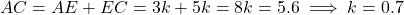 .
.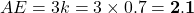 सेमी.
सेमी.
प्र.22 यदि कोई रेखा एक त्रिभुज ![]() की भुजाओं
की भुजाओं ![]() और
और ![]() को क्रमशः
को क्रमशः ![]() और
और ![]() पर प्रतिच्छेद करे तथा भुजा
पर प्रतिच्छेद करे तथा भुजा ![]() के समांतर हो, तो सिद्ध कीजिए कि
के समांतर हो, तो सिद्ध कीजिए कि ![]() होगा?
होगा?
- हल:
- दिया है
 .
. - थेल्स प्रमेय (BPT) से:
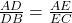 .
. - व्युत्क्रम लेने पर:
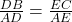 .
. - दोनों पक्षों में 1 जोड़ने पर:
 .
. 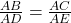 .
.- पुनः व्युत्क्रम लेने पर:
 . (इति सिद्धम)
. (इति सिद्धम)
- दिया है
प्र.23 आकृति में ![]() है तथा
है तथा ![]() है। सिद्ध कीजिए कि
है। सिद्ध कीजिए कि ![]() एक समद्विबाहु त्रिभुज है।
एक समद्विबाहु त्रिभुज है।
- हल:
- दिया है:
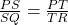 .
. - थेल्स प्रमेय के विलोम से,
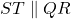 .
. - चूँकि
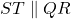 , अतः संगत कोण बराबर होंगे:
, अतः संगत कोण बराबर होंगे:  .
. - दिया है:
 .
. - (3) और (4) से:
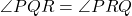 .
. 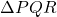 में, बराबर कोणों की सम्मुख भुजाएँ बराबर होती हैं:
में, बराबर कोणों की सम्मुख भुजाएँ बराबर होती हैं:  .
.- अतः,
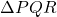 एक समद्विबाहु त्रिभुज है। (इति सिद्धम)
एक समद्विबाहु त्रिभुज है। (इति सिद्धम)
- दिया है:
प्र.24 ![]() एक समलंब चतुर्भुज है जिसमें
एक समलंब चतुर्भुज है जिसमें ![]() है तथा इसके विकर्ण परस्पर बिंदु
है तथा इसके विकर्ण परस्पर बिंदु ![]() पर प्रतिच्छेद करते हैं। दर्शाइए कि
पर प्रतिच्छेद करते हैं। दर्शाइए कि ![]() है।
है।
- हल:
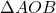 और
और 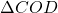 में:
में:
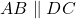 , अतः
, अतः 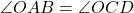 (एकांतर अंतः कोण).
(एकांतर अंतः कोण).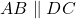 , अतः
, अतः 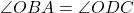 (एकांतर अंतः कोण).
(एकांतर अंतः कोण).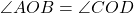 (शीर्षाभिमुख कोण).
(शीर्षाभिमुख कोण).- अतः,
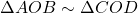 (AAA समरूपता).
(AAA समरूपता). 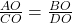 (समरूप त्रिभुजों की संगत भुजाएँ).
(समरूप त्रिभुजों की संगत भुजाएँ).- (Alternendo)
 . (इति सिद्धम)
. (इति सिद्धम)
प्र.25 आकृति में ![]() है। सिद्ध कीजिए कि
है। सिद्ध कीजिए कि ![]() है।
है।
- हल:
- समकोण
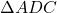 में:
में:  (i)
(i) - समकोण
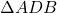 में:
में: 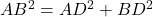 (ii)
(ii) 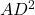 का मान (i) से (ii) में रखने पर:
का मान (i) से (ii) में रखने पर: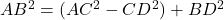
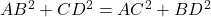 . (इति सिद्धम)
. (इति सिद्धम)
- समकोण
प्र.27 एक चतुर्भुज ![]() के विकर्ण परस्पर बिंदु
के विकर्ण परस्पर बिंदु ![]() पर इस प्रकार प्रतिच्छेद करते हैं कि
पर इस प्रकार प्रतिच्छेद करते हैं कि ![]() है। दर्शाइए कि
है। दर्शाइए कि ![]() एक समलंब चतुर्भुज है।
एक समलंब चतुर्भुज है।
- हल:
- दिया है:
 . इसे
. इसे 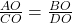 लिख सकते हैं।
लिख सकते हैं। 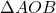 और
और 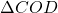 में:
में:
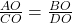 (दिया है)
(दिया है)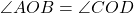 (शीर्षाभिमुख कोण)
(शीर्षाभिमुख कोण)
- अतः,
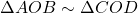 (SAS समरूपता).
(SAS समरूपता). - इसलिए,
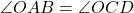 .
. - चूँकि ये
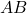 और
और 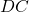 के लिए एकांतर अंतः कोण हैं, अतः
के लिए एकांतर अंतः कोण हैं, अतः 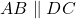 .
. - अतः,
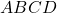 एक समलंब चतुर्भुज है। (इति सिद्धम)
एक समलंब चतुर्भुज है। (इति सिद्धम)
- दिया है:
प्र.28 एक समलंब ![]() जिसमें
जिसमें ![]() है के विकर्ण
है के विकर्ण ![]() पर प्रतिच्छेद करते हैं। यदि
पर प्रतिच्छेद करते हैं। यदि ![]() हो तो
हो तो ![]() और
और ![]() के क्षेत्रफलों का अनुपात ज्ञात कीजिए।
के क्षेत्रफलों का अनुपात ज्ञात कीजिए।
- हल: चूँकि
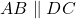 ,
, 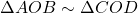 (जैसा प्र.24 में सिद्ध किया गया)।
(जैसा प्र.24 में सिद्ध किया गया)।
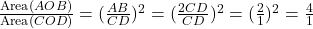 .
.- अनुपात = 4 : 1.
प्र.29 ![]() एक समद्विबाहु त्रिभुज है जिसका कोण
एक समद्विबाहु त्रिभुज है जिसका कोण ![]() समकोण है सिद्ध कीजिये कि
समकोण है सिद्ध कीजिये कि ![]() है।
है।
- हल:
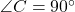 पर पाइथागोरस प्रमेय से:
पर पाइथागोरस प्रमेय से: 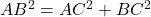 .
.- समद्विबाहु होने के कारण (और
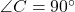 ),
),  .
.  को
को  से प्रतिस्थापित करने पर:
से प्रतिस्थापित करने पर: 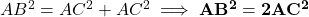 . (इति सिद्धम)
. (इति सिद्धम)
प्र.30 एक त्रिभुज ![]() की भुजा
की भुजा ![]() पर एक बिंदु
पर एक बिंदु ![]() इस प्रकार स्थित है कि
इस प्रकार स्थित है कि ![]() है। दर्शाइए कि
है। दर्शाइए कि ![]() है।
है।
- हल:
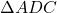 और
और 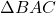 में:
में:
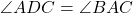 (दिया है).
(दिया है).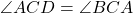 (उभयनिष्ठ कोण C).
(उभयनिष्ठ कोण C).- अतः,
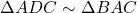 (AA समरूपता).
(AA समरूपता). - संगत भुजाएँ:
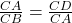 .
. - तिर्यक गुणा करने पर:
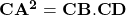 . (इति सिद्धम)
. (इति सिद्धम)
प्र.31 आकृति में यदि ![]() ,
, ![]() एवं
एवं ![]() तो
तो ![]() और
और ![]() के मान ज्ञात करो।
के मान ज्ञात करो।
- हल:
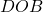 एक सीधी रेखा है:
एक सीधी रेखा है: 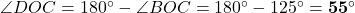 .
.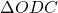 में:
में: 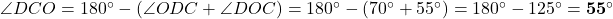 .
.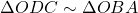 , अतः
, अतः 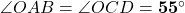 .
.
प्र.32 90 सेमी की लड़की बल्ब लगे खंभे के आधार से 1.2 m/s की चाल से चल रही है। यदि बल्ब 3.6 m की ऊँचाई पर है तो 4 सेकंड बाद लड़की की छाया की लंबाई ज्ञात कीजिए।
- हल: 4 सेकंड में लड़की द्वारा चली गई दूरी =
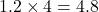 मी.
मी.
- खंभे की ऊँचाई = 3.6 मी; लड़की की ऊँचाई = 0.9 मी.
- माना छाया की लंबाई
 है।
है। - समरूप त्रिभुजों (AA) से:

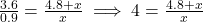
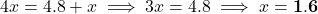 मी.
मी.
प्र.33 एक हवाई जहाज अड्डे से उत्तर की ओर 1000 km/hr की चाल से उड़ता है। इसी समय एक अन्य जहाज पश्चिम की ओर 1200 km/hr की चाल से उड़ता है। ![]() घंटे बाद दोनों जहाजों के बीच की दूरी कितनी होगी?
घंटे बाद दोनों जहाजों के बीच की दूरी कितनी होगी?
- हल:
 घंटे में,
घंटे में,
- उत्तर की दूरी =
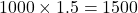 किमी.
किमी. - पश्चिम की दूरी =
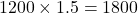 किमी.
किमी. 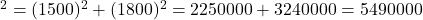
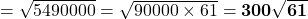 किमी.
किमी.
- उत्तर की दूरी =
प्र.34 आधारभूत समानुपातिकता (थेल्स प्रमेय) का कथन लिखो एवं सिद्ध करो।
- कथन: (प्र.4 (3) देखें)। सिद्ध करना: (यह एक मानक प्रमेय है, कृपया पाठ्यपुस्तक देखें।)
प्र.35 ![]() और
और ![]() त्रिभुजों
त्रिभुजों ![]() और
और ![]() की क्रमशः माध्यिकाएँ है जबकि
की क्रमशः माध्यिकाएँ है जबकि ![]() है। सिद्ध कीजिये कि
है। सिद्ध कीजिये कि ![]() है।
है।
- हल:
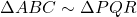 , अतः
, अतः  और
और 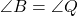 .
.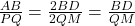 (चूँकि
(चूँकि 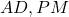 माध्यिकाएँ हैं)।
माध्यिकाएँ हैं)।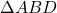 और
और 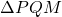 में:
में: 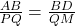 और
और 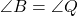 .
.- अतः
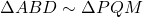 (SAS समरूपता).
(SAS समरूपता). 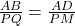 . (इति सिद्धम)
. (इति सिद्धम)
प्र.36 यदि दो समरूप त्रिभुजों के क्षेत्रफल बराबर हों तो सिद्ध कीजिये कि वे त्रिभुज सर्वांगसम होते हैं।
- हल:
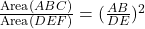 . यदि क्षेत्रफल बराबर हैं, तो
. यदि क्षेत्रफल बराबर हैं, तो 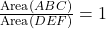 .
.
 .
.- इसी प्रकार,
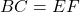 और
और 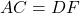 .
. - SSS सर्वांगसमता से,
 . (इति सिद्धम)
. (इति सिद्धम)
प्र.37 सिद्ध कीजिये दो समरूप त्रिभुजों के क्षेत्रफलों का अनुपात इनकी संगत भुजाओं के अनुपात के वर्ग के बराबर होता है।
- कथन: (यह एक मानक प्रमेय है, कृपया पाठ्यपुस्तक देखें।)
प्र.38 सिद्ध कीजिये एक समकोण त्रिभुज में कर्ण का वर्ग शेष दो भुजाओं के वर्गों के योग के बराबर होता है। (पाइथागोरस प्रमेय)
- कथन: (यह एक मानक प्रमेय है, कृपया पाठ्यपुस्तक देखें।)
प्र.39 यदि किसी त्रिभुज की एक भुजा का वर्ग अन्य दो भुजाओं के वर्गों के योग के बराबर हो तो पहली भुजा का सम्मुख कोण समकोण होता है। (पाइथागोरस का विलोम)
- कथन: (यह एक मानक प्रमेय है, कृपया पाठ्यपुस्तक देखें।)
प्र.40 किसी समबाहु त्रिभुज में, सिद्ध कीजिए कि उसकी एक भुजा के वर्ग का तिगुना उसके एक शीर्ष लंब के वर्ग के चार गुने के बराबर होता है।
- हल: (यह प्र.1 (MCQ) 13 के समान है।)
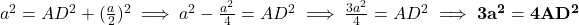 . (इति सिद्धम)
. (इति सिद्धम)
प्र.41 ![]() एक समकोण त्रिभुज है जिसका कोण
एक समकोण त्रिभुज है जिसका कोण ![]() समकोण है तथा
समकोण है तथा ![]() पर बिंदु
पर बिंदु ![]() इस प्रकार स्थित है कि
इस प्रकार स्थित है कि ![]() है। दर्शाइए कि
है। दर्शाइए कि ![]() है।
है।
- हल:
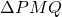 और
और 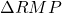 में:
में: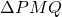 में,
में, 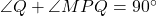 .
.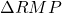 में,
में, 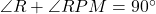 .
.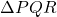 में,
में, 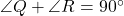 .
.- (2) और (4) से
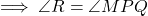 .
. - (3) और (4) से
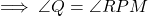 .
. - अतः
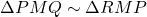 (AA समरूपता).
(AA समरूपता).  . (इति सिद्धम)
. (इति सिद्धम)