MP Board 10th Quadratic Equation Question Bank अध्याय 4: द्विघात समीकरण
स्मरणीय बिंदु
- चर
 में एक द्विघात समीकरण
में एक द्विघात समीकरण  के रूप में होती है, जहाँ
के रूप में होती है, जहाँ  वास्तविक संख्याएँ हैं तथा
वास्तविक संख्याएँ हैं तथा  है।उदाहरण के लिए,
है।उदाहरण के लिए, 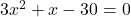 एक द्विघात समीकरण है।
एक द्विघात समीकरण है। - “कोई भी समीकरण
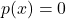 , जहाँ
, जहाँ  , घात 2 का एक बहुपद है, एक द्विघात समीकरण कहलाती है।” यदि समीकरण
, घात 2 का एक बहुपद है, एक द्विघात समीकरण कहलाती है।” यदि समीकरण 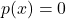 , जहाँ
, जहाँ  , घात 2 का एक बहुपद है, में
, घात 2 का एक बहुपद है, में  के पद घातों के घटते क्रम में लिखे जायें तो समीकरण का मानक रूप (Standard Form) प्राप्त होता है। अर्थात्
के पद घातों के घटते क्रम में लिखे जायें तो समीकरण का मानक रूप (Standard Form) प्राप्त होता है। अर्थात् 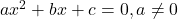 , द्विघात समीकरण का मानक रूप (Standard Form) है।
, द्विघात समीकरण का मानक रूप (Standard Form) है। - हम जानते हैं कि यदि वास्तविक संख्या
 बहुपद
बहुपद 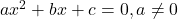 का एक शून्यक कहलाती है, यदि
का एक शून्यक कहलाती है, यदि 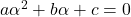 हो। इसी प्रकार से वास्तविक संख्या
हो। इसी प्रकार से वास्तविक संख्या  समीकरण
समीकरण 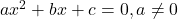 का एक मूल कहलाती है, यदि
का एक मूल कहलाती है, यदि 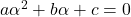 हो।
हो। - एक द्विघात बहुपद के अधिक से अधिक दो शून्यक हो सकते हैं। अतः किसी द्विघात समीकरण के भी अधिक से अधिक दो मूल हो सकते हैं।
- द्विघात बहुपद
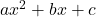 के शून्यक एवं द्विघात समीकरण
के शून्यक एवं द्विघात समीकरण  के मूल एक ही होते हैं।
के मूल एक ही होते हैं। - यदि हम
 के दो रैखिक गुणकों में गुणनखंड कर सकें तो द्विघात समीकरण
के दो रैखिक गुणकों में गुणनखंड कर सकें तो द्विघात समीकरण  के मूल प्रत्येक गुणनखंड को शून्य के बराबर करके प्राप्त कर सकते हैं।
के मूल प्रत्येक गुणनखंड को शून्य के बराबर करके प्राप्त कर सकते हैं। - द्विघात समीकरण
 के मूल
के मूल  होते हैं। यहाँ
होते हैं। यहाँ  यह निश्चित करता है कि समीकरण के मूल वास्तविक हैं या नहीं।
यह निश्चित करता है कि समीकरण के मूल वास्तविक हैं या नहीं।  को समीकरण का विविक्तकर (Discriminant) कहते हैं तथा इसे
को समीकरण का विविक्तकर (Discriminant) कहते हैं तथा इसे 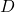 से निरूपित करते हैं। अर्थात्
से निरूपित करते हैं। अर्थात्  .
. - द्विघात समीकरण
 के(i) दो भिन्न वास्तविक मूल होते हैं, यदि
के(i) दो भिन्न वास्तविक मूल होते हैं, यदि 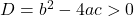 हो।(ii) दो बराबर वास्तविक मूल होते हैं, यदि
हो।(ii) दो बराबर वास्तविक मूल होते हैं, यदि 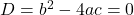 हो।(iii) कोई वास्तविक मूल नहीं होता है, यदि
हो।(iii) कोई वास्तविक मूल नहीं होता है, यदि 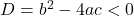 हो।
हो।
प्र.1 सही विकल्प चुनिए।
1. यदि द्विघात समीकरण ![]() के मूल समान हों तो समीकरण के विविक्तकर का मान होगा:
के मूल समान हों तो समीकरण के विविक्तकर का मान होगा:
(A) 0
(B) 1
(C) 2
(D) 3
- हल: द्विघात समीकरण के मूल समान (बराबर) होने की शर्त है कि उसका विविक्तकर (Discriminant,
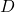 ) शून्य के बराबर हो।
) शून्य के बराबर हो। - सही विकल्प: (A) 0
2. समीकरण ![]() के मूलों की प्रकृति होगी:
के मूलों की प्रकृति होगी:
(A) वास्तविक और समान
(B) वास्तविक और भिन्न
(C) कोई वास्तविक मूल नहीं
(D) इनमें से कोई नहीं
- हल: प्रकृति ज्ञात करने के लिए हम विविक्तकर
 ज्ञात करेंगे।
ज्ञात करेंगे।
यहाँ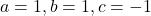
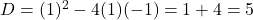
चूंकि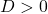 (5 > 0), मूल वास्तविक और भिन्न होंगे।
(5 > 0), मूल वास्तविक और भिन्न होंगे। - सही विकल्प: (B) वास्तविक और भिन्न
3. किसी द्विघात समीकरण में चर कि अधिकतम घात होती है:
(A) 1
(B) 2
(C) 3
(D) 4
- हल: “द्विघात” (Quadratic) समीकरण का अर्थ ही है कि चर की अधिकतम घात 2 हो।
- सही विकल्प: (B) 2
4. द्विघात समीकरण ![]() का विविक्तकर होगा:
का विविक्तकर होगा:
(A) ![]()
(B) ![]()
(C) ![]()
(D) ![]()
- हल: विविक्तकर (Discriminant) का मानक सूत्र
 है।
है। - सही विकल्प: (A)

5. निम्नलिखित में से किस द्विघात समीकरण के मूल वास्तविक होंगे:
(A) ![]()
(B) ![]()
(C) ![]()
(D) ![]()
- हल: मूल वास्तविक होने के लिए
 (विविक्तकर 0 या 0 से बड़ा) होना चाहिए।
(विविक्तकर 0 या 0 से बड़ा) होना चाहिए।
(A)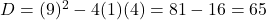 . (
. (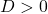 )
)
(B)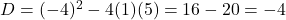 . (
. (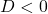 )
)
(C)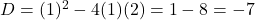 . (
. (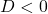 )
)
(D)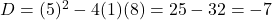 . (
. (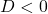 )
)
केवल (A) में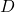 धनात्मक है, अतः इसके मूल वास्तविक होंगे।
धनात्मक है, अतः इसके मूल वास्तविक होंगे। - सही विकल्प: (A)

6. द्विघात समीकरण ![]() के मूल होंगे:
के मूल होंगे:
(A) ![]()
(B) ![]()
(C) ![]()
(D) ![]()
- हल: गुणनखंड करने पर:
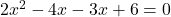
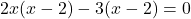
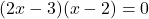
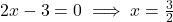
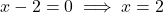
- सही विकल्प: (A)

7. निम्न में कौन एक वर्ग समीकरण नहीं है?
(A) ![]()
(B) ![]()
(C) ![]()
(D) ![]()
- हल: वर्ग समीकरण (द्विघात समीकरण) में
 की अधिकतम घात 2 होनी चाहिए।
की अधिकतम घात 2 होनी चाहिए।
(A)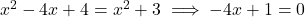 . (यह रैखिक है, द्विघात नहीं)
. (यह रैखिक है, द्विघात नहीं)
(B)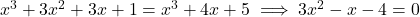 . (यह द्विघात है)
. (यह द्विघात है)
(C)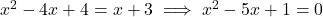 . (यह द्विघात है)
. (यह द्विघात है)
(D)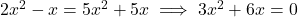 . (यह द्विघात है)
. (यह द्विघात है) - सही विकल्प: (A)
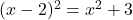
8. यदि ![]() वर्ग समीकरण
वर्ग समीकरण ![]() का एक मूल है, तो
का एक मूल है, तो ![]() का मान होगा:
का मान होगा:
(A) ![]()
(B) ![]()
(C) ![]()
(D) ![]()
- हल: यदि
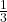 एक मूल है, तो
एक मूल है, तो 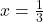 रखने पर समीकरण संतुष्ट होगा।
रखने पर समीकरण संतुष्ट होगा।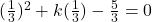
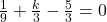
(पूरे समीकरण को 9 से गुणा करने पर)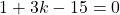
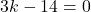
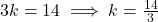
- सही विकल्प: (B)

9. ![]() के किस मान के लिये वर्ग समीकरण
के किस मान के लिये वर्ग समीकरण ![]() के दोनों मूल बराबर होंगे:
के दोनों मूल बराबर होंगे:
(A) 4 और 0
(B) 1 और 4
(C) 0 और 1
(D) 0 और 4
- हल: मूल बराबर होने के लिए
 होना चाहिए।
होना चाहिए।
यहाँ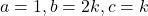
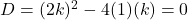
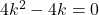
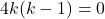
अतः
या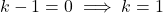
- सही विकल्प: (C) 0 और 1
10. द्विघात समीकरण ![]() के विविक्तकर का मान होगा:
के विविक्तकर का मान होगा:
(A) 28
(B) 16
(C) 64
(D) 100
- हल:

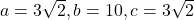
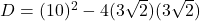
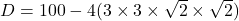
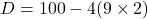
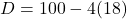

- सही विकल्प: (A) 28
11. द्विघात समीकरण ![]() के मूल होंगे:
के मूल होंगे:
(A) वास्तविक
(B) काल्पनिक
(C) वास्तविक और काल्पनिक दोनों
(D) इनमें से कोई नहीं
- हल: मूलों की प्रकृति
 पर निर्भर करती है।
पर निर्भर करती है।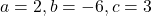
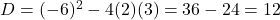
चूंकि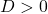 (12 > 0), मूल वास्तविक होंगे।
(12 > 0), मूल वास्तविक होंगे। - सही विकल्प: (A) वास्तविक
12. द्विघात समीकरण में मूलों की अधिकतम संख्या होती है।
(A) 0
(B) 2
(C) 1
(D) 3
- हल: द्विघात (घात 2) समीकरण के अधिकतम दो मूल हो सकते हैं।
- सही विकल्प: (B) 2
13. समीकरण ![]() के हल हैं:
के हल हैं:
(A) -1, -1
(B) 0, 0
(C) 1, 1
(D) -1, 1
- हल:

वर्गमूल लेने पर: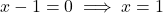
चूंकि यह द्विघात समीकरण है, इसके दो मूल होंगे जो दोनों बराबर हैं।
हल हैं 1, 1. - सही विकल्प: (C) 1, 1
14. वर्ग समीकरण ![]() के मूलों की प्रकृति है:
के मूलों की प्रकृति है:
(A) वास्तविक
(B) समान
(C) काल्पनिक
(D) इनमें से कोई नहीं
- हल:

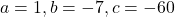
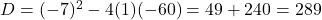
चूंकि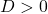 (289 > 0), मूल वास्तविक होंगे।
(289 > 0), मूल वास्तविक होंगे। - सही विकल्प: (A) वास्तविक
15. ![]() के मूल हैं:
के मूल हैं:
(A) 0, -5
(B) 0, 5
(C) 5, -5
(D) -5, -5
- हल:

 कॉमन लेने पर:
कॉमन लेने पर: 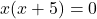
अतः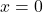
या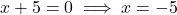
- सही विकल्प: (A) 0, -5
16. जब वर्ग समीकरण ![]() के मूल समान हों तब:
के मूल समान हों तब:
(A) ![]()
(B) ![]() (C)
(C) ![]()
(D) ![]()
- हल: मूल समान होने की शर्त है
 .
.
जिसका अर्थ है .
. - सही विकल्प: (D)

प्र.2 रिक्त स्थान की पूर्ति कीजिए।
- एक समीकरण
 , जहाँ
, जहाँ  घात 2 का बहुपद हो, द्विघात समीकरण कहलाती है।
घात 2 का बहुपद हो, द्विघात समीकरण कहलाती है। - किसी द्विघात समीकरण के अधिकतम दो मूल होते हैं।
- समीकरण
 के मूल 3, -4 हैं।
के मूल 3, -4 हैं। - यदि किसी द्विघात समीकरण के मूल वास्तविक और समान हों तो उस समीकरण के विविक्तकर का मान शून्य (0) होगा।
- द्विघात समीकरण
 के विविक्तकर का सूत्र है
के विविक्तकर का सूत्र है 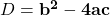
- द्विघात समीकरण से मूल ज्ञात करने का सूत्र प्राचीन भारतीय गणितज्ञ श्रीधराचार्य ने दिया था।
- द्विघात समीकरण का विविक्तकर ऋणात्मक हो, तो मूल काल्पनिक (या वास्तविक नहीं) होंगें।
- वर्ग समीकरण
 के मूल 1, -1 होंगें।
के मूल 1, -1 होंगें। - यदि
 एक द्विघात बहुपद है, तो
एक द्विघात बहुपद है, तो 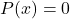 को द्विघात समीकरण कहते हैं।
को द्विघात समीकरण कहते हैं। - द्विघात समीकरण
 के मूल ज्ञात करने हेतु सूत्र है:
के मूल ज्ञात करने हेतु सूत्र है: 
- यदि
 हो, तो द्विघात समीकरण
हो, तो द्विघात समीकरण  के दोनों मूल समान (या बराबर) होते हैं।
के दोनों मूल समान (या बराबर) होते हैं। - द्विघात समीकरण
 के मूलों की प्रकृति वास्तविक और भिन्न होगी।
के मूलों की प्रकृति वास्तविक और भिन्न होगी।
- (हल:
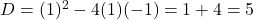 . चूँकि
. चूँकि 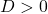 , मूल वास्तविक और भिन्न हैं।)
, मूल वास्तविक और भिन्न हैं।)
- (हल:
प्र.4 एक शब्द / वाक्य में उत्तर दीजिए।
- समीकरण
 में मान
में मान  क्या कहलाता है?
क्या कहलाता है?
- उत्तर: विविक्तकर (Discriminant)
- यदि किसी द्विघात समीकरण के मूल वास्तविक एवं समान हों तो उस समीकरण के विविक्तकर का मान कितना होगा?
- उत्तर: 0 (शून्य)
- यदि किसी द्विघात समीकरण के विविक्तकर का मान ऋणात्मक हो तो उस समीकरण के मूलों की प्रकृति कैसी होगी?
- उत्तर: काल्पनिक (या वास्तविक नहीं)
- यदि किसी द्विघात समीकरण के विविक्तकर का मान धनात्मक हो तो उस समीकरण के मूलों की प्रकृति कैसी होगी?
- उत्तर: वास्तविक और भिन्न
- वर्ग समीकरण का मानक रूप लिखिए।
- उत्तर:
 , जहाँ
, जहाँ 
- उत्तर:
- द्विघात समीकरण
 का विविक्तकर ज्ञात करने का सूत्र लिखिए।
का विविक्तकर ज्ञात करने का सूत्र लिखिए।
- उत्तर:

- उत्तर:
- यदि किसी वर्ग समीकरण का विविक्तकर धनात्मक पूर्ण वर्ग संख्या हो तो उसके मूल कैसे होंगे?
- उत्तर: वास्तविक, भिन्न और परिमेय
- वर्ग समीकरण
 के मूलों का योगफल क्या होगा?
के मूलों का योगफल क्या होगा?
- उत्तर: -4 (सूत्र:
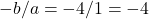 )
)
- उत्तर: -4 (सूत्र:
- वर्ग समीकरण
 के मूलों का गुणनफल क्या होगा?
के मूलों का गुणनफल क्या होगा?
- उत्तर: 3 (सूत्र:
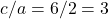 )
)
- उत्तर: 3 (सूत्र:
- समीकरण जिसमें चर की अधिकतम घात दो हो तो क्या कहलाता है?
- उत्तर: द्विघात समीकरण (या वर्ग समीकरण)
11. क्या ![]() एक द्विघात समीकरण है?
एक द्विघात समीकरण है?
- उत्तर: नहीं, क्योंकि इसमें चर
 की घात (
की घात (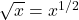 ) एक पूर्णांक नहीं है।
) एक पूर्णांक नहीं है।
12. द्विघात समीकरण ![]() के मूल क्या होंगें?
के मूल क्या होंगें?
- उत्तर:

- (हल:
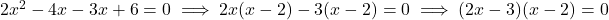 )
)
- (हल:
13. वर्ग समीकरण ![]() के मूलों का योग कितना होगा?
के मूलों का योग कितना होगा?
- उत्तर:
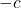 (सूत्र:
(सूत्र: 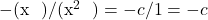 )
)
प्र.5 सत्य / असत्य लिखिए।
- एक द्विघात समीकरण के एक से अधिक मूल हो सकते हैं।
- उत्तर: सत्य (द्विघात समीकरण के दो मूल होते हैं, जो एक से अधिक है)
- समीकरण
 के मूल 0 और -1 होंगें।
के मूल 0 और -1 होंगें।
- उत्तर: असत्य (मूल 0 और 1 हैं)
- समीकरण
 के मूल समान होंगें।
के मूल समान होंगें।
- उत्तर: सत्य (
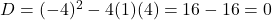 ,
, 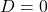 पर मूल समान होते हैं)
पर मूल समान होते हैं)
- उत्तर: सत्य (
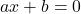 एक द्विघात समीकरण है।
एक द्विघात समीकरण है।
- उत्तर: असत्य (यह एक रैखिक समीकरण है)
- वर्ग समीकरण में चर की अधिकतम घात कुछ भी हो सकती है।
- उत्तर: असत्य (अधिकतम घात 2 होती है)
 में
में  के मान 0 और 1 हैं।
के मान 0 और 1 हैं।
- उत्तर: असत्य (
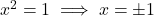 , मान 1 और -1 हैं)
, मान 1 और -1 हैं)
- उत्तर: असत्य (
- जब वर्ग समीकरण के दोनों मूल समान हों तब विविक्तकर
 होता है।
होता है।
- उत्तर: सत्य
- वर्ग समीकरण
 के मूलों का योगफल 2 है।
के मूलों का योगफल 2 है।
- उत्तर: असत्य (योगफल
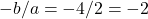 है)
है)
- उत्तर: असत्य (योगफल
- वर्ग समीकरण
 की सूत्र विधि गणितज्ञ पाइथागोरस द्वारा की गई है।
की सूत्र विधि गणितज्ञ पाइथागोरस द्वारा की गई है।
- उत्तर: असत्य (यह श्रीधराचार्य द्वारा दी गई है)
- वर्ग समीकरण के अनेक हल होते हैं।
- उत्तर: असत्य (केवल दो हल होते हैं)
- जब
 तो वर्ग समीकरण के मूल वास्तविक होते हैं।
तो वर्ग समीकरण के मूल वास्तविक होते हैं।
- उत्तर: सत्य (
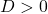 पर वास्तविक और भिन्न,
पर वास्तविक और भिन्न, 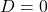 पर वास्तविक और समान)
पर वास्तविक और समान)
- उत्तर: सत्य (
प्र.3 सही जोड़ी बनाइए।
| स्तम्भ – A | स्तम्भ – B |
|---|---|
| (i) यदि किसी द्विघात समीकरण का विविक्तकर | (ब) तो मूल वास्तविक तथा भिन्न |
| (ii) यदि | (अ) |
| (iii) द्विघात समीकरण | (स) 1, -1 |
| (iv) द्विघात समीकरण | (इ) 0, 3 |
| (v) द्विघात समीकरण | (द) 3, 3 |
नोट: प्रश्न (i) ![]() का सही मिलान “मूल वास्तविक होते हैं” होना चाहिए। (ब) “मूल वास्तविक तथा भिन्न”
का सही मिलान “मूल वास्तविक होते हैं” होना चाहिए। (ब) “मूल वास्तविक तथा भिन्न” ![]() के लिए होता है। दिए गए विकल्पों में (ब) ही सबसे निकटतम है, संभवतः यह प्रश्न में
के लिए होता है। दिए गए विकल्पों में (ब) ही सबसे निकटतम है, संभवतः यह प्रश्न में ![]() होना चाहिए था।
होना चाहिए था।
यहाँ सभी छवियों में दिए गए प्रश्नों के हल क्रमबद्ध तरीके से दिए गए हैं:
प्र.6 जाँच कीजिए कि ![]() द्विघात समीकरण है या नहीं।
द्विघात समीकरण है या नहीं।
- हल:
समीकरण: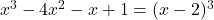
हम जानते हैं कि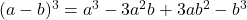
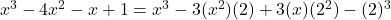
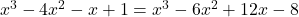
(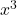 दोनों पक्षों से कट जाएगा)
दोनों पक्षों से कट जाएगा)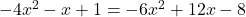
(सभी पदों को बाएँ पक्ष में लाने पर)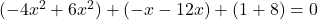
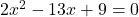
यह के रूप का है, जहाँ
के रूप का है, जहाँ 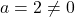 .
.
उत्तर: हाँ, यह एक द्विघात समीकरण है।
प्र.7 जाँच कीजिए कि ![]() द्विघात समीकरण है या नहीं।
द्विघात समीकरण है या नहीं।
- हल:
LHS: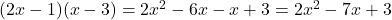
RHS: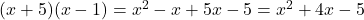
अब,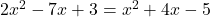
(सभी पदों को बाएँ पक्ष में लाने पर)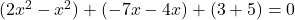
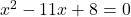
यह के रूप का है, जहाँ
के रूप का है, जहाँ 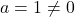 .
.
उत्तर: हाँ, यह एक द्विघात समीकरण है।
प्र.8 जाँच कीजिए कि ![]() द्विघात समीकरण है या नहीं।
द्विघात समीकरण है या नहीं।
- हल:
LHS: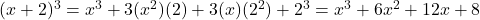
RHS: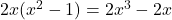
अब,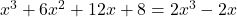
(सभी पदों को दाएँ पक्ष में लाने पर)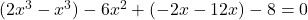
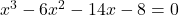
यहाँ चर की अधिकतम घात 3 है।
की अधिकतम घात 3 है।
उत्तर: नहीं, यह एक त्रिघात (cubic) समीकरण है, द्विघात नहीं।
प्र.9 स्थिति को गणितीय रूप में व्यक्त कीजिए: एक रेलगाड़ी 480 km की दूरी समान चाल से तय करती है। यदि इसकी चाल 8 km/h कम होती तो वह उसी दूरी को तय करने में 3 घंटे अधिक लेती।
- हल:
माना रेलगाड़ी की समान चाल = km/h
km/h
दूरी = 480 km
लिया गया समय (t₁) =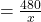 घंटे
घंटे
नई चाल =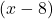 km/h
km/h
नया लिया गया समय (t₂) =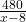 घंटे
घंटे
प्रश्नानुसार,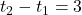 (नया समय 3 घंटे अधिक है)
(नया समय 3 घंटे अधिक है)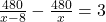
![Rendered by QuickLaTeX.com 480 \left[ \frac{1}{x - 8} - \frac{1}{x} \right] = 3](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-b3194b7ebf3887fa6dc9f75144325066_l3.png)
![Rendered by QuickLaTeX.com 480 \left[ \frac{x - (x - 8)}{x(x - 8)} \right] = 3](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-d69d2d1ccf9aff3dee126c4dfa2308ff_l3.png)
![Rendered by QuickLaTeX.com 480 \left[ \frac{8}{x^2 - 8x} \right] = 3](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-d50a5a9413009849ecd0a53ea324f988_l3.png)
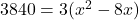
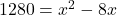
उत्तर (गणितीय रूप):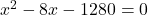
प्र.10 स्थिति को गणितीय रूप में व्यक्त कीजिए: दो क्रमागत धनात्मक पूर्णांकों का गुणनफल 306 है।
- हल:
माना पहला धनात्मक पूर्णांक =
दूसरा क्रमागत पूर्णांक =
प्रश्नानुसार, उनका गुणनफल 306 है।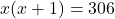
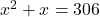
उत्तर (गणितीय रूप):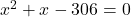
प्र.11 ![]() का ऐसा मान ज्ञात कीजिए जिससे
का ऐसा मान ज्ञात कीजिए जिससे ![]() के दो बराबर मूल हों।
के दो बराबर मूल हों।
- हल:
बराबर मूलों के लिए, विविक्तकर (Discriminant) होता है।
होता है।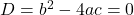
यहाँ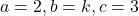
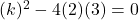
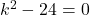
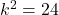
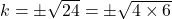
उत्तर: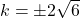
प्र.12 ![]() का ऐसा मान ज्ञात कीजिए जिससे
का ऐसा मान ज्ञात कीजिए जिससे ![]() के दो बराबर मूल हों।
के दो बराबर मूल हों।
- हल:
पहले समीकरण को मानक रूप में लिखें: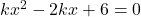
बराबर मूलों के लिए,
यहाँ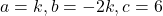
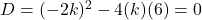
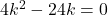
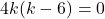
इससे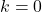 या
या 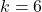 प्राप्त होता है।
प्राप्त होता है।
यदि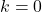 , तो समीकरण
, तो समीकरण 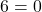 हो जाएगा, जो असंभव है। अतः
हो जाएगा, जो असंभव है। अतः  द्विघात समीकरण के लिए 0 नहीं हो सकता।
द्विघात समीकरण के लिए 0 नहीं हो सकता।
उत्तर: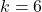
प्र.13 गुणनखंड विधि से ![]() को हल कीजिए।
को हल कीजिए।
- हल:
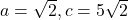 .
. 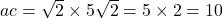
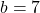 . हमें ऐसी दो संख्याएँ चाहिए जिनका गुणनफल 10 और योग 7 हो (वो हैं 5 और 2).
. हमें ऐसी दो संख्याएँ चाहिए जिनका गुणनफल 10 और योग 7 हो (वो हैं 5 और 2).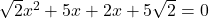
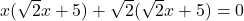
(ध्यान दें: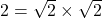 )
)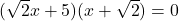
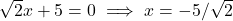
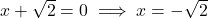
उत्तर: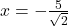 और
और 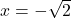
प्र.14 गुणनखंड विधि से ![]() को हल कीजिए।
को हल कीजिए।
- हल:
समीकरण को 8 से गुणा करने पर: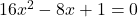
यह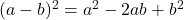 का रूप है।
का रूप है।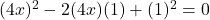
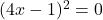
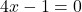
उत्तर: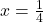 (दो समान मूल)
(दो समान मूल)
प्र.15 द्विघात समीकरण ![]() के मूल ज्ञात कीजिए।
के मूल ज्ञात कीजिए।
- हल:
(गुणनखंड विधि)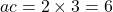 .
. 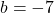 .
.
दो संख्याएँ जिनका गुणनफल 6 और योग -7 हो (वो हैं -6 और -1).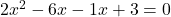
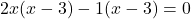
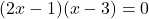
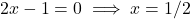
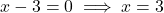
उत्तर: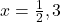
प्र.16 ![]() के मूल ज्ञात कीजिए?
के मूल ज्ञात कीजिए?
- हल:
 से गुणा करने पर (जहाँ
से गुणा करने पर (जहाँ 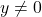 ):
):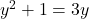
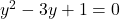
(यह गुणनखंड नहीं होगा, द्विघाती सूत्र का प्रयोग करें)
का प्रयोग करें)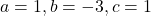
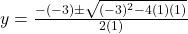
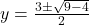
उत्तर: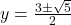
प्र.17 दो संख्याएँ ज्ञात कीजिए जिनका योग 17 तथा गुणनफल 72 हो।
- हल:
माना पहली संख्या =
दूसरी संख्या =
गुणनफल =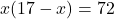
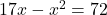
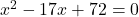
(गुणनखंड: योग -17, गुणनफल 72. वो हैं -8 और -9)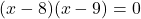
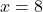 या
या 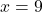
यदि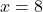 , दूसरी संख्या
, दूसरी संख्या 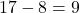 .
.
यदि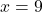 , दूसरी संख्या
, दूसरी संख्या 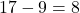 .
.
उत्तर: संख्याएँ 8 और 9 हैं।
प्र.18 दो क्रमागत धनात्मक पूर्णांक ज्ञात कीजिए जिनके वर्गों का योग 365 है।
- हल:
माना पहला पूर्णांक =
दूसरा पूर्णांक =
प्रश्नानुसार: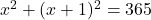
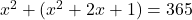
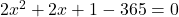
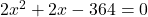
(2 से भाग देने पर)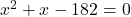
(गुणनखंड: योग 1, गुणनफल -182. वो हैं 14 और -13)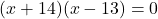
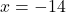 या
या 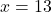
चूँकि पूर्णांक “धनात्मक” हैं,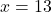
पहला पूर्णांक = 13, दूसरा = 13 + 1 = 14
उत्तर: संख्याएँ 13 और 14 हैं।
प्र.19 दो ऐसे क्रमागत सम पूर्णांक ज्ञात कीजिए जिनके वर्गों का योग 244 हो।
- हल:
माना पहला सम पूर्णांक =
दूसरा क्रमागत सम पूर्णांक =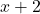
प्रश्नानुसार: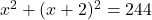
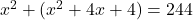
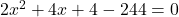
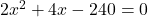
(2 से भाग देने पर)
(गुणनखंड: योग 2, गुणनफल -120. वो हैं 12 और -10)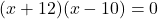
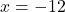 या
या 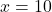
केस 1: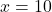 . संख्याएँ 10 और (10+2)=12.
. संख्याएँ 10 और (10+2)=12.
केस 2: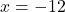 . संख्याएँ -12 और (-12+2)=-10.
. संख्याएँ -12 और (-12+2)=-10.
उत्तर: संख्याएँ 10, 12 या -12, -10 हैं। (यदि “धनात्मक” कहा जाता, तो केवल 10, 12 होता)
प्र.20 समीकरण ![]() का विविक्तकर ज्ञात कीजिए और मूलों की प्रकृति ज्ञात कीजिए, यदि वे वास्तविक हैं तो उन्हें ज्ञात कीजिए।
का विविक्तकर ज्ञात कीजिए और मूलों की प्रकृति ज्ञात कीजिए, यदि वे वास्तविक हैं तो उन्हें ज्ञात कीजिए।
- हल:
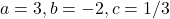
- विविक्तकर (D):
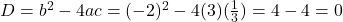
- मूलों की प्रकृति:
चूँकि , मूल वास्तविक और समान (बराबर) हैं।
, मूल वास्तविक और समान (बराबर) हैं। - मूल:
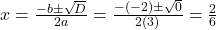
उत्तर: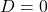 , मूल वास्तविक और समान हैं, जो
, मूल वास्तविक और समान हैं, जो 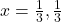 हैं।
हैं।
- विविक्तकर (D):
प्र.21 ‘k’ का ऐसा मान ज्ञात कीजिए जिसके लिए वर्ग समीकरण ![]() के दोनों मूल समान हों।
के दोनों मूल समान हों।
- हल:
(यह प्रश्न 12 के समान है)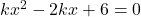
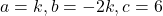
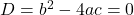
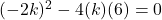

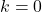 (असंभव) या
(असंभव) या 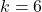
उत्तर: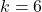
प्र.22 सूत्र विधि से ![]() के मूल ज्ञात कीजिए।
के मूल ज्ञात कीजिए।
- हल:
(यह प्रश्न 15 के समान है, पर विधि भिन्न है)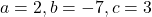

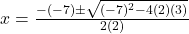
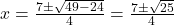
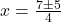
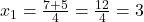
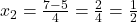
उत्तर: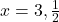
प्र.23 वर्ग समीकरण ![]() के मूल सूत्र विधि से ज्ञात कीजिए।
के मूल सूत्र विधि से ज्ञात कीजिए।
- हल:
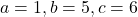

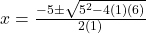

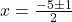
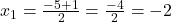
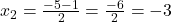
उत्तर: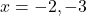
प्र.24 ![]() का हल कीजिए।
का हल कीजिए।
- हल:
(लघुत्तम समापवर्त्य (LCM) लेने पर)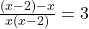
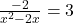
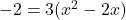
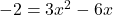
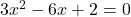
(सूत्र विधि का प्रयोग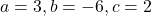 )
)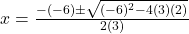
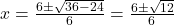
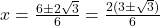
उत्तर: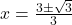
प्र.25 एक रेलगाड़ी 360 km की दूरी तय करती है। यदि चाल 5 km/h अधिक होती, तो यात्रा में 1 घंटा कम समय लगता। रेलगाड़ी की चाल ज्ञात कीजिए।
- हल:
माना रेलगाड़ी की समान चाल = km/h
km/h
दूरी = 360 km
सामान्य समय (t₁) =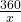
नई चाल =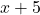
नया समय (t₂) =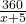
प्रश्नानुसार,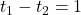 (पुराना समय 1 घंटा अधिक है)
(पुराना समय 1 घंटा अधिक है)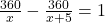
![Rendered by QuickLaTeX.com 360 \left[ \frac{(x + 5) - x}{x(x + 5)} \right] = 1](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-7c21ad73b0a0536377823f6ab1d1aac7_l3.png)
![Rendered by QuickLaTeX.com 360 \left[ \frac{5}{x^2 + 5x} \right] = 1](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-3e2cf3815948c9eb6aeb79156f07ca65_l3.png)
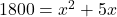
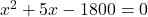
(गुणनखंड: योग 5, गुणनफल -1800. वो हैं 45 और -40)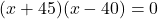
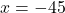 या
या 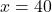
चाल ऋणात्मक नहीं हो सकती।
उत्तर: रेलगाड़ी की चाल 40 km/h है।
प्र.26 ![]() के मूलों का अस्तित्व हो तो उन्हें पूर्ण वर्ग विधि द्वारा ज्ञात कीजिए।
के मूलों का अस्तित्व हो तो उन्हें पूर्ण वर्ग विधि द्वारा ज्ञात कीजिए।
- हल:
(अस्तित्व जाँच: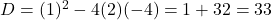 .
. 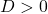 , मूल वास्तविक हैं)
, मूल वास्तविक हैं)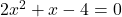
(2 से भाग दें)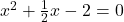
(स्थिरांक को दाईं ओर ले जाएँ)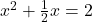
( के गुणांक
के गुणांक 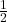 का आधा
का आधा 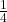 है, और
है, और 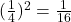 है। दोनों ओर
है। दोनों ओर 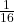 जोड़ें)
जोड़ें)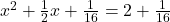
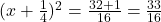
(वर्गमूल लेने पर)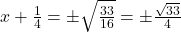
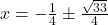
उत्तर: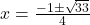
प्र.27 एक समकोण त्रिभुज की ऊँचाई उसके आधार से 7 सेमी कम है। यदि कर्ण 13 सेमी का हो, तो अन्य दो भुजाएँ ज्ञात कीजिए।
- हल:
माना आधार = cm
cm
ऊँचाई =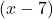 cm
cm
कर्ण = 13 cm
पाइथागोरस प्रमेय से: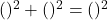
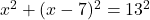
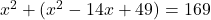
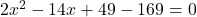
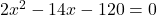
(2 से भाग देने पर)
(गुणनखंड: योग -7, गुणनफल -60. वो हैं -12 और 5)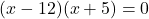
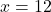 या
या 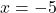
भुजा ऋणात्मक नहीं हो सकती, अतः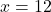 .
.
आधार = 12 cm
ऊँचाई =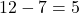 cm
cm
उत्तर: अन्य दो भुजाएँ 5 cm और 12 cm हैं।
प्र.28 पूर्ण वर्ग विधि से ![]() के मूल ज्ञात कीजिए।
के मूल ज्ञात कीजिए।
- हल:
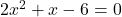
(2 से भाग दें)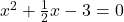
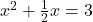
(दोनों ओर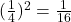 जोड़ें)
जोड़ें)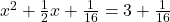
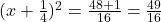
(वर्गमूल लेने पर)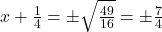
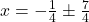
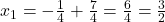
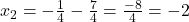
उत्तर: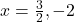
प्र.29 पूर्ण वर्ग विधि से ![]() के मूल ज्ञात कीजिए।
के मूल ज्ञात कीजिए।
- हल:
(पहले अस्तित्व जाँचें)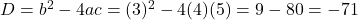
चूँकि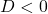 , समीकरण के कोई वास्तविक मूल नहीं हैं।
, समीकरण के कोई वास्तविक मूल नहीं हैं।
उत्तर: कोई वास्तविक मूल नहीं हैं।
प्र.30 ![]() के मूल ज्ञात कीजिए।
के मूल ज्ञात कीजिए।
- हल:
 से गुणा करने पर:
से गुणा करने पर: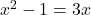
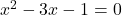
(सूत्र विधि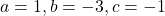 )
)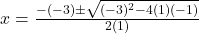
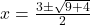
उत्तर: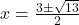
प्र.31 3 वर्ष पूर्व राजेश की आयु का व्युत्क्रम और अब से 5 वर्ष पश्चात आयु के व्युत्क्रम का योग ![]() है। उसकी वर्तमान आयु ज्ञात कीजिए।
है। उसकी वर्तमान आयु ज्ञात कीजिए।
- हल:
माना राजेश की वर्तमान आयु = वर्ष
वर्ष
3 वर्ष पूर्व आयु =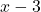 , व्युत्क्रम =
, व्युत्क्रम = 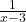
5 वर्ष पश्चात आयु =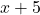 , व्युत्क्रम =
, व्युत्क्रम = 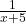
प्रश्नानुसार: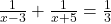
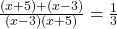
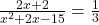
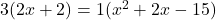
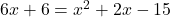
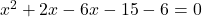
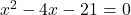
(गुणनखंड: योग -4, गुणनफल -21. वो हैं -7 और 3)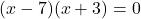
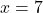 या
या 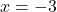
आयु ऋणात्मक नहीं हो सकती।
उत्तर: राजेश की वर्तमान आयु 7 वर्ष है।
प्र.32 एक कुटीर उद्योग बर्तनों का निर्माण करता है। एक विशेष दिन प्रत्येक नग की निर्माण लागत (₹ में) उस दिन के निर्माण किए बर्तनों की संख्या के दोगुने से 3 अधिक थी। यदि कुल निर्माण लागत ₹ 90 थी, तो निर्मित बर्तनों की संख्या और प्रत्येक नग की लागत ज्ञात कीजिए।
- हल:
माना निर्मित बर्तनों की संख्या =
प्रत्येक नग की लागत =
कुल लागत = (संख्या)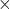 (लागत)
(लागत)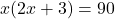
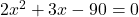
(सूत्र विधि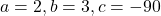 )
)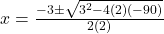
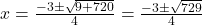
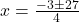
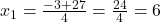
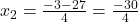 (असंभव, संख्या ऋणात्मक नहीं हो सकती)
(असंभव, संख्या ऋणात्मक नहीं हो सकती)
बर्तनों की संख्या =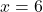
प्रत्येक नग की लागत =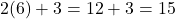
उत्तर: बर्तनों की संख्या = 6, प्रत्येक नग की लागत = ₹15
प्र.33 एक आयताकार खेत का विकर्ण उसकी छोटी भुजा से 60 मी अधिक लंबा है। यदि बड़ी भुजा छोटी भुजा से 30 मी अधिक हो, तो खेत की भुजाएँ ज्ञात कीजिए।
- हल:
माना छोटी भुजा (चौड़ाई) = m
m
बड़ी भुजा (लंबाई) =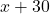 m
m
विकर्ण =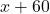 m
m
पाइथागोरस प्रमेय से: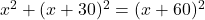
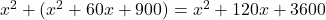
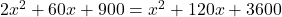

(गुणनखंड: योग -60, गुणनफल -2700. वो हैं -90 और 30)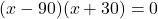
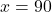 या
या 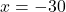 (असंभव)
(असंभव)
छोटी भुजा =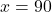 m
m
बड़ी भुजा =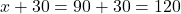 m
m
उत्तर: खेत की भुजाएँ 90 m और 120 m हैं।
प्र.34 दो संख्याओं के वर्गों का अंतर 180 है। छोटी संख्या का वर्ग बड़ी संख्या का आठ गुना है। दोनों संख्याएँ ज्ञात कीजिए।
- हल:
माना बड़ी संख्या = , छोटी संख्या =
, छोटी संख्या = 
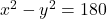 (समीकरण 1)
(समीकरण 1)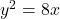 (समीकरण 2)
(समीकरण 2)
(समीकरण 2 का मान 1 में रखने पर)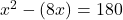

(गुणनखंड: योग -8, गुणनफल -180. वो हैं -18 और 10)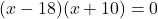
केस 1: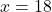
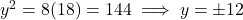
केस 2: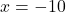
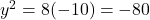 (वास्तविक नहीं, असंभव)
(वास्तविक नहीं, असंभव)
उत्तर: संख्याएँ 18, 12 या 18, -12 हैं।
प्र.35 दो पानी के नल एक साथ हौज को ![]() घंटों में भर सकते हैं। बड़े व्यास वाला नल हौज को भरने में, कम व्यास वाले नल से 10 घंटे कम समय लेता है। प्रत्येक द्वारा अलग से हौज को भरने का समय ज्ञात कीजिए।
घंटों में भर सकते हैं। बड़े व्यास वाला नल हौज को भरने में, कम व्यास वाले नल से 10 घंटे कम समय लेता है। प्रत्येक द्वारा अलग से हौज को भरने का समय ज्ञात कीजिए।
- हल:
माना छोटे नल द्वारा लिया गया समय = घंटे
घंटे
बड़े नल द्वारा लिया गया समय =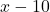 घंटे
घंटे
दोनों द्वारा लिया गया समय =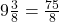 घंटे
घंटे
1 घंटे में छोटे नल का काम =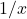
1 घंटे में बड़े नल का काम =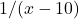
1 घंटे में दोनों का काम =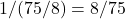
प्रश्नानुसार: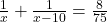
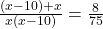
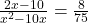
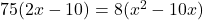
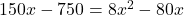
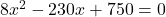
(2 से भाग दें)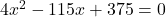
(सूत्र विधि)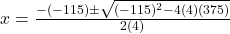
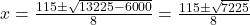
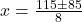
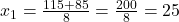
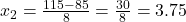 (असंभव, क्योंकि
(असंभव, क्योंकि 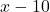 ऋणात्मक हो जाएगा)
ऋणात्मक हो जाएगा)
छोटा नल =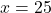 घंटे
घंटे
बड़ा नल =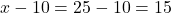 घंटे
घंटे
उत्तर: छोटा नल 25 घंटे, बड़ा नल 15 घंटे।
प्र.36 दो वर्गों के क्षेत्रफलों का योग 468 m² है। यदि उनके परिमापों का अंतर 24 m हो, तो दोनों वर्गों की भुजाएँ ज्ञात कीजिए।
- हल:
माना पहले वर्ग की भुजा = m, दूसरे की =
m, दूसरे की =  m
m
क्षेत्रफलों का योग: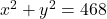 (समीकरण 1)
(समीकरण 1)
परिमापों का अंतर: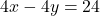 (मान लें
(मान लें 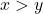 )
) (समीकरण 2)
(समीकरण 2)
(समीकरण 2 का मान 1 में रखने पर)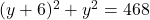
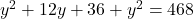
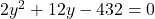
(2 से भाग दें)
(गुणनखंड: योग 6, गुणनफल -216. वो हैं 18 और -12)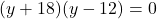
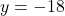 (असंभव) या
(असंभव) या 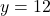
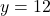 m
m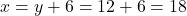 m
m
उत्तर: वर्गों की भुजाएँ 12 m और 18 m हैं।
प्र.37 स्थिति को गणितीय रूप में व्यक्त कीजिए: जॉन और जीवंती दोनों के पास कुल मिलाकर 45 कंचे हैं। दोनों पाँच-पाँच कंचे खो देते हैं और अब उनके पास कंचों की संख्या का गुणनफल 124 है।
- हल:
माना जॉन के पास कंचे =
जीवंती के पास कंचे =
5 कंचे खोने के बाद:
जॉन के पास =
जीवंती के पास =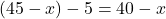
प्रश्नानुसार, गुणनफल 124 है: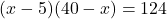
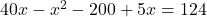
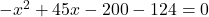
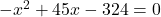
उत्तर (गणितीय रूप):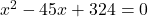
प्र.38 स्थिति को गणितीय रूप में व्यक्त कीजिए: एक आयताकार भूखंड का क्षेत्रफल 528 m² है। क्षेत्र की लम्बाई (मीटरों में) चौड़ाई के दोगुने से एक अधिक है।
- हल:
माना चौड़ाई = m
m
लम्बाई = m
m
क्षेत्रफल =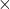
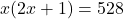
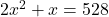
उत्तर (गणितीय रूप):