MP Board 10th Mathematics Quarterly Exam 2025-26 Question Bank : इस MP Board 10th Mathematics Quarterly Exam 2025-26 Question Bank से ब्लूप्रिंट के अनुरूप प्रश्न पत्र के आधार पर छात्र अपनी तैयारी कर सकते हैं ।
त्रैमासिक परीक्षा 2025-26 तृतीय चरण
कक्षा :- 10
विषय :- गणित
पूर्णांक :- 75 समय :- 3:00 घंटे
अध्याय 1: वास्तविक संख्याएँ
1 अंक वाले प्रश्न
प्र. 1. सही विकल्प चुनिये:
- 96 और 404 का HCF होगा : (a) 120 (b) 4 (c) 10 (d) 3
- 12 और 15 का HCF होगा : (a) 3 (b) 4 (c) 10 (d) 5
- दो संख्याओं का गुणनफल = 32 तथा उनका LCM = 8 है तो उनका HCF होगा: (a) 4 (b) 8 (c) 32 (d) 256
- 4 और 7 का महत्तम समापवर्तक (HCF) होगा : (a) 1 (b) 2 (c) 3 (d) 4
- संख्याओं 5, 15, 20 के लिए LCM और HCF का अनुपात होगा: (a) 9:1 (b) 4:3 (c) 11:1 (d) 12:1
- निम्नलिखित में से कौनसी अपरिमेय संख्या है : (a) 2 (b) 3 (c) 5 (d) उपरोक्त सभी
- 12, 15 और 21 का LCM होगा : (a) 180 (b) 315 (c) 420 (d) 252
- यदि दो संख्याओं का गुणनफल 135 तथा उनका HCF 3 हो तो उनका LCM होगा : (a) 45 (b) 315 (c) 420 (d) 135
- 17, 23 और 28 का HCF होगा : (a) 1 (b) 29 (c) 23 (d) 17
- 11 और 13 का HCF होगा : (a) 11 (b) 13 (c) 13 (d) 1
- 8, 9 और 25 का LCM होगा : (a) 72 (b) 225 (c) 1800 (d) 2000
- 5-2 कौनसी संख्या है : (a) परिमेय (b) अपरिमेय (c) परिमेय और अपरिमेय दोनों (d) उपरोक्त में से कोई नहीं
- 15 और 20 का LCM होगा : (a) 60 (b) 300 (c) 30 (d) 90
- प्र. 2. रिक्त स्थान की पूर्ति कीजिये:
- संख्याओं 8, 9 और 25 के HCF का मान __ होगा |
- 2 एक __ संख्या है | (परिमेय / अपरिमेय) |
- 135 और 225 का HCF __ |
- 3
 एक __ संख्या है | (परिमेय / अपरिमेय)
एक __ संख्या है | (परिमेय / अपरिमेय) - यदि a और b दो धनात्मक पूर्णांक हैं तो HCF (a, b) × LCM (a,b) = __
प्र. 3. सत्य / असत्य लिखिए:
- एक प्राकृत संख्या का अभाज्य गुणनखंडन, उसके गुणनखंडों के क्रम को छोड़ते हुए अद्वितीय होता है |
- प्रत्येक अपरिमेय संख्या एक वास्तविक संख्या होती है ।
- प्रत्येक वास्तविक संख्या एक अपरिमेय संख्या होती है ।
- 15 और 21 का LCM 105 है |
- 1/Root 2 एक परिमेय संख्या है |
- दो संख्याओं का गुणनफल उनके HCF और LCM के गुणनफल के बराबर होता है |
- 26 और 91 का HCF 13 होगा |
- यदि p कोई अभाज्य संख्या है और p, a2 को विभाजित करता है तो p, a को भी विभाजित करेगा, जहाँ a एक धनात्मक पूर्णांक है ।
2 अंक वाले प्रश्न
प्र. 6. अंकगणित की आधारभूत प्रमेय लिखिए |
प्र. 7. संख्या 5005 के अभाज्य गुणनखंड लिखिए |
प्र. 8. संख्या 3825 को अभाज्य गुणनखंडों के गुणनफल के रूप में व्यक्त कीजिए |
प्र. 9. संख्या 7429 को अभाज्य गुणनखंडों के गुणनफल के रूप में व्यक्त कीजिए |
प्र. 10. संख्याओं 135 और 225 का HCF ज्ञात कीजिए |
प्र. 11. संख्याओं 9 और 25 का अभाज्य गुणनखंडन विधि से HCF ज्ञात कीजिए |
प्र. 12. संख्याओं 5 और 15 का LCM ज्ञात कीजिए |
प्र. 13. संख्याओं 92 और 510 का HCF ज्ञात कीजिए |
प्र. 14. संख्याओं 867 और 255 का HCF ज्ञात कीजिए |
प्र. 15. संख्याओं 4052 और 12576 का HCF ज्ञात कीजिए |
प्र. 16. HCF (306, 657 ) = 9 दिया है | LCM ( 306, 657 ) ज्ञात कीजिए |
प्र. 17. किसी खेल के मैदान के चारों ओर एक वृत्ताकार पथ है | इस मैदान का एक चक्कर लगाने में सोनिया को 18 मिनट लगते हैं, जबकि इसी मैदान का एक चक्कर लगाने में रवि को 12 मिनट लगते हैं | मान लीजिए वे दोनों एक ही स्थान और एक ही समय पर चलना प्रारंभ करके एक ही दिशा में चलते हैं | कितने समय T बाद वे पुनः प्रारम्भिक स्थान पर मिलेंगे |
प्र. 18. संख्याओं 4n पर विचार कीजिए जहाँ n एक प्राकृत संख्या है | जाँच कीजिए कि क्या n का कोई मान है, जिसके लिए 4n अंक शून्य (0) पर समाप्त होता है |
प्र. 19. संख्याओं 6n पर विचार कीजिए, जहाँ n एक प्राकृत संख्या है | जाँच कीजिए कि क्या n का कोई मान है, जिसके लिए 6n अंक शून्य (0) पर समाप्त होता है |
प्र. 20. व्याख्या कीजिए कि 7×11×13+13 और 7×6×5×4×3×2×1+5 भाज्य संख्याएँ क्यों हैं?
3 अंक वाले प्रश्न प्र.
- प्र. 21. 13, 39 और 52 का HCF और LCM ज्ञात कीजिए |
प्र. 22. संख्या 4, 16 और 20 का HCF और LCM ज्ञात कीजिए |
प्र. 23. सिद्ध कीजिए कि 72 एक अपरिमेय संख्या है |
प्र. 24. सिद्ध कीजिए कि 25 एक अपरिमेय संख्या है |
प्र. 25. दर्शाइए कि 32 एक अपरिमेय संख्या है |
प्र. 26. दर्शाइए कि 5–3 एक अपरिमेय संख्या है ?
प्र. 27. सिद्ध कीजिए कि 3+25 एक अपरिमेय संख्या है |
प्र. 28. संख्याओं 6 और 20 का अभाज्य गुणनखंडन विधि से HCF और LCM ज्ञात कीजिए |
प्र. 29. संख्याओं 6, 72 और 120 का अभाज्य गुणनखंडन विधि से HCF और LCM ज्ञात कीजिए |
प्र. 30. अभाज्य गुणनखंडन विधि द्वारा पूर्णांकों 12, 15 और 21 के HCF और LCM ज्ञात कीजिए |
प्र. 31. अभाज्य गुणनखंडन विधि द्वारा 96 और 404 का HCF ज्ञात कीजिए और फिर इनका LCM ज्ञात कीजिए |
प्र. 32. संख्याओं 17, 23 और 29 का अभाज्य गुणनखंडन विधि से HCF और LCM ज्ञात कीजिए |
प्र. 33. संख्याओं 26 और 91 के HCF और LCM ज्ञात कीजिए तथा जाँच कीजिए कि दो संख्याओं का गुणनफल = HCF X LCM.
प्र. 34. संख्याओं 510 और 92 के HCF और LCM ज्ञात कीजिए तथा जाँच कीजिए कि दो संख्याओं का गुणनफल = HCF X LCM
प्र. 35. सिद्ध कीजिए कि 2 एक अपरिमेय संख्या है |
अध्याय 2: बहुपद
1 अंक वाले प्रश्न
प्र.1. सही विकल्प चुनिये:
- यदि द्विघात बहुपद
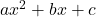 के शून्यक
के शून्यक  और
और  हों, तो
हों, तो  का मान होगा:
का मान होगा: - यदि द्विघात बहुपद
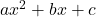 के शून्यक
के शून्यक  और
और  हों, तो
हों, तो  का मान होगा:
का मान होगा: - रेखीय बहुपद
 का शून्यक होगा:
का शून्यक होगा: - बहुपद
 के शून्यक होंगे:
के शून्यक होंगे: - बहुपद
 के शून्यक होंगे:
के शून्यक होंगे: - बहुपद
 के लिए घात होगी:
के लिए घात होगी: - यदि द्विघात बहुपद के शून्यक
 तथा
तथा 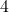 हों तो द्विघात बहुपद होगा:
हों तो द्विघात बहुपद होगा: - किसी बहुपद
 के कुल शून्यक, उस बहुपद के आरेख के निम्नलिखित पर प्रतिच्छेदन के कुल बिन्दुओं की संख्या के बराबर होते हैं:
के कुल शून्यक, उस बहुपद के आरेख के निम्नलिखित पर प्रतिच्छेदन के कुल बिन्दुओं की संख्या के बराबर होते हैं: - बहुपद
 की घात होगी:
की घात होगी: - बहुपद
 के शून्यकों का गुणनफल होगा:
के शून्यकों का गुणनफल होगा: - बहुपद
 के शून्यकों का योग होगा:
के शून्यकों का योग होगा: - निम्नलिखित में से कौनसा बहुपद नहीं है:
(a) ![]() (b)
(b) ![]() (c)
(c) ![]() (d)
(d) ![]()
(a) ![]() (b)
(b) ![]() (c)
(c) ![]() (d)
(d) ![]()
(a) ![]() (b)
(b) ![]() (c)
(c) ![]() (d)
(d) ![]()
(a) ![]() (b)
(b) ![]() (c)
(c) ![]() (d)
(d) ![]()
(a) ![]() (b)
(b) ![]() (c)
(c) ![]() (d)
(d) ![]()
(a) ![]() (b)
(b) ![]() (c)
(c) ![]() (d)
(d) ![]()
(a) ![]() (b)
(b) ![]() (c)
(c) ![]() (d)
(d) ![]()
(a) ![]() अक्ष पर
(b)
अक्ष पर
(b) ![]() अक्ष पर
(c)
अक्ष पर
(c) ![]() अक्ष तथा
अक्ष तथा ![]() अक्ष दोनों पर
(d) इनमें से कोई नहीं
अक्ष दोनों पर
(d) इनमें से कोई नहीं
(a) ![]() (b)
(b) ![]() (c)
(c) ![]() (d)
(d) ![]()
(a) ![]() (b)
(b) ![]() (c)
(c) ![]() (d)
(d) ![]()
(a) ![]() (b)
(b) ![]() (c)
(c) ![]() (d)
(d) ![]()
(a) ![]() (b)
(b) ![]() (c)
(c) ![]() (d)
(d) ![]()
प्र.2. रिक्त स्थान की पूर्ति कीजिये:
- रेखीय बहुपद
 का शून्यक \_________\_ है |
का शून्यक \_________\_ है | - दो बहुपदों का गुणनफल एक \_________\_ होता है |
- बहुपद
 के शून्यकों का योग \_________\_ है |
के शून्यकों का योग \_________\_ है | - बहुपद
 के शून्यकों का गुणनफल \_________\_ है |
के शून्यकों का गुणनफल \_________\_ है | - यदि बहुपद
 का एक शून्यक
का एक शून्यक  हो, तब
हो, तब  का मान \_________\_ होगा |
का मान \_________\_ होगा | - घात एक वाले बहुपद \_________\_ बहुपद कहलाते हैं |
- द्विघात बहुपद में शून्यकों की अधिकतम संख्या \_________\_ होती है |
- बहुपद
 की घात \_________\_ है |
की घात \_________\_ है | - यदि
 और
और  बहुपद
बहुपद  के शून्यक हैं तो
के शून्यक हैं तो  का मान \_________\_ होगा |
का मान \_________\_ होगा |
प्र.3. सत्य / असत्य लिखिए:
- एक वास्तविक संख्या
 बहुपद
बहुपद  का शून्यक है, यदि
का शून्यक है, यदि  है |
है | - एक रैखिक बहुपद
 ,
,  के रूप का होता है |
के रूप का होता है |  का ग्राफ
का ग्राफ  -अक्ष को बिंदु
-अक्ष को बिंदु  पर प्रतिच्छेद करता है |
पर प्रतिच्छेद करता है |- बहुपद
 का शून्यक उस बिंदु का
का शून्यक उस बिंदु का  -निर्देशांक है, जहाँ
-निर्देशांक है, जहाँ  का ग्राफ
का ग्राफ  -अक्ष को प्रतिच्छेद करता है |
-अक्ष को प्रतिच्छेद करता है | - एक रैखिक बहुपद
 के लिए,
के लिए,  का ग्राफ एक सरल रेखा है, जो
का ग्राफ एक सरल रेखा है, जो  -अक्ष को ठीक एक बिंदु
-अक्ष को ठीक एक बिंदु  पर प्रतिच्छेद करती है |
पर प्रतिच्छेद करती है | - द्विघात बहुपद
 के शून्यक उन बिन्दुओं के
के शून्यक उन बिन्दुओं के  -निर्देशांक हैं, जहाँ
-निर्देशांक हैं, जहाँ 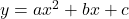 का ग्राफ
का ग्राफ  -अक्ष को प्रतिच्छेद करता है |
-अक्ष को प्रतिच्छेद करता है | - घात
 के लिए दिए गए बहुपद
के लिए दिए गए बहुपद  के लिए,
के लिए,  का ग्राफ
का ग्राफ  -अक्ष को अधिक से अधिक
-अक्ष को अधिक से अधिक  बिन्दुओं पर प्रतिच्छेद करता है |
बिन्दुओं पर प्रतिच्छेद करता है |  घात वाले बहुपद के अधिकतम
घात वाले बहुपद के अधिकतम  शून्यक हो सकते हैं |
शून्यक हो सकते हैं |- द्विघात बहुपद के अधिक से अधिक दो शून्यक हो सकते हैं |
- यदि
 और
और  बहुपद
बहुपद 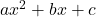 के शून्यक हैं तो
के शून्यक हैं तो  होता है |
होता है |
प्र.4. सही जोड़ी मिलाइए:
| स्तम्भ – A | स्तम्भ – B |
|---|---|
| 1. द्विघात बहुपद |
(i). |
| 2. बहुपद |
(ii). |
| 3. त्रिघात बहुपद है: | (iii). |
| 4. रेखीय बहुपद है: | (iv). |
| 5. द्विघात बहुपद |
(v). |
प्र.5. एक शब्द / वाक्य में उत्तर दीजिये:
- रैखिक बहुपद की घात कितनी होती है?
- द्विघात बहुपद की घात कितनी होती है?
- त्रिघात बहुपद की घात कितनी होती है?
- किसी बहुपद
 के लिए,
के लिए,  का ग्राफ नीचे आकृति में दिया है |
का ग्राफ नीचे आकृति में दिया है |  के शून्यकों की संख्या लिखिए |
के शून्यकों की संख्या लिखिए |
- उन बिन्दुओं के निर्देशांक लिखिए, जहाँ द्विघात बहुपद
 का ग्राफ
का ग्राफ  -अक्ष को प्रतिच्छेद करता है |
-अक्ष को प्रतिच्छेद करता है | - घात
 के किसी बहुपद के अधिक से अधिक
के किसी बहुपद के अधिक से अधिक  शून्यक हो सकते हैं |
शून्यक हो सकते हैं |
2 अंक वाले प्रश्न
 के शून्यक ज्ञात कीजिए |
के शून्यक ज्ञात कीजिए |- बहुपद
 के शून्यक ज्ञात कीजिए |
के शून्यक ज्ञात कीजिए | - बहुपद
 के शून्यक ज्ञात कीजिए |
के शून्यक ज्ञात कीजिए | - यदि बहुपद के शून्यकों का योग
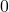 एवं गुणनफल भी
एवं गुणनफल भी  है तो बहुपद ज्ञात कीजिए |
है तो बहुपद ज्ञात कीजिए | - एक द्विघात बहुपद ज्ञात कीजिए, जिसके शून्यकों के योग तथा गुणनफल क्रमशः
 और
और 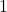 हैं |
हैं | - एक द्विघात बहुपद ज्ञात कीजिए, जिसके शून्यकों के योग तथा गुणनफल क्रमशः
 और
और 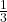 हैं |
हैं | - एक द्विघात बहुपद ज्ञात कीजिए, जिसके शून्यकों के योग तथा गुणनफल क्रमशः
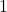 और
और 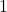 हैं |
हैं | - एक द्विघात बहुपद ज्ञात कीजिए, जिसके शून्यकों के योग तथा गुणनफल क्रमशः
 और
और  हैं |
हैं | - एक द्विघात बहुपद ज्ञात कीजिए, जिसके शून्यकों के योग तथा गुणनफल क्रमशः
 और
और 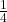 हैं |
हैं | - एक द्विघात बहुपद ज्ञात कीजिए, जिसके शून्यकों के योग तथा गुणनफल क्रमशः
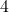 और
और 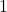 हैं |
हैं |
3 अंक वाले प्रश्न
- बहुपद
 के शून्यक ज्ञात कीजिए और शून्यकों तथा गुणांकों के बीच संबंध की सत्यता की जाँच कीजिए |
के शून्यक ज्ञात कीजिए और शून्यकों तथा गुणांकों के बीच संबंध की सत्यता की जाँच कीजिए | - द्विघात बहुपद
 के शून्यक ज्ञात कीजिए और शून्यकों तथा गुणांकों के बीच संबंध की सत्यता की जाँच कीजिए |
के शून्यक ज्ञात कीजिए और शून्यकों तथा गुणांकों के बीच संबंध की सत्यता की जाँच कीजिए | - बहुपद
 के शून्यक ज्ञात कीजिए और शून्यकों तथा गुणांकों के बीच संबंध की सत्यता की जाँच कीजिए |
के शून्यक ज्ञात कीजिए और शून्यकों तथा गुणांकों के बीच संबंध की सत्यता की जाँच कीजिए | - बहुपद
 के शून्यक ज्ञात कीजिए और शून्यकों तथा गुणांकों के बीच संबंध की सत्यता की जाँच कीजिए |
के शून्यक ज्ञात कीजिए और शून्यकों तथा गुणांकों के बीच संबंध की सत्यता की जाँच कीजिए | - द्विघात बहुपद
 के शून्यक ज्ञात कीजिए और शून्यकों तथा गुणांकों के बीच संबंध की सत्यता की जाँच कीजिए |
के शून्यक ज्ञात कीजिए और शून्यकों तथा गुणांकों के बीच संबंध की सत्यता की जाँच कीजिए | - द्विघात बहुपद
 के शून्यक ज्ञात कीजिए और शून्यकों तथा गुणांकों के बीच संबंध की सत्यता की जाँच कीजिए |
के शून्यक ज्ञात कीजिए और शून्यकों तथा गुणांकों के बीच संबंध की सत्यता की जाँच कीजिए | - द्विघात बहुपद
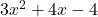 के शून्यक ज्ञात कीजिए और शून्यकों तथा गुणांकों के बीच संबंध की सत्यता की जाँच कीजिए |
के शून्यक ज्ञात कीजिए और शून्यकों तथा गुणांकों के बीच संबंध की सत्यता की जाँच कीजिए | - द्विघात बहुपद
 के शून्यक ज्ञात कीजिए और शून्यकों तथा गुणांकों के बीच संबंध की सत्यता की जाँच कीजिए |
के शून्यक ज्ञात कीजिए और शून्यकों तथा गुणांकों के बीच संबंध की सत्यता की जाँच कीजिए |
अध्याय 3: दो चर वाले रैखिक समीकरण युग्म
1 अंक वाले प्रश्न
प्र.1. सही विकल्प चुनिये:
- निम्नलिखित में से दो चरों में रैखिक समीकरण है:
- यदि
 तो रैखिक समीकरण युग्म
तो रैखिक समीकरण युग्म  तथा
तथा  का
का - यदि
 तो रैखिक समीकरण युग्म
तो रैखिक समीकरण युग्म  तथा
तथा  का
का - यदि
 तो रैखिक समीकरण युग्म
तो रैखिक समीकरण युग्म  तथा
तथा  का
का - रैखिक समीकरण युग्म
 तथा
तथा  का एक अद्वितीय हल होने की शर्त है:
का एक अद्वितीय हल होने की शर्त है: - रैखिक समीकरण युग्म
 तथा
तथा  का कोई हल नहीं होने की शर्त है:
का कोई हल नहीं होने की शर्त है: - रैखिक समीकरण युग्म
 तथा
तथा  के अनन्त अनेक हल होने की शर्त है:
के अनन्त अनेक हल होने की शर्त है:
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
(A) एक अद्वितीय हल होगा | (B) कोई हल नहीं होगा | (C) अनन्ततः अनेक हल होंगे | (D) इनमें से कोई नहीं |
(A) एक अद्वितीय हल होगा | (B) कोई हल नहीं होगा | (C) अनन्ततः अनेक हल होंगे | (D) इनमें से कोई नहीं |
(A) एक अद्वितीय हल होगा | (B) कोई हल नहीं होगा | (C) अनन्ततः अनेक हल होंगे | (D) इनमें से कोई नहीं |
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D) इनमें से कोई नहीं |
(D) इनमें से कोई नहीं |
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D) इनमें से कोई नहीं |
(D) इनमें से कोई नहीं |
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D) इनमें से कोई नहीं |
(D) इनमें से कोई नहीं |
प्र.2. रिक्त स्थान की पूर्ति कीजिये:
- समीकरण
 में यदि
में यदि 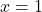 तो
तो  के रूप में रखा जा सकता है, जहाँ
के रूप में रखा जा सकता है, जहाँ  और
और  वास्तविक संख्याएँ हैं और
वास्तविक संख्याएँ हैं और  और
और  दोनों शून्य नहीं हैं, दो चरों
दोनों शून्य नहीं हैं, दो चरों  और
और  में एक __________ कहलाता है |
में एक __________ कहलाता है | - समीकरण
 में यदि
में यदि  हो तो
हो तो  का मान __________ होगा |
का मान __________ होगा |
प्र.3 सत्य / असत्य लिखिए:
- दो चरों में एक रैखिक समीकरण के अनेक हल होते हैं |
- रैखिक समीकरण का प्रत्येक हल उसको निरूपित करने वाली रेखा पर स्थित एक बिंदु होता है |
- समीकरण निकाय
 एवं
एवं  द्वारा निरूपित रेखाएँ प्रतिच्छेदी होंगी |
द्वारा निरूपित रेखाएँ प्रतिच्छेदी होंगी |
प्र.4. सही जोड़ी मिलाइए:
| स्तम्भ – अ | स्तम्भ – ब |
|---|---|
| 1. |
(i). |
| 2. दो चरों में रैखिक समीकरण का व्यापक रूप | (ii). |
| 3. |
(iii). |
| 4. |
(iv). |
| 5. |
(v). निकाय द्वारा निरूपित रेखाएँ संपाती |
प्र.5 एक शब्द/वाक्य में उत्तर दीजिए |
- दो चरों में रैखिक समीकरण का मानक रूप लिखिए |
- रैखिक समीकरण
 में यदि
में यदि  हो तो
हो तो  का क्या मान होगा ?
का क्या मान होगा ? - यदि दो संतरों और पांच सेबों का मूल्य Rs. 70 है, तो इस स्थिति को रैखिक समीकरण के रूप में प्रदर्शित कीजिए |
2 अंक वाले प्रश्न
- कक्षा X के 10 विद्यार्थियों ने एक गणित की पहेली प्रतियोगिता में भाग लिया | लड़कियों की संख्या लड़कों की संख्या से 4 अधिक है | इस स्थिति के लिए रैखिक समीकरण बनाइए |
- एक आयताकार बाग, जिसकी लम्बाई, चौड़ाई से 4 मी. अधिक है, का अर्द्ध-परिमाप 36 मी. है | इस स्थिति को रैखिक समीकरण युग्म के रूप में प्रदर्शित कीजिए |
- अनुपातों
 ,
, 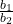 और
और 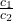 की तुलना कर ज्ञात कीजिए कि समीकरण युग्म
की तुलना कर ज्ञात कीजिए कि समीकरण युग्म  और
और  द्वारा निरूपित रेखाएँ एक बिंदु पर प्रतिच्छेद करती हैं, समांतर हैं अथवा संपाती हैं |
द्वारा निरूपित रेखाएँ एक बिंदु पर प्रतिच्छेद करती हैं, समांतर हैं अथवा संपाती हैं | - अनुपातों
 ,
, 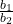 और
और 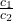 की तुलना कर ज्ञात कीजिए कि समीकरण युग्म
की तुलना कर ज्ञात कीजिए कि समीकरण युग्म  और
और  द्वारा निरूपित रेखाएँ एक बिंदु पर प्रतिच्छेद करती हैं, समांतर हैं अथवा संपाती हैं |
द्वारा निरूपित रेखाएँ एक बिंदु पर प्रतिच्छेद करती हैं, समांतर हैं अथवा संपाती हैं | - अनुपातों
 ,
, 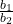 और
और 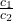 की तुलना कर ज्ञात कीजिए कि समीकरण युग्म
की तुलना कर ज्ञात कीजिए कि समीकरण युग्म  और
और  संगत है या असंगत |
संगत है या असंगत | - अनुपातों
 ,
, 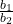 और
और 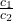 की तुलना कर ज्ञात कीजिए कि समीकरण युग्म
की तुलना कर ज्ञात कीजिए कि समीकरण युग्म  और
और  संगत है या असंगत |
संगत है या असंगत |
4 अंक वाले प्रश्न
- रैखिक समीकरण युग्म
![Rendered by QuickLaTeX.com \[ 3x + 5y - 8 = 0 \]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-c1060f13b2f34408984ae19c4fe2d379_l3.png)
को विलोपन विधि से हल कीजिए |![Rendered by QuickLaTeX.com \[ 9x = 2y + 7 \]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-689fdc24c9bb1366f47d30360a8a0bba_l3.png)
- समीकरण युग्म
 ,
,  को प्रतिस्थापन विधि से हल कीजिए |
को प्रतिस्थापन विधि से हल कीजिए |
- निम्न रैखिक समीकरण युग्म को प्रतिस्थापन विधि से हल कीजिए:
![Rendered by QuickLaTeX.com \[ 3x + 4y = 10 \]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-a744629c872b75b15bd9f0be06b64e69_l3.png)
![Rendered by QuickLaTeX.com \[ 2x - 2y = 2 \]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-3c92a38523e1898237f8d02e87a92e56_l3.png)
- दो व्यक्तियों की आय का अनुपात
 है और उनके खर्चों का अनुपात
है और उनके खर्चों का अनुपात  है | यदि प्रत्येक व्यक्ति महीने में ₹ 2000 बचा लेता है, तो उनकी मासिक आय ज्ञात कीजिए |
है | यदि प्रत्येक व्यक्ति महीने में ₹ 2000 बचा लेता है, तो उनकी मासिक आय ज्ञात कीजिए |
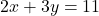 और
और  को हल कीजिए और इसमें
को हल कीजिए और इसमें  का वह मान ज्ञात कीजिए जिसके लिए
का वह मान ज्ञात कीजिए जिसके लिए  |
|
- दो संपूरक कोणों में बड़ा कोण छोटे कोण से 18 डिग्री अधिक है | उन्हें ज्ञात कीजिए |
- एक क्रिकेट टीम के कोच ने 7 बल्ले तथा 6 गेंदें ₹3800 में खरीदीं | बाद में उसने 3 बल्ले तथा 5 गेंदें ₹1750 में खरीदीं | प्रत्येक बल्ले और प्रत्येक गेंद का मूल्य ज्ञात कीजिए |
- दो अंकों की एक संख्या एवं उसके अंकों को उलटने पर बनी संख्या का योग 66 है | यदि संख्या के अंकों का अंतर 2 हो, तो संख्या ज्ञात कीजिए | ऐसी संख्याएँ कितनी हैं?
- 5 पेंसिल तथा 7 कलमों का कुल मूल्य Rs. 50 है, जबकि 7 पेंसिल तथा 5 कलमों का कुल मूल्य Rs. 46 है | एक पेंसिल का मूल्य तथा एक कलम का मूल्य ज्ञात कीजिए |
- दो संख्याओं का अंतर 26 है और एक संख्या दूसरी संख्या की तीन गुनी है | उन्हें ज्ञात कीजिए |
- एक भिन्न
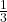 हो जाती है जब उसके अंश से एक घटाया जाय और वह
हो जाती है जब उसके अंश से एक घटाया जाय और वह 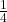 हो जाती है जब हर में 8 जोड़ दिया जाता है | वह भिन्न ज्ञात करें |
हो जाती है जब हर में 8 जोड़ दिया जाता है | वह भिन्न ज्ञात करें |
- विलोपन विधि से हल करें –
![Rendered by QuickLaTeX.com \[ \frac{x}{2} + \frac{2y}{3} = -1 \]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-192a99105bf51f2a0a1061b821d48c5e_l3.png)
![Rendered by QuickLaTeX.com \[ x - \frac{y}{3} = 3 \]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-e3fbcd53c4865e8de1b59d97d262bf4c_l3.png)
- प्रतिस्थापन विधि से हल करें –
![Rendered by QuickLaTeX.com \[ 0.2x + 0.3y = 1.3 \]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-d5012cab194a4eeb4427053a279bb733_l3.png)
![Rendered by QuickLaTeX.com \[ 0.4x + 0.5y = 2.3 \]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-d9ba743bc91471015faa0a6f679e6d2f_l3.png)
- 5 पेंसिल तथा 7 कलमों का कुल मूल्य ₹ 50 है, जबकि 7 पेंसिल तथा 5 कलमों का कुल मूल्य ₹ 46 है | एक पेंसिल का मूल्य तथा एक कलम का मूल्य ज्ञात कीजिए | इस समस्या के लिए रैखिक समीकरण के युग्म बनाइए और ग्राफीय विधि से हल कीजिए |
- निम्न समस्या में रैखिक समीकरणों का युग्म बनाइए और ग्राफीय विधि से हल कीजिए: कक्षा X के 10 विद्यार्थियों ने एक गणित की पहेली प्रतियोगिता में भाग लिया | लड़कियों की संख्या लड़कों की संख्या से 4 अधिक है |
- ग्राफ द्वारा जाँच कीजिए कि समीकरण युग्म
 और
और  संगत है | यदि ऐसा है, तो उन्हें ग्राफीय विधि द्वारा हल कीजिए |
संगत है | यदि ऐसा है, तो उन्हें ग्राफीय विधि द्वारा हल कीजिए |
- एक आयताकार बाग, जिसकी लम्बाई, चौड़ाई से 4 मी. अधिक है, का अर्द्ध-परिमाप 36 मी. है | बाग की विमाएँ ज्ञात कीजिए |
अध्याय 4: द्विघात समीकरण
1 अंक वाले प्रश्न
प्र.1. सही विकल्प चुनिये:
- यदि द्विघात समीकरण
 के मूल समान हों तो समीकरण के विविक्तकर का मान होगा:
के मूल समान हों तो समीकरण के विविक्तकर का मान होगा: - समीकरण
 के मूलों की प्रकृति होगी:
के मूलों की प्रकृति होगी: - किसी द्विघात समीकरण में चर कि अधिकतम घात होती है:
- द्विघात समीकरण
 का विविक्तकर होगा:
का विविक्तकर होगा: - निम्नलिखित में से किस द्विघात समीकरण के मूल वास्तविक होंगे:
- द्विघात समीकरण
 के मूल होंगे:
के मूल होंगे: - निम्न में कौन एक वर्ग समीकरण नहीं हैं?
- यदि
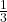 वर्ग समीकरण
वर्ग समीकरण  का एक मूल है, तो
का एक मूल है, तो  का मान होगा:
का मान होगा:  के किस मान के लिये वर्ग समीकरण
के किस मान के लिये वर्ग समीकरण  के दोनों मूल बराबर होंगे:
के दोनों मूल बराबर होंगे:- द्विघात समीकरण
 के विविक्तकर का मान होगा:
के विविक्तकर का मान होगा: - द्विघात समीकरण
 के मूल होंगे:
के मूल होंगे: - द्विघात समीकरण में मूलों की अधिकतम संख्या होती है:
- समीकरण
 के हल है:
के हल है: - वर्ग समीकरण
 के मूलों की प्रकृति है:
के मूलों की प्रकृति है:  के मूल हैं:
के मूल हैं:- जब वर्ग समीकरण
 के मूल समान हों तब:
के मूल समान हों तब:
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
(A) वास्तविक और समान (B) वास्तविक और भिन्न (C) कोई वास्तविक मूल नहीं (D) इनमें से कोई नहीं
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
(A) ![]() और
और ![]() (B)
(B) ![]() और
और ![]() (C)
(C) ![]() और
और ![]() (D)
(D) ![]() और
और ![]()
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
(A) वास्तविक (B) काल्पनिक (C) वास्तविक और काल्पनिक दोनों (D) इनमें से कोई नहीं
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
(A) वास्तविक एवं भिन्न (B) वास्तविक एवं समान (C) काल्पनिक (D) इनमें से कोई नहीं
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
प्र.2. रिक्त स्थान की पूर्ति कीजिए |
- एक समीकरण
 , जहाँ
, जहाँ  घात
घात  का बहुपद हो, \_________\_ समीकरण कहलाती है |
का बहुपद हो, \_________\_ समीकरण कहलाती है | - किसी द्विघात समीकरण के अधिकतम __________ मूल होते हैं |
- समीकरण
 के मूल __________ हैं |
के मूल __________ हैं | - यदि किसी द्विघात समीकरण के मूल वास्तविक और समान हों तो उस समीकरण के विविक्तकर का मान __________ होगा |
- द्विघात समीकरण से मूल ज्ञात करने का सूत्र प्राचीन भारतीय गणितज्ञ __________ ने दिया था |
- द्विघात समीकरण का विविक्तकर ऋणात्मक हो, तो मूल __________ होंगे |
- वर्ग समीकरण
 के मूल __________ होंगे |
के मूल __________ होंगे | - यदि
 एक द्विघात बहुपद है, तो
एक द्विघात बहुपद है, तो  को __________ कहते हैं |
को __________ कहते हैं | - द्विघात समीकरण
 के मूल ज्ञात करने हेतु सूत्र है:
के मूल ज्ञात करने हेतु सूत्र है:  |
| - यदि
 हो, तो द्विघात समीकरण
हो, तो द्विघात समीकरण  के दोनों मूल __________ होते हैं |
के दोनों मूल __________ होते हैं | - द्विघात समीकरण
 के मूलों की प्रकृति __________ होगी |
के मूलों की प्रकृति __________ होगी |
प्र.3 सत्य / असत्य लिखिए |
- एक द्विघात समीकरण के एक से अधिक मूल हो सकते हैं |
- समीकरण
 के मूल
के मूल 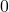 और
और  होंगे |
होंगे | - समीकरण
 के मूल समान होंगे |
के मूल समान होंगे |  एक द्विघात समीकरण है |
एक द्विघात समीकरण है |- वर्ग समीकरण में चर की अधिकतम घात कुछ भी हो सकती है |
 में
में  के मान
के मान 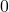 और
और 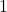 हैं |
हैं |- जब वर्ग समीकरण के दोनों मूल समान हों तब विविक्तकर
 होता है |
होता है | - वर्ग समीकरण
 के मूलों का योगफल
के मूलों का योगफल  है |
है | - वर्ग समीकरण के अनेक हल होते हैं |
- जब
 तो वर्ग समीकरण के मूल वास्तविक होते हैं |
तो वर्ग समीकरण के मूल वास्तविक होते हैं |
प्र.4. सही जोड़ी बनाइए |
| स्तम्भ – A | स्तम्भ – B |
|---|---|
| (i) यदि किसी द्विघात समीकरण का विविक्तकर |
(अ) |
| (ii) यदि |
(ब) तो मूल वास्तविक तथा भिन्न |
| (iii) द्विघात समीकरण |
(स) |
| (iv) द्विघात समीकरण |
(द) |
| (v) द्विघात समीकरण |
(ई) |
प्र.5 एक शब्द / वाक्य में उत्तर दीजिए |
- समीकरण
 में
में  क्या कहलाता है?
क्या कहलाता है? - यदि किसी द्विघात समीकरण के मूल वास्तविक एवं समान हों तो उस समीकरण के विविक्तकर का मान कितना होगा?
- यदि किसी द्विघात समीकरण के विविक्तकर का मान ऋणात्मक हो तो उस समीकरण के मूलों की प्रकृति कैसी होगी?
- यदि किसी द्विघात समीकरण के विविक्तकर का मान धनात्मक हो तो उस समीकरण के मूलों की प्रकृति कैसी होगी?
- द्विघात समीकरण का मानक रूप लिखिए?
- द्विघात समीकरण
 का विविक्तकर ज्ञात करने का सूत्र लिखिए?
का विविक्तकर ज्ञात करने का सूत्र लिखिए? - यदि किसी वर्ग समीकरण का विविक्तकर धनात्मक पूर्ण संख्या हो तो उसके मूल कैसे होंगे?
- वर्ग समीकरण
 के मूलों का योगफल क्या होगा?
के मूलों का योगफल क्या होगा? - वर्ग समीकरण
 के मूलों का गुणनफल क्या होगा?
के मूलों का गुणनफल क्या होगा? - समीकरण जिसमें चर की अधिकतम घात दो हो तो क्या कहलाता है?
- क्या
 एक द्विघात समीकरण है?
एक द्विघात समीकरण है? - द्विघात समीकरण
 के मूल क्या होंगे?
के मूल क्या होंगे? - वर्ग समीकरण
 के मूलों का योग कितना होगा?
के मूलों का योग कितना होगा?
2 अंक वाले प्रश्न
- निम्नलिखित स्थिति को गणितीय रूप में व्यक्त कीजिए:
एक रेलगाड़ी
 km की दूरी समान चाल से तय करती है | यदि इसकी चाल
km की दूरी समान चाल से तय करती है | यदि इसकी चाल  km/h कम होती तो वह उसी दूरी को तय करने में
km/h कम होती तो वह उसी दूरी को तय करने में 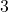 घंटे अधिक लेती | हमें रेलगाड़ी की चाल ज्ञात करनी है |
घंटे अधिक लेती | हमें रेलगाड़ी की चाल ज्ञात करनी है | - निम्नलिखित स्थिति को गणितीय रूप में व्यक्त कीजिए:
दो क्रमागत धनात्मक पूर्णांकों का गुणनफल
 है | हमें पूर्णांकों को ज्ञात करना है |
है | हमें पूर्णांकों को ज्ञात करना है | - निम्न स्थिति को गणितीय रूप में व्यक्त कीजिए:
एक आयताकार भूखंड का क्षेत्रफल
 है | क्षेत्र की लम्बाई (मीटरों में) चौड़ाई के दुगुने से एक अधिक है | हमें भूखंड की लम्बाई और चौड़ाई ज्ञात करनी है |
है | क्षेत्र की लम्बाई (मीटरों में) चौड़ाई के दुगुने से एक अधिक है | हमें भूखंड की लम्बाई और चौड़ाई ज्ञात करनी है | - जाँच कीजिए कि समीकरण
 द्विघात समीकरण हैं या नहीं |
द्विघात समीकरण हैं या नहीं | - जाँच कीजिए कि समीकरण
 द्विघात समीकरण हैं या नहीं |
द्विघात समीकरण हैं या नहीं | - जाँच कीजिए कि समीकरण
 द्विघात समीकरण हैं या नहीं |
द्विघात समीकरण हैं या नहीं | - द्विघात समीकरण
 मूलों की प्रकृति ज्ञात कीजिए |
मूलों की प्रकृति ज्ञात कीजिए |
4 अंक वाले प्रश्न
- गुणनखंड विधि से समीकरण
 को हल कीजिए |
को हल कीजिए | - गुणनखंड विधि से समीकरण
 को हल कीजिए |
को हल कीजिए | - गुणनखंड विधि से समीकरण
 को हल कीजिए |
को हल कीजिए | - गुणनखंड विधि से समीकरण
 को हल कीजिए |
को हल कीजिए | - द्विघात समीकरण
 के मूल ज्ञात कीजिए |
के मूल ज्ञात कीजिए | - वर्ग समीकरण
 के मूल ज्ञात कीजिए |
के मूल ज्ञात कीजिए | - द्विघात समीकरण
 में
में  का ऐसा मान ज्ञात कीजिए जिससे समीकरण के दो बराबर मूल हों |
का ऐसा मान ज्ञात कीजिए जिससे समीकरण के दो बराबर मूल हों | - द्विघात समीकरण
 में
में  का ऐसा मान ज्ञात कीजिए जिससे समीकरण के दो बराबर मूल हों |
का ऐसा मान ज्ञात कीजिए जिससे समीकरण के दो बराबर मूल हों | - दो संख्याएँ ज्ञात कीजिए जिनका योग
 तथा गुणनफल
तथा गुणनफल  हो |
हो | - दो क्रमागत धनात्मक पूर्णांक ज्ञात कीजिए जिनके वर्गों का योग
 है |
है | - दो ऐसे क्रमागत सम पूर्णांक ज्ञात कीजिए जिनके वर्गों का योग
 हो |
हो | - एक समकोण त्रिभुज की ऊँचाई उसके आधार से
 सेमी कम है | यदि कर्ण
सेमी कम है | यदि कर्ण  सेमी का हो तो अन्य दो भुजाएँ ज्ञात कीजिए?
सेमी का हो तो अन्य दो भुजाएँ ज्ञात कीजिए? - दो ऐसे क्रमागत विषम धनात्मक पूर्णांक ज्ञात कीजिए जिनके वर्गों का योग
 हो |
हो |
अध्याय 5: समांतर श्रेणियाँ
1 अंक वाले प्रश्न
प्र.1. सही विकल्प चुनिये:
- A.P.:
 के लिए प्रथम पद एवं सार्व-अंतर क्रमशः हैं:
के लिए प्रथम पद एवं सार्व-अंतर क्रमशः हैं: - A.P.:
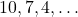 का 30 वां पद है:
का 30 वां पद है: - A.P.:
 का 11 वां पद है:
का 11 वां पद है:  का कौनसा पद
का कौनसा पद 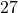 है:
है: का 11 वां पद है:
का 11 वां पद है:- समांतर श्रेणी
 का सार्व-अंतर है –
का सार्व-अंतर है – - समांतर श्रेणी
 का 5वां पद है:
का 5वां पद है: - किसी श्रेणी का प्रथम पद
 तथा सार्व-अंतर
तथा सार्व-अंतर 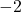 हो तो प्रथम चार पद होंगे –
हो तो प्रथम चार पद होंगे – - समांतर श्रेणी में
 तब
तब  है:
है: - श्रेणी
 का प्रथम पद एवं सार्व-अंतर है
का प्रथम पद एवं सार्व-अंतर है - 3 के गुणज प्रथम पांच पदों का योगफल है:
- समांतर श्रेणी
 का 10 वां पद:
का 10 वां पद: - समांतर श्रेणी का सार्व-अंतर ज्ञात कीजिए जबकि
 हो:
हो:
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
(A) पाँचवाँ (B) आठवाँ (C) नववाँ (D) छठवाँ
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
(A) ![]() और
और ![]() (B)
(B) ![]() और
और ![]() (C)
(C) ![]() और
और ![]() (D)
(D) ![]() और
और ![]()
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
प्र.2. रिक्त स्थान की पूर्ति कीजिए |
- समांतर श्रेणी
 में सार्वअंतर \_________\_ है |
में सार्वअंतर \_________\_ है | - यदि किसी समांतर श्रेणी का
 वां पद
वां पद 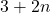 हो तो श्रेणी का प्रथम पद __________ होगा |
हो तो श्रेणी का प्रथम पद __________ होगा | - समांतर श्रेणी का प्रथम पद
 तथा सार्व-अंतर
तथा सार्व-अंतर  हो तो उसका दसवाँ पद __________ होगा |
हो तो उसका दसवाँ पद __________ होगा | - यदि
 समांतर श्रेणी में हैं, तब
समांतर श्रेणी में हैं, तब  को
को  और
और  का __________ कहते हैं |
का __________ कहते हैं |  पदों वाली समांतर श्रेणी का प्रथम पद
पदों वाली समांतर श्रेणी का प्रथम पद  तथा अंतिम पद
तथा अंतिम पद  हो, तो श्रेणी का योगफल __________ होता है |
हो, तो श्रेणी का योगफल __________ होता है |- समांतर श्रेणी के कोई दो लगातार पदों का अन्तर __________ कहलाता है |
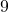 और
और  का समांतर माध्य __________ होता है |
का समांतर माध्य __________ होता है |- समांतर श्रेणी
 का सार्व-अंतर __________ है |
का सार्व-अंतर __________ है | - श्रेणी
 का 8वां पद __________ है |
का 8वां पद __________ है | - समांतर श्रेणी
 का अगला पद __________ है |
का अगला पद __________ है | - समांतर श्रेणी में
 तथा
तथा  हो तो
हो तो 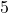 पदों का योग __________ होगा |
पदों का योग __________ होगा | - समांतर श्रेणी में
 तथा
तथा  हो तो सार्व-अंतर
हो तो सार्व-अंतर  एक समांतर श्रेणी है |
एक समांतर श्रेणी है | - यदि
 A.P. में हैं तब
A.P. में हैं तब  है |
है | - श्रेणी
 का 6वां पद
का 6वां पद 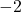 है |
है |  समांतर श्रेणी है |
समांतर श्रेणी है |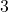 और
और 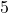 का समांतर माध्य
का समांतर माध्य 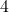 है |
है |- समांतर श्रेणी के
 पदों का योगफल
पदों का योगफल  होता है |
होता है | - यदि
 समांतर श्रेणी है, तो
समांतर श्रेणी है, तो  का मान
का मान  होगा |
होगा |  का सार्व-अंतर
का सार्व-अंतर 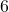 होगा |
होगा | समांतर श्रेणी है |
समांतर श्रेणी है |- समांतर श्रेणी के पदों का योगफल
![Rendered by QuickLaTeX.com S_n = \frac{n}{2}[2a + (n-1)d]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-91f9edcdadf164b00530a88036211226_l3.png) है |
है |
प्र.4 सही जोड़ी बनाइए |
| स्तम्भ – A | स्तम्भ – B |
|---|---|
| (i) व्यापक समांतर श्रेढी (A.P.) | (a) अपरिमित समांतर श्रेढी |
| (ii) ऐसी समांतर श्रेढी जिसमें पदों की संख्या सीमित हो | (b) |
| (iii) ऐसी समांतर श्रेढी जिसमें पदों की संख्या असीमित हो | (c) परिमित समांतर श्रेढी |
| (iv) समांतर श्रेणी का |
(d) |
| (v) समांतर श्रेणी के |
(e) |
प्र.5 एक शब्द / वाक्य में उत्तर दीजिए |
- A.P.:
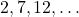 के 10 वें पद का मान लिखिए |
के 10 वें पद का मान लिखिए | - A.P.:
 में पदों की संख्या बताइए |
में पदों की संख्या बताइए |  समांतर श्रेणी है या नहीं?
समांतर श्रेणी है या नहीं? का अगला पद क्या होगा?
का अगला पद क्या होगा? का सार्व-अंतर क्या होगा ?
का सार्व-अंतर क्या होगा ?- यदि किसी श्रेणी के पदों की संख्या सीमित न हो तो उसे क्या कहते हैं ?
 के 8 पदों का योग क्या होगा ?
के 8 पदों का योग क्या होगा ? का 6 वां पद लिखिए |
का 6 वां पद लिखिए |
2 अंक वाले प्रश्न
- समांतर श्रेणी
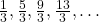 का प्रथम पद एवं सार्व-अंतर ज्ञात कीजिए |
का प्रथम पद एवं सार्व-अंतर ज्ञात कीजिए | - समांतर श्रेणी का प्रथम पद
 और सार्व-अंतर
और सार्व-अंतर  हो तो अगले चार पद लिखिए |
हो तो अगले चार पद लिखिए | - समांतर श्रेणी
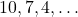 का 10 वां पद ज्ञात कीजिए |
का 10 वां पद ज्ञात कीजिए | - श्रेणी
 का 6वां पद ज्ञात कीजिए |
का 6वां पद ज्ञात कीजिए | - यदि
 हो तो प्रथम दो पद ज्ञात कीजिए |
हो तो प्रथम दो पद ज्ञात कीजिए | - समांतर श्रेणी
 में कितने पद हैं?
में कितने पद हैं? - समांतर श्रेणी का प्रथम पद एवं सार्व-अंतर ज्ञात कीजिए जिसका तीसरा पद 5 और 7 वां पद 9 है |
- किसी समांतर श्रेणी का 17 वां पद उसके 10 वे पद से 7 अधिक है | इसका सार्व-अंतर ज्ञात कीजिए |
3 अंक वाले प्रश्न
- समांतर श्रेणी
 का कौनसा पद
का कौनसा पद  है?
है? - क्या संख्याओं की सूची
 का कोई पद
का कोई पद  है? क्यों?
है? क्यों? - श्रेणी
 का कौनसा पद
का कौनसा पद  होगा?
होगा? - क्या A.P.:
 का एक पद
का एक पद  है? क्यों?
है? क्यों? - वह A.P. ज्ञात कीजिए जिसका तीसरा पद
 है और 7 वां पद 5 वें पद से
है और 7 वां पद 5 वें पद से 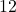 अधिक है |
अधिक है | - समांतर श्रेणी
 का कौनसा पद उसके 54वें पद से
का कौनसा पद उसके 54वें पद से  अधिक होगा?
अधिक होगा? - 5 के प्रथम 10 गुणजों का योग ज्ञात कीजिए |
- ऐसे प्रथम 10 धनात्मक पूर्णांकों का योग ज्ञात कीजिए जो 5 से विभाज्य हों |
- समांतर श्रेणी
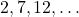 के 10 पदों तक योग ज्ञात कीजिए |
के 10 पदों तक योग ज्ञात कीजिए | - तीन अंकों वाली कितनी संख्याएँ 7 से विभाज्य हैं |
- दो अंकों वाली कितनी संख्याएँ 3 से विभाज्य हैं |
- यदि किसी समांतर श्रेणी के तीसरे और नौवें पद क्रमशः
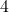 और
और 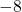 हैं, तो इसका कौनसा पद शून्य होगा?
हैं, तो इसका कौनसा पद शून्य होगा? - 10 और 250 के बीच में 4 के कितने गुणज हैं?
- उस A.P. का 31 वां पद ज्ञात कीजिए, जिसका 11 वां पद 38 है और 16 वां पद 73 है |
- वह A.P. निर्धारित कीजिए, जिसका तीसरा पद 5 और 7 वां पद 9 है |
- समांतर श्रेणी
 के कितने पद लिए जाएँ ताकि उनका योग
के कितने पद लिए जाएँ ताकि उनका योग  हो ?
हो ? - 0 और 50 के बीच की विषम संख्याओं का योग ज्ञात कीजिए |
- फूलों की एक क्यारी की पहली पंक्ति में 23 गुलाब के पौधे हैं, दूसरी पंक्ति में 21 गुलाब के पौधे हैं, तीसरी पंक्ति में 19 गुलाब के पौधे हैं, इत्यादि उसकी अंतिम पंक्ति में 5 गुलाब के पौधे हैं | इस क्यारी में कुल कितनी पंक्तियाँ हैं?
 के किस मान के लिए दोनों समांतर श्रेणियों
के किस मान के लिए दोनों समांतर श्रेणियों  और
और 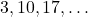 के
के  वें पद बराबर होंगे |
वें पद बराबर होंगे |- प्रथम 100 धन पूर्णांक संख्याओं का योग ज्ञात कीजिए |
- किसी स्कूल के विद्यार्थियों को उनके समग्र शैक्षिक प्रदर्शन के लिए 7 नकद पुरस्कार देने के लिए ₹ 700 की राशि रखी गई है | यदि प्रत्येक पुरस्कार अपने से ठीक पहले पुरस्कार से ₹ 20 कम है, तो प्रत्येक पुरस्कार का मान ज्ञात कीजिए |
- 0 और 50 के बीच की विषम संख्याओं का योग ज्ञात कीजिए |
- यदि किसी A.P. के प्रथम
 पदों का योग
पदों का योग  है, तो इसके दो पदों का योग कितना होगा?
है, तो इसके दो पदों का योग कितना होगा?
अध्याय 6: त्रिभुज
1 अंक वाले प्रश्न
प्र.1. सही विकल्प चुनिये:
- यदि किसी त्रिभुज की एक भुजा के समान्तर अन्य दो भुजाओं को भिन्न-भिन्न बिन्दुओं पर प्रतिच्छेद करने के लिए एक रेखा खींची जाए, तो ये अन्य दो भुजाएँ एक ही अनुपात में विभाजित हो जाती हैं। इस कथन को निम्नलिखित नाम से जाना जाता है:
- किसी
 में
में  तथा
तथा  ,
,  ,
,  तब
तब  होगा:
होगा: - किसी त्रिभुज
 में
में  है |
है |  ,
,  ,
,  तथा
तथा  तब
तब  का मान होगा:
का मान होगा:
(A) आधारभूत आनुपातिकता प्रमेय (B) पाइथागोरस प्रमेय (C) RHS प्रमेय (D) इनमें से कोई नहीं
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
प्र.2 रिक्त स्थान की पूर्ति कीजिए |
- सभी वृत्त __________ होते हैं | (सर्वांगसम, समरूप)
- सभी वर्ग __________ होते हैं | (सर्वांगसम, समरूप)
- सभी __________ त्रिभुज समरूप होते हैं | (समद्विबाहु, समबाहु)
- दो समान कोणिक त्रिभुजों में उनकी संगत भुजाओं का अनुपात सदैव __________ होता है | (समान, असमान)
- यदि एक रेखा किसी त्रिभुज की दो भुजाओं को एक ही अनुपात में विभाजित करे, तो कि वह तीसरी भुजा के __________ होती है | (समांतर, असमांतर)
प्र.3 सत्य / असत्य लिखिए |
- दो त्रिभुजों में संगत कोण बराबर हों, तो उनकी संगत भुजाएँ एक ही अनुपात में (समानुपाती) होती हैं और इसीलिए ये त्रिभुज समरूप होते हैं |
- यदि एक त्रिभुज के दो कोण एक अन्य त्रिभुज के क्रमश: दो कोणों के बराबर हों, तो त्रिभुज समरूप होते हैं |
प्र.4 सही जोड़ी बनाइए |
| स्तम्भ – A | स्तम्भ – B |
|---|---|
| (i) समरूप आकृतियाँ | (a) समरूप होती हैं, परन्तु इसका विलोम सत्य नहीं है | |
| (ii) सर्वांगसम आकृतियाँ | (b) आकृतियाँ जिनके आकार समान हों, परन्तु आमाप आवश्यक रूप से समान न हों | |
| (iii) दो समरूप त्रिभुजों की संगत भुजाएँ | (c) बराबर होते हैं | |
| (iv) दो समरूप त्रिभुजों के संगत कोण | (d) समानुपातिक होती हैं | |
प्र.5 एक शब्द / वाक्य में उत्तर दीजिए |
- क्या सभी समद्विबाहु त्रिभुज समरूप होते हैं |
- क्या सभी वर्ग समरूप होते हैं |
2 अंक वाले प्रश्न
- समरूप आकृतियों को परिभाषित कीजिए |
- बहुभुजों की समरूपता के आवश्यक प्रतिबन्ध लिखिए |
- त्रिभुजों की समरूपता के आवश्यक प्रतिबन्ध लिखिए |
 में यदि
में यदि  तो क्या
तो क्या  है ? समझाइए |
है ? समझाइए |- आकृति में
 है |
है |  ज्ञात कीजिए |
ज्ञात कीजिए |
- आकृति में
 है |
है |  ज्ञात कीजिए |
ज्ञात कीजिए |
- लम्बाई
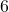 मी. वाले एक ऊर्ध्वाधर स्तंभ की भूमि पर छाया की लम्बाई
मी. वाले एक ऊर्ध्वाधर स्तंभ की भूमि पर छाया की लम्बाई 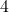 मी. है, जबकि उसी समय एक मीनार की छाया की लम्बाई
मी. है, जबकि उसी समय एक मीनार की छाया की लम्बाई 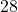 मी. है | मीनार की ऊँचाई ज्ञात कीजिए |
मी. है | मीनार की ऊँचाई ज्ञात कीजिए | - आकृति में,
 ,
,  और
और  है |
है |  ,
,  और
और  ज्ञात कीजिए |
ज्ञात कीजिए |
- किसी त्रिभुज
 की भुजाओं
की भुजाओं  और
और  पर क्रमशः बिंदु
पर क्रमशः बिंदु 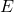 और
और 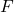 स्थित हैं | बताइए क्या
स्थित हैं | बताइए क्या  है, यदि
है, यदि  ,
,  ,
,  और
और  |
| - किसी त्रिभुज
 की भुजाओं
की भुजाओं  और
और  पर क्रमशः बिंदु
पर क्रमशः बिंदु 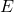 और
और 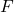 स्थित हैं | बताइए क्या
स्थित हैं | बताइए क्या  है, यदि
है, यदि  ,
,  ,
,  और
और  |
| - किसी त्रिभुज
 की भुजाओं
की भुजाओं  और
और  पर क्रमशः बिंदु
पर क्रमशः बिंदु 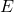 और
और 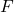 स्थित हैं | बताइए क्या
स्थित हैं | बताइए क्या  है, यदि
है, यदि  ,
,  ,
,  और
और  |
| - समरूप आकृतियों के दो भिन्न-भिन्न उदाहरण दीजिए |
- आकृति में
 है | दर्शाइए कि
है | दर्शाइए कि  और
और  |
|
4 अंक वाले प्रश्न
 की लम्बाई वाली एक लड़की बल्ब लगे एक खम्भे के आधार से परे
की लम्बाई वाली एक लड़की बल्ब लगे एक खम्भे के आधार से परे  की चाल से चल रही है | यदि बल्ब भूमि से
की चाल से चल रही है | यदि बल्ब भूमि से  की ऊँचाई पर है, तो
की ऊँचाई पर है, तो 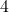 सेकंड बाद उस लड़की की छाया की लम्बाई ज्ञात कीजिए |
सेकंड बाद उस लड़की की छाया की लम्बाई ज्ञात कीजिए |- यदि कोई रेखा एक
 की भुजाओं
की भुजाओं 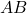 और
और  को क्रमशः
को क्रमशः 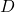 और
और 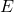 पर प्रतिच्छेद करे तथा भुजा
पर प्रतिच्छेद करे तथा भुजा  के समांतर हो, तो सिद्ध कीजिए कि
के समांतर हो, तो सिद्ध कीजिए कि  होगा |
होगा | - आकृति में
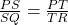 तथा
तथा  है | सिद्ध कीजिए कि
है | सिद्ध कीजिए कि  एक समद्विबाहु त्रिभुज है |
एक समद्विबाहु त्रिभुज है |
- ABCD एक समलम्ब है जिसमें
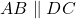 है तथा इसके विकर्ण परस्पर बिंदु
है तथा इसके विकर्ण परस्पर बिंदु  पर प्रतिच्छेद करते हैं | दर्शाइए कि
पर प्रतिच्छेद करते हैं | दर्शाइए कि  है |
है | - यदि किसी त्रिभुज की एक भुजा के समान्तर अन्य दो भुजाओं की भिन्न-भिन्न बिन्दुओं पर प्रतिच्छेद करने के लिए एक रेखा खींची जाए, तो ये अन्य भुजाएँ एक ही अनुपात में विभाजित हो जाती हैं | सिद्ध कीजिए |
- यदि एक रेखा किसी त्रिभुज की दो भुजाओं को एक ही अनुपात में विभाजित करे, तो वह तीसरी भुजा के समांतर होती है | सिद्ध कीजिए |