MP Board 10th Mathematics Chapter 1.2 Repetition of Irrational Number :
सिद्ध करें कि  एक अपरिमेय संख्या है
एक अपरिमेय संख्या है
मान लीजिए कि ![]() एक परिमेय संख्या है। इसका अर्थ है कि
एक परिमेय संख्या है। इसका अर्थ है कि ![]() को दो पूर्णांकों
को दो पूर्णांकों ![]() और
और ![]() के अनुपात के रूप में व्यक्त किया जा सकता है, जहाँ
के अनुपात के रूप में व्यक्त किया जा सकता है, जहाँ ![]() और
और ![]() और
और ![]() का कोई उभयनिष्ठ गुणनखंड नहीं है (अर्थात, भिन्न अपरिमेय रूप में है)।
का कोई उभयनिष्ठ गुणनखंड नहीं है (अर्थात, भिन्न अपरिमेय रूप में है)।
इसलिए, हम लिख सकते हैं:
![]()
दोनों पक्षों को वर्ग करने पर:
![]()
![]()
![]()
यह समीकरण दर्शाता है कि ![]() एक सम संख्या है (क्योंकि यह 2 का गुणज है)। यदि
एक सम संख्या है (क्योंकि यह 2 का गुणज है)। यदि ![]() सम है, तो
सम है, तो ![]() भी सम होना चाहिए, क्योंकि किसी विषम संख्या का वर्ग विषम होता है।
भी सम होना चाहिए, क्योंकि किसी विषम संख्या का वर्ग विषम होता है।
मान लें ![]() , जहाँ
, जहाँ ![]() एक पूर्णांक है। इसे
एक पूर्णांक है। इसे ![]() में प्रतिस्थापित करें:
में प्रतिस्थापित करें:
![]()
![]()
![]()
यह दर्शाता है कि ![]() भी सम है, और इसलिए
भी सम है, और इसलिए ![]() भी सम होना चाहिए।
भी सम होना चाहिए।
अब, यदि ![]() और
और ![]() दोनों सम हैं, तो उनके पास कम से कम 2 का एक उभयनिष्ठ गुणनखंड है। यह हमारी प्रारंभिक धारणा के विपरीत है कि
दोनों सम हैं, तो उनके पास कम से कम 2 का एक उभयनिष्ठ गुणनखंड है। यह हमारी प्रारंभिक धारणा के विपरीत है कि ![]() और
और ![]() का कोई उभयनिष्ठ गुणनखंड नहीं है।
का कोई उभयनिष्ठ गुणनखंड नहीं है।
इसलिए, हमारी धारणा कि ![]() एक परिमेय संख्या है, गलत है। अतः,
एक परिमेय संख्या है, गलत है। अतः, ![]() एक अपरिमेय संख्या है।
एक अपरिमेय संख्या है।
सिद्ध करें कि  एक अपरिमेय संख्या है
एक अपरिमेय संख्या है
मान लीजिए कि ![]() एक परिमेय संख्या है। इसका अर्थ है कि
एक परिमेय संख्या है। इसका अर्थ है कि ![]() को दो पूर्णांकों
को दो पूर्णांकों ![]() और
और ![]() के अनुपात के रूप में व्यक्त किया जा सकता है, जहाँ
के अनुपात के रूप में व्यक्त किया जा सकता है, जहाँ ![]() और
और ![]() और
और ![]() का कोई उभयनिष्ठ गुणनखंड नहीं है (अर्थात, भिन्न अपरिमेय रूप में है)।
का कोई उभयनिष्ठ गुणनखंड नहीं है (अर्थात, भिन्न अपरिमेय रूप में है)।
इसलिए, हम लिख सकते हैं:
![]()
दोनों पक्षों को वर्ग करने पर:
![]()
![]()
![]()
यह समीकरण दर्शाता है कि ![]() 3 का गुणज है। इसलिए,
3 का गुणज है। इसलिए, ![]() भी 3 का गुणज होना चाहिए (क्योंकि यदि
भी 3 का गुणज होना चाहिए (क्योंकि यदि ![]() 3 से विभाज्य नहीं है, तो
3 से विभाज्य नहीं है, तो ![]() भी 3 से विभाज्य नहीं होगा, जो कि समीकरण के विपरीत है)।
भी 3 से विभाज्य नहीं होगा, जो कि समीकरण के विपरीत है)।
मान लें ![]() , जहाँ
, जहाँ ![]() एक पूर्णांक है। इसे
एक पूर्णांक है। इसे ![]() में प्रतिस्थापित करें:
में प्रतिस्थापित करें:
![]()
![]()
![]()
यह दर्शाता है कि ![]() भी 3 का गुणज है, और इसलिए
भी 3 का गुणज है, और इसलिए ![]() भी 3 का गुणज होना चाहिए।
भी 3 का गुणज होना चाहिए।
अब, यदि ![]() और
और ![]() दोनों 3 से विभाज्य हैं, तो उनके पास कम से कम 3 का एक उभयनिष्ठ गुणनखंड है। यह हमारी प्रारंभिक धारणा के विपरीत है कि
दोनों 3 से विभाज्य हैं, तो उनके पास कम से कम 3 का एक उभयनिष्ठ गुणनखंड है। यह हमारी प्रारंभिक धारणा के विपरीत है कि ![]() और
और ![]() का कोई उभयनिष्ठ गुणनखंड नहीं है।
का कोई उभयनिष्ठ गुणनखंड नहीं है।
इसलिए, हमारी धारणा कि ![]() एक परिमेय संख्या है, गलत है। अतः,
एक परिमेय संख्या है, गलत है। अतः, ![]() एक अपरिमेय संख्या है।
एक अपरिमेय संख्या है।
यह साबित करें कि 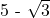 एक अपरिमेय संख्या है
एक अपरिमेय संख्या है
सिद्ध करने की प्रक्रिया:
मान लेते हैं कि ![]() एक परिमेय संख्या है। अर्थात् इसे
एक परिमेय संख्या है। अर्थात् इसे ![]() के रूप में लिखा जा सकता है, जहां
के रूप में लिखा जा सकता है, जहां ![]() परिमेय संख्याएँ हैं और
परिमेय संख्याएँ हैं और ![]() ।
।
पुनर्व्यवस्थित करें:
![]()
![]()
चूंकि ![]() और
और ![]() परिमेय संख्याएँ हैं, तो
परिमेय संख्याएँ हैं, तो ![]() भी परिमेय संख्या होगी।
भी परिमेय संख्या होगी।
लेकिन ![]() ज्ञात रूप से अपरिमेय संख्या है, जिससे विरोधाभास उत्पन्न होता है।
ज्ञात रूप से अपरिमेय संख्या है, जिससे विरोधाभास उत्पन्न होता है।
अतः हमारा प्रारंभिक अनुमान गलत था। इसलिए, ![]() एक अपरिमेय संख्या है।
एक अपरिमेय संख्या है।
प्रश्नावली 1.3
प्रश्न 1: 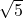
हम इसे विरोधाभास की विधि (contradiction method) से सिद्ध करेंगे।
- मान लीजिए कि
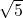 एक परिमेय संख्या है, अर्थात इसे
एक परिमेय संख्या है, अर्थात इसे  के रूप में लिखा जा सकता है, जहाँ
के रूप में लिखा जा सकता है, जहाँ 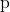 और
और  सहप्राइम हैं (अर्थात उनका महत्तम समापवर्तक 1 है) और
सहप्राइम हैं (अर्थात उनका महत्तम समापवर्तक 1 है) और 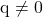 ।
। ![Rendered by QuickLaTeX.com \[\sqrt{5} = \frac{p}{q}\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-b4b881497b52ab9d56baad4ca623e3ff_l3.png)
- दोनों ओर स्क्वायर करते हैं:
![Rendered by QuickLaTeX.com \[5 = \frac{p^2}{q^2}\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-bf8d34e044f016b652a67cd5cfdbdc23_l3.png)
- इससे मिलता है:
![Rendered by QuickLaTeX.com \[p^2 = 5q^2\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-7371a414b47244a83275a55163e5be4a_l3.png)
- इसका अर्थ है कि
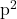 5 से विभाजित है, जिससे
5 से विभाजित है, जिससे 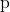 भी 5 से विभाजित होगा। अतः हम
भी 5 से विभाजित होगा। अतः हम 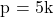 लिख सकते हैं।
लिख सकते हैं। - इसे उपरोक्त समीकरण में रखते हैं:
![Rendered by QuickLaTeX.com \[(5k)^2 = 5q^2\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-ef0ec7e9bc2aae8accf6bbb886bb60d0_l3.png)
![Rendered by QuickLaTeX.com \[25k^2 = 5q^2\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-c391be2a203ee1c55562a8984e72a526_l3.png)
![Rendered by QuickLaTeX.com \[q^2 = 5k^2\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-2c084a8047d09b4848799ee90908e5a2_l3.png)
- इससे पता चलता है कि
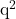 भी 5 से विभाजित है, अर्थात
भी 5 से विभाजित है, अर्थात  भी 5 से विभाजित होगा।
भी 5 से विभाजित होगा। - लेकिन
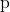 और
और  सहप्राइम थे, इसलिए दोनों 5 से विभाजित नहीं हो सकते। यह हमारी प्रारंभिक धारणा का खंडन करता है।
सहप्राइम थे, इसलिए दोनों 5 से विभाजित नहीं हो सकते। यह हमारी प्रारंभिक धारणा का खंडन करता है।
इसलिए, हमारा मानना कि ![]() परिमेय है, गलत सिद्ध हुआ। अतः
परिमेय है, गलत सिद्ध हुआ। अतः ![]() अपरिमेय संख्या है।
अपरिमेय संख्या है।
प्रश्न 2: 
- मान लीजिए कि
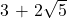 परिमेय संख्या है, यानी इसे
परिमेय संख्या है, यानी इसे 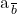 के रूप में लिखा जा सकता है।
के रूप में लिखा जा सकता है। ![Rendered by QuickLaTeX.com \[3 + 2\sqrt{5} = \frac{a}{b}\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-62eb67ae6e766b460f7d4ba359d69aad_l3.png)
- इससे हमें मिलता है:
![Rendered by QuickLaTeX.com \[2\sqrt{5} = \frac{a}{b} - 3\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-b06930f2b5b1246ec0edce60e1a9168a_l3.png)
![Rendered by QuickLaTeX.com \[\sqrt{5} = \frac{a - 3b}{2b}\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-edd931f6aa3b0de705d14d739d7825ea_l3.png)
- दाएँ पक्ष परिमेय संख्या है, लेकिन बाएँ पक्ष अपरिमेय (
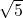 ) है, जिससे विरोधाभास उत्पन्न होता है।
) है, जिससे विरोधाभास उत्पन्न होता है। - इसलिए,
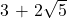 अपरिमेय संख्या है।
अपरिमेय संख्या है।
प्रश्न 3: 
- (i)
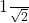
–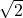 पहले ही अपरिमेय सिद्ध किया जा चुका है।
पहले ही अपरिमेय सिद्ध किया जा चुका है।
– यदि कोई संख्या अपरिमेय है, तो उसका व्युत्क्रम भी अपरिमेय होगा।
– अतः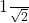 अपरिमेय है।
अपरिमेय है। - (ii)

–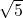 अपरिमेय संख्या है।
अपरिमेय संख्या है।
– जब किसी अपरिमेय संख्या को गैर-शून्य परिमेय संख्या (जैसे 7) से गुणा किया जाता है, तो परिणाम भी अपरिमेय होता है।
– अतः अपरिमेय है।
अपरिमेय है। - (iii)
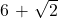
–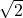 अपरिमेय संख्या है।
अपरिमेय संख्या है।
– किसी अपरिमेय संख्या में किसी परिमेय संख्या को जोड़ने पर परिणाम अपरिमेय ही होता है।
– अतः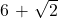 अपरिमेय है।
अपरिमेय है।
प्रश्नावली 1.4
प्रश्न 1: बिना लंबी विभाजन प्रक्रिया किए बताइए कि निम्नलिखित परिमेय संख्याओं के दशमलव प्रसार सांत हैं या असांत आवर्ती हैं।
हल:कोई भी परिमेय संख्या  का दशमलव प्रसार सांत होगा यदि
का दशमलव प्रसार सांत होगा यदि  के अभाज्य गुणनखंड केवल 2 और 5 हों। यदि
के अभाज्य गुणनखंड केवल 2 और 5 हों। यदि  में कोई अन्य अभाज्य संख्या (जैसे 3, 7, 11, 23 आदि) हो, तो उसका दशमलव प्रसार असांत आवर्ती होगा।
में कोई अन्य अभाज्य संख्या (जैसे 3, 7, 11, 23 आदि) हो, तो उसका दशमलव प्रसार असांत आवर्ती होगा।
अब प्रत्येक संख्या की जाँच करते हैं:
| संख्या | भाजक | दशमलव प्रसार |
|---|---|---|
| सांत | ||
| सांत | ||
| असांत आवर्ती | ||
| सांत | ||
| असांत आवर्ती | ||
| असांत आवर्ती | ||
| असांत आवर्ती | ||
| सांत | ||
| असांत आवर्ती |
निष्कर्ष:
सांत दशमलव प्रसार वाली संख्याएँ: ![]() ,
, ![]() ,
, ![]() ,
, ![]()
असांत आवर्ती दशमलव प्रसार वाली संख्याएँ: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()