दो चर वाले रैखिक समीकरण युग्म :MP Board 10th Linear Equation with Two Variables Question Bank
स्मरणीय बिंदु :
- वह समीकरण जिसको
 के रूप में रखा जा सकता है और
के रूप में रखा जा सकता है और 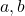 और
और  वास्तविक संख्याऐं हैं और
वास्तविक संख्याऐं हैं और  और
और  दोनों शून्य नहीं हैं, दो चरों
दोनों शून्य नहीं हैं, दो चरों  और
और  में एक रैखिक समीकरण कहलाता है |
में एक रैखिक समीकरण कहलाता है | - दो चर वाले किसी रैखिक समीकरण का प्रत्येक हल उसको निरूपित करने वाली रेखा पर स्थित एक बिंदु होता है |
- दो चरों वाले रैखिक समीकरण
 का प्रत्येक हल
का प्रत्येक हल 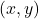 इस समीकरण को निरूपित करने वाली रेखा के एक बिंदु के संगत होता है और विलोमतः भी ऐसा होता है |
इस समीकरण को निरूपित करने वाली रेखा के एक बिंदु के संगत होता है और विलोमतः भी ऐसा होता है |
प्र.1 सही विकल्प चुनिए|
1. निम्नलिखित में से दो चरों में रैखिक समीकरण है :
(A) ![]()
(B) ![]()
(C) ![]()
(D) ![]()
उत्तर: (D) ![]()
(स्पष्टीकरण: एक रैखिक समीकरण में चरों (x, y) की घात 1 होती है।)
2. यदि ![]() तो रैखिक समीकरण युग्म
तो रैखिक समीकरण युग्म ![]() तथा
तथा ![]() का
का
(A) एक अद्वितीय हल होगा |
(B) कोई हल नहीं होगा |
(C) अनन्तः अनेक हल होंगे |
(D) इनमें से कोई नहीं |
उत्तर: (A) एक अद्वितीय हल होगा |
3. यदि ![]() तो रैखिक समीकरण युग्म
तो रैखिक समीकरण युग्म ![]() तथा
तथा ![]() का
का
(A) एक अद्वितीय हल होगा |
(B) कोई हल नहीं होगा |
(C) अनन्तः अनेक हल होंगे |
(D) इनमें से कोई नहीं |
उत्तर: (B) कोई हल नहीं होगा |
4. यदि ![]() तो रैखिक समीकरण युग्म
तो रैखिक समीकरण युग्म ![]() तथा
तथा ![]() का
का
(A) एक अद्वितीय हल होगा |
(B) कोई हल नहीं होगा |
(C) अनन्तः अनेक हल होंगे |
(D) इनमें से कोई नहीं |
उत्तर: (C) अनन्तः अनेक हल होंगे |
5. रैखिक समीकरण युग्म ![]() तथा
तथा ![]() का एक अद्वितीय हल होने की शर्त है:
का एक अद्वितीय हल होने की शर्त है:
(A) ![]()
(B) ![]()
(C) ![]()
(D) इनमें से कोई नहीं |
उत्तर: (A) ![]()
6. रैखिक समीकरण युग्म ![]() तथा
तथा ![]() का कोई हल नहीं होने की शर्त है:
का कोई हल नहीं होने की शर्त है:
(A) ![]()
(B) ![]()
(C) ![]()
(D) इनमें से कोई नहीं |
उत्तर: (B) ![]()
7. रैखिक समीकरण युग्म ![]() तथा
तथा ![]() के अनंत अनेक हल होने की शर्त है:
के अनंत अनेक हल होने की शर्त है:
(A) ![]()
(B) ![]()
(C) ![]()
(D) इनमें से कोई नहीं |
उत्तर: (C) ![]()
प्र.2 रिक्त स्थान की पूर्ति कीजिए।
- समीकरण
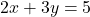 में यदि
में यदि 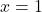 तो
तो 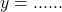 होगा |
होगा |
- हल:
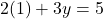
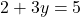
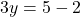
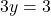
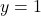
- उत्तर: 1
- हल:
- वह समीकरण जिसको
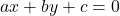 के रूप में रखा जा सकता है, जहाँ
के रूप में रखा जा सकता है, जहाँ  और
और  वास्तविक संख्याएँ हैं और
वास्तविक संख्याएँ हैं और  और
और  दोनों शून्य नहीं हैं, दो चरों
दोनों शून्य नहीं हैं, दो चरों  और
और  में एक \text{……} समीकरण कहलाता है |
में एक \text{……} समीकरण कहलाता है |
- उत्तर: रैखिक
- समीकरण
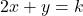 में यदि
में यदि 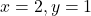 हो तो
हो तो  का मान \text{……} होगा |
का मान \text{……} होगा |
- हल:
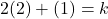
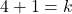
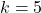
- उत्तर: 5
- हल:
प्र.3 सत्य / असत्य लिखिये |
- दो चरों में एक रैखिक समीकरण के अनेक हल होते हैं |
- उत्तर: सत्य (क्योंकि यह एक सीधी रेखा को निरूपित करता है, जिस पर अनंत बिंदु होते हैं।)
- रैखिक समीकरण का प्रत्येक हल उसको निरूपित करने वाली रेखा पर स्थित एक बिंदु होता है |
- उत्तर: सत्य
- समीकरण निकाय
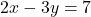 एवं
एवं 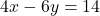 द्वारा निरूपित रेखाएँ प्रतिच्छेदी होंगी |
द्वारा निरूपित रेखाएँ प्रतिच्छेदी होंगी |
- उत्तर: असत्य
- (स्पष्टीकरण: यहाँ
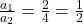 ,
, 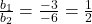 , और
, और 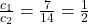 | चूँकि
| चूँकि  है, इसलिए रेखाएँ संपाती (coincident) होंगी, प्रतिच्छेदी नहीं।)
है, इसलिए रेखाएँ संपाती (coincident) होंगी, प्रतिच्छेदी नहीं।)
प्र.4. सही जोड़ी मिलाइए:
| स्तम्भ – अ | स्तम्भ – ब (सही उत्तर) |
| 1. | (ii). |
| 2. दो चरों में रैखिक समीकरण का व्यापक रूप | (i). |
| 3. | (iii). |
| 4. | (v). निकाय द्वारा निरूपित रेखाएँ संपाती |
| 5. | (iv). |
प्र.5 एक शब्द / वाक्य में उत्तर दीजिये।
- दो चरों में रैखिक समीकरण का मानक रूप लिखिए।
उत्तर: , जहाँ
, जहाँ  वास्तविक संख्याएँ हैं, और
वास्तविक संख्याएँ हैं, और  और
और  दोनों शून्य नहीं हैं।
दोनों शून्य नहीं हैं। - रैखिक समीकरण
 में यदि
में यदि  हो तो
हो तो  का क्या मान होगा?
का क्या मान होगा?
हल: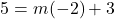
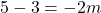
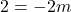
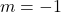
उत्तर: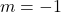
- यदि दो संतरों और पांच सेबों का मूल्य Rs. 70 है, तो इस स्थिति को रैखिक समीकरण के रूप में प्रदर्शित कीजिए।
उत्तर: माना संतरे का मूल्य और सेब का मूल्य
और सेब का मूल्य  है।
है।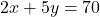
प्र.6 से प्र.30 तक के हल:
प्र.6. तीन बल्लों तथा छः गेंदों की कीमत 3900/-…
हल: माना एक बल्ले की कीमत ![]() रु है और एक गेंद की कीमत
रु है और एक गेंद की कीमत ![]() रु है।
रु है।
(i) ![]()
(ii) ![]()
प्र.7. दो किलो सेब और एक किलो अंगूर का मूल्य 160/-…
हल: माना 1 किलो सेब का मूल्य ![]() रु है और 1 किलो अंगूर का मूल्य
रु है और 1 किलो अंगूर का मूल्य ![]() रु है।
रु है।
(i) ![]()
(ii) ![]()
प्र.8. ![]() तथा
तथा ![]() द्वारा निरूपित रेखाएँ प्रतिच्छेदी, समान्तर या सम्पाती हैं।
द्वारा निरूपित रेखाएँ प्रतिच्छेदी, समान्तर या सम्पाती हैं।
हल:![]()
![]()
चूँकि ![]() है, इसलिए रेखाएँ प्रतिच्छेदी हैं।
है, इसलिए रेखाएँ प्रतिच्छेदी हैं।
प्र.9. ![]() तथा
तथा ![]() समीकरणों के युग्म संगत है या असंगत।
समीकरणों के युग्म संगत है या असंगत।
हल:![]()
![]()
![]() (समीकरणों को
(समीकरणों को ![]() और
और ![]() लिखने पर)
लिखने पर)
चूँकि ![]() है, इसलिए निकाय असंगत है (इसका कोई हल नहीं है)।
है, इसलिए निकाय असंगत है (इसका कोई हल नहीं है)।
प्र.10. दो चरों वाले रैखिक समीकरण युग्म का एक उदाहरण लिखिए, जिसके द्वारा निरूपित रेखाएँ समान्तर हों।
उत्तर: (हमें ![]() की शर्त पूरी करनी है)
की शर्त पूरी करनी है)![]()
![]() (यह संपाती होगा,
(यह संपाती होगा, ![]() )
)
सही उदाहरण:![]()
![]()
(यहाँ ![]() ,
, ![]() ,
, ![]() . अतः
. अतः ![]() )
)
प्र.11. प्रतिस्थापन विधि से हल करें – ![]() (1) और
(1) और ![]() (2)
(2)
हल:
समी. (1) से: ![]()
इसे समी. (2) में रखने पर:![]()
(पूरी समी. को 6 से गुणा करने पर)![]()
![]()
![]()
अब ![]()
उत्तर: ![]()
प्र.12. प्रतिस्थापन विधि से हल करें – ![]() (1) और
(1) और ![]() (2)
(2)
हल:
समी. (1) से: ![]()
इसे समी. (2) में रखने पर:![]()
![]()
![]()
चूँकि ![]() , इसलिए
, इसलिए ![]()
![]()
उत्तर: ![]()
प्र.13. विलोपन विधि से हल कीजिये – ![]() (1) और
(1) और ![]() (2)
(2)
हल:
समी. (1) को 2 से गुणा करने पर: ![]() (3)
(3)
समी. (2) और (3) को जोड़ने पर:![]()
![]()
![]() का मान समी. (1) में रखने पर:
का मान समी. (1) में रखने पर:![]()
उत्तर: ![]()
प्र.14. विलोपन विधि से हल कीजिये – ![]() (1) और
(1) और ![]() (2)
(2)
हल:
समी. (1) को 6 से गुणा करने पर: ![]() (3)
(3)
समी. (2) को 3 से गुणा करने पर: ![]() (4)
(4)
समी. (3) में से (4) को घटाने पर:![]()
![]()
![]() का मान समी. (4) में रखने पर:
का मान समी. (4) में रखने पर:![]()
उत्तर: ![]()
प्र.15. विलोपन विधि से हल करें – ![]() (1) और
(1) और ![]() (2)
(2)
हल:
समीकरणों को व्यवस्थित करने पर:![]() (1)
(1)![]() (2)
(2)
समी. (2) में से (1) को घटाने पर:![]()
![]()
![]() का मान समी. (1) में रखने पर:
का मान समी. (1) में रखने पर:![]()
उत्तर: ![]()
प्र.16. हल करें – ![]() (1) और
(1) और ![]() (2)
(2)
हल:![]() (1)
(1)![]() (2)
(2)
समी. (1) को 3 से गुणा करने पर: ![]() (3)
(3)
समी. (2) में से (3) को घटाने पर:![]()
![]()
![]() का मान समी. (1) में रखने पर:
का मान समी. (1) में रखने पर:![]()
![]()
![]()
उत्तर: ![]()
प्र.17. ![]() (1) और
(1) और ![]() (2) को प्रतिस्थापन विधि से हल कीजिए।
(2) को प्रतिस्थापन विधि से हल कीजिए।
हल:
समी. (1) से: ![]()
इसे समी. (2) में रखने पर:![]()
![]()
![]()
![]()
उत्तर: ![]()
प्र.18. ![]() (1) और
(1) और ![]() (2) को प्रतिस्थापन विधि से हल कीजिए।
(2) को प्रतिस्थापन विधि से हल कीजिए।
हल:
समी. (1) से: ![]()
इसे समी. (2) में रखने पर:![]()
![]()
![]()
उत्तर: ![]()
प्र.19. ![]() (1) और
(1) और ![]() (2) को विलोपन विधि से हल कीजिए।
(2) को विलोपन विधि से हल कीजिए।
हल:
समी. (2) को 7 से गुणा करने पर: ![]() (3)
(3)
समी. (3) में से (1) को घटाने पर:![]()
![]()
![]() का मान समी. (2) में रखने पर:
का मान समी. (2) में रखने पर:![]()
उत्तर: ![]()
प्र.20. ![]() (1) और
(1) और ![]() (2) को विलोपन विधि से हल कीजिए।
(2) को विलोपन विधि से हल कीजिए।
हल:![]() (1)
(1)![]() (2)
(2)
समी. (1) को 3 से गुणा करने पर: ![]() (3)
(3)
समी. (3) में से (2) को घटाने पर:![]()
![]()
![]() का मान समी. (2) में रखने पर:
का मान समी. (2) में रखने पर:![]()
उत्तर: ![]()
प्र.21. ![]() (1) और
(1) और ![]() (2) को प्रतिस्थापन विधि से हल कीजिए।
(2) को प्रतिस्थापन विधि से हल कीजिए।
हल:
समी. (2) से: ![]()
इसे समी. (1) में रखने पर:![]()
![]()
![]()
उत्तर: ![]()
प्र.22. ![]() (1) और
(1) और ![]() (2) को प्रतिस्थापन विधि से हल कीजिए।
(2) को प्रतिस्थापन विधि से हल कीजिए।
हल:
समी. (2) से: ![]()
इसे समी. (1) में रखने पर:![]()
![]()
![]()
उत्तर: ![]()
प्र.23. दो व्यक्तियों की आय का अनुपात 9:7 है… यदि प्रत्येक 2000 बचा लेता है…
हल:
माना आय ![]() और
और ![]() है।
है।
माना व्यय (खर्च) ![]() और
और ![]() है।
है।
बचत = आय – व्यय![]() (1)
(1)![]() (2)
(2)
समी. (1) को 3 से और समी. (2) को 4 से गुणा करने पर:![]() (3)
(3)![]() (4)
(4)
समी. (4) में से (3) को घटाने पर:![]()
![]()
![]() का मान समी. (1) में रखने पर:
का मान समी. (1) में रखने पर:![]()
![]()
मासिक आय:
व्यक्ति 1: ![]() रु
रु
व्यक्ति 2: ![]() रु
रु
उत्तर: उनकी मासिक आय Rs. 18000 और Rs. 14000 हैं।
प्र.24. ‘k’ के किस मान के लिए… अपरिमित रूप से अनेक हल होंगे?![]()
![]()
हल:
शर्त: ![]()
![]()
(i) ![]() या
या ![]()
(ii) ![]() . यदि
. यदि ![]() , तो
, तो ![]()
दोनों शर्तों को ![]() संतुष्ट करता है।
संतुष्ट करता है।
(![]() जाँच:
जाँच: ![]() ,
, ![]() ,
, ![]() . यहाँ
. यहाँ ![]() , इसलिए
, इसलिए ![]() नहीं है।)
नहीं है।)
उत्तर: ![]()
प्र.25. ![]() (1) और
(1) और ![]() (2) को हल कीजिए और
(2) को हल कीजिए और ![]() का मान ज्ञात कीजिए…
का मान ज्ञात कीजिए… ![]()
हल:
समी. (1) में से (2) को घटाने पर:![]()
![]()
![]() का मान समी. (1) में रखने पर:
का मान समी. (1) में रखने पर:![]()
अब ![]() को
को ![]() में रखने पर:
में रखने पर:![]()
![]()
उत्तर: ![]()
प्र.26. दो संपूरक कोणों में बड़ा कोण छोटे कोण से 18 डिग्री अधिक है।
हल:
माना कोण ![]() और
और ![]() हैं (
हैं (![]() )।
)।
संपूरक (Supplementary): ![]() (1)
(1)![]() (2)
(2)
समी. (2) को (1) में रखने पर:![]()
![]()
![]()
उत्तर: कोण 99° और 81° हैं।
प्र.27. 7 बल्ले तथा 6 गेंदें ₹3800 में… 3 बल्ले तथा 5 गेंदें ₹1750 में…
हल:
माना बल्ले का मूल्य ![]() रु और गेंद का मूल्य
रु और गेंद का मूल्य ![]() रु है।
रु है।![]() (1)
(1)![]() (2)
(2)
समी. (1) को 3 से और समी. (2) को 7 से गुणा करने पर:![]() (3)
(3)![]() (4)
(4)
समी. (4) में से (3) को घटाने पर:![]()
![]() का मान समी. (2) में रखने पर:
का मान समी. (2) में रखने पर:![]()
उत्तर: बल्ले का मूल्य = ₹500, गेंद का मूल्य = ₹50
प्र.28. दो अंकों की एक संख्या एवं उसके अंकों को उलटने पर बनी संख्या का योग 66 है। यदि संख्या के अंकों का अंतर 6 हो…
हल:
माना संख्या ![]() है (x दहाई, y इकाई)।
है (x दहाई, y इकाई)।
उलटी संख्या: ![]()
(i) ![]() (1)
(1)
(ii) ![]() (2) या
(2) या ![]() (3)
(3)
Case 1: समी. (1) और (2) को जोड़ने पर:![]()
![]() . संख्या = 60
. संख्या = 60
Case 2: समी. (1) और (3) को जोड़ने पर:![]()
![]() . संख्या = 06 (यह दो अंकों की संख्या नहीं है)
. संख्या = 06 (यह दो अंकों की संख्या नहीं है)
उत्तर: संख्या 60 है। (ऐसी केवल एक संख्या है)।
प्र.29. ![]() के किन मानों के लिए… अद्वितीय हल है:
के किन मानों के लिए… अद्वितीय हल है: ![]() और
और ![]()
हल:
शर्त: ![]()
![]()
![]()
उत्तर: ![]() के 4 के अतिरिक्त अन्य सभी वास्तविक मानों के लिए।
के 4 के अतिरिक्त अन्य सभी वास्तविक मानों के लिए।
प्र.30. ![]() के किन मानों के लिए… कोई हल नहीं है:
के किन मानों के लिए… कोई हल नहीं है: ![]() और
और ![]()
हल:
शर्त: ![]()
![]()
(i) ![]()
![]()
![]()
(ii) जाँच: ![]()
![]() रखने पर:
रखने पर: ![]() (शर्त सत्य है)
(शर्त सत्य है)
उत्तर: ![]()
प्र.31. 5 पेंसिल तथा 7 कलमों का कुल मूल्य Rs. 50 है…
हल:
माना 1 पेंसिल का मूल्य ![]() रु है।
रु है।
माना 1 कलम का मूल्य ![]() रु है।
रु है।
(i) ![]()
(ii) ![]()
समी. (i) को 7 से और समी. (ii) को 5 से गुणा करने पर:
(iii) ![]()
(iv) ![]()
समी. (iii) में से (iv) को घटाने पर:![]()
![]() का मान समी. (i) में रखने पर:
का मान समी. (i) में रखने पर:![]()
उत्तर: 1 पेंसिल का मूल्य = ₹3, 1 कलम का मूल्य = ₹5.
प्र.32. 5 संतरों और 3 सेबों का मूल्य Rs. 35 है…
हल:
माना 1 संतरे का मूल्य ![]() रु है।
रु है।
माना 1 सेब का मूल्य ![]() रु है।
रु है।
(i) ![]()
(ii) ![]()
![]() का मान समी. (i) में रखने पर (प्रतिस्थापन विधि):
का मान समी. (i) में रखने पर (प्रतिस्थापन विधि):![]()
![]()
![]()
![]()
उत्तर: 1 संतरे का मूल्य = ₹4, 1 सेब का मूल्य = ₹5.
प्र.33. पांच वर्ष पूर्व नूरी की आयु सोनू की आयु की तीन गुनी थी…
हल:
माना नूरी की वर्तमान आयु ![]() वर्ष है।
वर्ष है।
माना सोनू की वर्तमान आयु ![]() वर्ष है।
वर्ष है।
(i) पांच वर्ष पूर्व:![]()
(ii) दस वर्ष पश्चात:![]()
समी. (ii) में से (i) को घटाने पर:![]()
![]()
![]() का मान समी. (ii) में रखने पर:
का मान समी. (ii) में रखने पर:![]()
उत्तर: नूरी की वर्तमान आयु = 50 वर्ष, सोनू की वर्तमान आयु = 20 वर्ष।
प्र.34. दो संख्याओं का अंतर 26 है और एक संख्या दूसरी संख्या की तीन गुनी है।
हल:
माना संख्याएँ ![]() और
और ![]() हैं (
हैं (![]() )।
)।
(i) ![]()
(ii) ![]()
![]() का मान समी. (i) में रखने पर:
का मान समी. (i) में रखने पर:![]()
![]()
उत्तर: संख्याएँ 39 और 13 हैं।
प्र.35. एक भिन्न ![]() हो जाती है, जब उसके अंश से एक घटाया जाये…
हो जाती है, जब उसके अंश से एक घटाया जाये…
हल:
माना भिन्न ![]() है।
है।
(i) ![]()
(ii) ![]()
समी. (i) से ![]() का मान समी. (ii) में रखने पर:
का मान समी. (ii) में रखने पर:![]()
![]()
![]()
उत्तर: वह भिन्न ![]() है।
है।
प्र.36. दो अंकों की संख्या के अंकों का योग 9 है। इस संख्या का नौ गुना…
हल:
माना दहाई का अंक ![]() और इकाई का अंक
और इकाई का अंक ![]() है।
है।
संख्या = ![]()
अंकों को पलटने पर बनी संख्या = ![]()
(i) ![]()
(ii) ![]()
![]()
![]()
![]() का मान
का मान ![]() रखने पर:
रखने पर:![]()
![]()
उत्तर: वह संख्या ![]() है।
है।
प्र.37. एक नाव दस घंटे में धारा के प्रतिकूल 30 किमी…
हल:
माना नाव की स्थिर पानी में चाल ![]() किमी/घंटा है।
किमी/घंटा है।
माना धारा की चाल ![]() किमी/घंटा है।
किमी/घंटा है।
अनुकूल चाल = ![]()
प्रतिकूल चाल = ![]()
(समय = दूरी / चाल)
(i) ![]()
(ii) ![]()
माना ![]() और
और ![]()
(iii) ![]()
(iv) ![]()
समी. (iii) को 4 से और समी. (iv) को 3 से गुणा करने पर:![]()
![]()
घटाने पर: ![]()
![]() का मान (iii) में रखने पर:
का मान (iii) में रखने पर: ![]()
![]()
![]()
दोनों को जोड़ने पर: ![]()
![]()
उत्तर: नाव की स्थिर पानी में चाल = 8 किमी/घंटा, धारा की चाल = 3 किमी/घंटा।
प्र.38. ऋतु धारा के अनुकूल 2 घंटे में 20 किमी तैर सकती है…
हल:
माना ऋतु की स्थिर जल में तैरने की चाल ![]() किमी/घंटा है।
किमी/घंटा है।
माना धारा की चाल ![]() किमी/घंटा है।
किमी/घंटा है।
(चाल = दूरी / समय)
(i) अनुकूल: ![]()
(ii) प्रतिकूल: ![]()
दोनों समीकरणों को जोड़ने पर:![]()
![]()
उत्तर: स्थिर जल में तैरने की चाल = 6 किमी/घंटा, धारा की चाल = 4 किमी/घंटा।
प्र.39. हल करें: ![]() …
…
हल:
माना ![]() और
और ![]()
(i) ![]()
(ii) ![]()
समी. (i) को 2 से और (ii) को 3 से गुणा करने पर:![]()
![]()
घटाने पर: ![]()
![]()
![]()
![]()
उत्तर: ![]()
प्र.40. हल करें: ![]() …
…
हल:
माना ![]() और
और ![]()
(i) ![]()
(ii) ![]()
समी. (i) को 2 से गुणा करने पर: ![]()
इसमें से समी. (ii) घटाने पर: ![]()
![]()
![]()
![]()
![]()
उत्तर: ![]()
प्र.41. हल करें: ![]() ,
, ![]()
हल:
दोनों समीकरणों को ![]() से भाग देने पर:
से भाग देने पर:
(i) ![]()
(ii) ![]()
माना ![]() और
और ![]()
(iii) ![]()
(iv) ![]()
समी. (iv) में से (iii) घटाने पर:![]()
![]()
![]()
![]()
उत्तर: ![]()
प्र.42. विलोपन विधि से हल करें: ![]() …
…
हल:
(i) ![]() (6 से गुणा करने पर)
(6 से गुणा करने पर) ![]()
(ii) ![]() (3 से गुणा करने पर)
(3 से गुणा करने पर) ![]()
समी. (i) में से (ii) घटाने पर:![]()
![]()
![]() का मान (ii) में रखने पर:
का मान (ii) में रखने पर: ![]()
उत्तर: ![]()
प्र.43. प्रतिस्थापन विधि से हल करें: ![]() …
…
हल:
समीकरणों को 10 से गुणा करने पर:
(i) ![]()
(ii) ![]()
समी. (i) से: ![]()
![]() का मान समी. (ii) में रखने पर:
का मान समी. (ii) में रखने पर:![]()
![]()
![]()
![]()
![]()
उत्तर: ![]()
प्र.44. हल करें: ![]() …
…
हल:
(i) ![]() (6 से गुणा करने पर)
(6 से गुणा करने पर) ![]()
(ii) ![]() (6 से गुणा करने पर)
(6 से गुणा करने पर) ![]()
समी. (i) को 3 से और (ii) को 10 से गुणा करने पर:![]()
![]()
दोनों को जोड़ने पर: ![]()
![]() का मान (ii) में रखने पर:
का मान (ii) में रखने पर: ![]()
उत्तर: ![]()
प्र.45. रोमिला… 2 पेंसिल तथा 3 रबड़ खरीदीं…
हल:
माना 1 पेंसिल का मूल्य ![]() रु है और 1 रबड़ का मूल्य
रु है और 1 रबड़ का मूल्य ![]() रु है।
रु है।
बीजगणितीय रूप:
रोमिला: ![]()
सोनाली: ![]()
ज्यामितीय (ग्राफीय) रूप:
यहाँ ![]()
![]()
![]()
चूँकि ![]() है, इसलिए दोनों रेखाएँ संपाती (Coincident) हैं।
है, इसलिए दोनों रेखाएँ संपाती (Coincident) हैं।
प्र.46. दो रेल की पटरियाँ, समीकरणों ![]() और
और ![]() द्वारा निरूपित की गई हैं।
द्वारा निरूपित की गई हैं।
हल:
ज्यामितीय रूप:![]()
![]()
![]()
![]()
![]()
चूँकि ![]() है, इसलिए दोनों रेखाएँ (पटरियाँ) समान्तर (Parallel) हैं।
है, इसलिए दोनों रेखाएँ (पटरियाँ) समान्तर (Parallel) हैं।
प्र.47. आफ़ताब अपनी पुत्री से कहता है, ‘सात वर्ष पूर्व मैं तुमसे सात गुनी आयु का था…’
हल:
माना आफ़ताब की वर्तमान आयु ![]() वर्ष है।
वर्ष है।
माना उसकी पुत्री की वर्तमान आयु ![]() वर्ष है।
वर्ष है।
बीजगणितीय रूप:
(i) सात वर्ष पूर्व: ![]()
(ii) अब से 3 वर्ष बाद: ![]()
ज्यामितीय (ग्राफीय) रूप:
यहाँ ![]() और
और ![]()
चूँकि ![]() है, इसलिए रेखाएँ प्रतिच्छेदी (Intersecting) हैं।
है, इसलिए रेखाएँ प्रतिच्छेदी (Intersecting) हैं।