MP Board 10th Coordinate Geometry Question Bank : अध्याय-7: निर्देशांक ज्यामिति प्रश्न बैंक
अध्याय 7: निर्देशांक ज्यामिति
स्मरणीय बिंदु
- किसी बिन्दु की
 -अक्ष से दूरी उस बिन्दु का
-अक्ष से दूरी उस बिन्दु का  -निर्देशांक या भुज कहलाती है। किसी बिन्दु की
-निर्देशांक या भुज कहलाती है। किसी बिन्दु की  -अक्ष से दूरी उस बिन्दु का
-अक्ष से दूरी उस बिन्दु का  -निर्देशांक या कोटि कहलाती है।
-निर्देशांक या कोटि कहलाती है। - दो बिन्दुओं
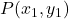 तथा
तथा 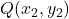 के बीच दूरी:
के बीच दूरी:![Rendered by QuickLaTeX.com \[PQ = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-09089e5171bbe091418814c9c0924525_l3.png)
- दो बिन्दुओं
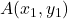 तथा
तथा 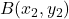 को जोड़ने वाले रेखाखण्ड को
को जोड़ने वाले रेखाखण्ड को 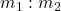 के अनुपात में विभाजित करने वाले बिन्दु
के अनुपात में विभाजित करने वाले बिन्दु 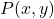 के निर्देशांक:
के निर्देशांक:![Rendered by QuickLaTeX.com \[P(x, y) = \left(\frac{m_1x_2 + m_2x_1}{m_1 + m_2}, \frac{m_1y_2 + m_2y_1}{m_1 + m_2}\right)\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-68efb8daaefeac9f69251d17c8cb563d_l3.png)
- रेखाखण्ड
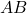 के मध्य-बिन्दु के निर्देशांक:
के मध्य-बिन्दु के निर्देशांक:![Rendered by QuickLaTeX.com \[(x, y) = \left(\frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2}\right)\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-517783d36c2d82d8603e7bbe09fa88a2_l3.png)
- यदि किसी त्रिभुज के शीर्षों के निर्देशांक
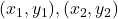 तथा
तथा 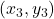 हैं तो उसके केन्द्रक के निर्देशांक:
हैं तो उसके केन्द्रक के निर्देशांक:![Rendered by QuickLaTeX.com \[\left(\frac{x_1 + x_2 + x_3}{3}, \frac{y_1 + y_2 + y_3}{3}\right)\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-d7c3bc220cac42a238c9439d0cbe577e_l3.png)
प्र.1 सही विकल्प चुनिए
1. मूल बिन्दु के निर्देशांक हैं:
(a) ![]() (b)
(b) ![]() (c)
(c) ![]() (d)
(d) ![]()
- हल: (d)
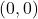
2. ![]() -अक्ष पर स्थित मूल बिन्दु से 4 इकाई की दूरी पर स्थित एक बिन्दु के निर्देशांक होंगें:
-अक्ष पर स्थित मूल बिन्दु से 4 इकाई की दूरी पर स्थित एक बिन्दु के निर्देशांक होंगें:
(a) ![]() (b)
(b) ![]() (c)
(c) ![]() (d)
(d) ![]()
- हल:
 -अक्ष पर
-अक्ष पर  -निर्देशांक 0 होता है, अतः बिन्दु
-निर्देशांक 0 होता है, अतः बिन्दु 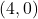 या
या 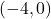 होगा। दिए गए विकल्पों में (b)
होगा। दिए गए विकल्पों में (b) 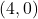 सही है।
सही है।
3. बिन्दुओं ![]() और
और ![]() के बीच की दूरी होगी:
के बीच की दूरी होगी:
(a) ![]()
(b) ![]()
(c) ![]()
(d) ![]()
- हल: (a)
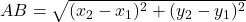 (यह मानक दूरी सूत्र है।)
(यह मानक दूरी सूत्र है।)
4. बिन्दु (8, 6) और (0, 0) के बीच की दूरी होगी:
(a) ![]() (b) 10 (c)
(b) 10 (c) ![]() (d)
(d) ![]()
- हल: दूरी =
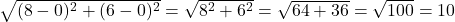 .
. - सही विकल्प: (b) 10
5. बिन्दुओं ![]() और
और ![]() को मिलाने वाली रेखा के मध्य-बिन्दु के निर्देशांक होंगें:
को मिलाने वाली रेखा के मध्य-बिन्दु के निर्देशांक होंगें:
(a) ![]()
(b) ![]()
(c) ![]()
(d) ![]()
- हल: (a)
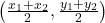 (यह मध्य-बिन्दु सूत्र है।)
(यह मध्य-बिन्दु सूत्र है।)
6. बिन्दुओं ![]() और
और ![]() को मिलाने वाली रेखा के मध्य-बिन्दु के निर्देशांक होंगें:
को मिलाने वाली रेखा के मध्य-बिन्दु के निर्देशांक होंगें:
(a) (2, 3) (b) (3, 2) (c) (0, 0) (d) (4, 4)
- हल:
 ;
;  .
. - सही विकल्प: (a) (2, 3)
7. यदि किसी बिन्दु P के निर्देशांक ![]() हैं तो
हैं तो ![]() को क्या कहते हैं?
को क्या कहते हैं?
(a) P का भुज (b) P की कोटि (c) ![]() के निर्देशांक (d) इनमें से कोई नहीं
के निर्देशांक (d) इनमें से कोई नहीं
- हल:
 -निर्देशांक को भुज कहते हैं।
-निर्देशांक को भुज कहते हैं। - सही विकल्प: (a) P का भुज
8. बिन्दु A (2, 3) की ![]() – अक्ष से दूरी है:
– अक्ष से दूरी है:
(a) 2 (b) 3 (c) 1 (d) 5
- हल:
 -अक्ष से दूरी
-अक्ष से दूरी  -निर्देशांक (भुज) के बराबर होती है।
-निर्देशांक (भुज) के बराबर होती है। - सही विकल्प: (a) 2
9. बिन्दुओं A (0, 6) और B (0, 2) के बीच की दूरी है:
(a) 6 (b) 8 (c) 4 (d) 2
- हल: दूरी =
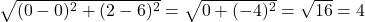 .
. - सही विकल्प: (c) 4
10. बिन्दु ![]() किस चतुर्थांश में स्थित है?
किस चतुर्थांश में स्थित है?
(a) प्रथम (b) द्वितीय (c) तृतीय (d) चतुर्थ
- हल:
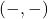 निर्देशांक तृतीय चतुर्थांश में होते हैं।
निर्देशांक तृतीय चतुर्थांश में होते हैं। - सही विकल्प: (c) तृतीय
11. बिन्दुओं ![]() और
और ![]() के बीच की दूरी है।
के बीच की दूरी है।
(a) 7 (b) ![]() (c)
(c) ![]() (d) 14
(d) 14
- हल: दूरी =
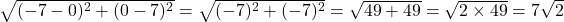 .
. - सही विकल्प: (b)
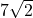
12. बिन्दु ![]() की
की ![]() – अक्ष से दूरी है:
– अक्ष से दूरी है:
(a) 2 (b) 3 (c) 1 (d) 5
- हल:
 -अक्ष से दूरी
-अक्ष से दूरी  -निर्देशांक (कोटि) के बराबर होती है।
-निर्देशांक (कोटि) के बराबर होती है। - सही विकल्प: (b) 3
13. ![]() – अक्ष पर प्रत्येक बिन्दु का
– अक्ष पर प्रत्येक बिन्दु का ![]() – निर्देशांक होता है:
– निर्देशांक होता है:
(a) 2 (b) 0 (c) 1 (d) इनमें से कोई नहीं
- हल:
 -अक्ष पर
-अक्ष पर  -निर्देशांक हमेशा 0 होता है।
-निर्देशांक हमेशा 0 होता है। - सही विकल्प: (b) 0
प्र.2 रिक्त स्थान की पूर्ति कीजिये
- एक वृत्त के व्यास के सिरों के निर्देशांक
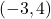 और
और 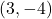 हैं। तब उसके केंद्र के निर्देशांक (0, 0) होंगें।
हैं। तब उसके केंद्र के निर्देशांक (0, 0) होंगें।
- हल: केंद्र व्यास का मध्य-बिन्दु होता है:
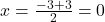 ;
; 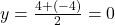 .
.
- हल: केंद्र व्यास का मध्य-बिन्दु होता है:
- बिन्दु (4, 5) प्रथम चतुर्थांश में स्थित है।
- यदि एक बिन्दु का
 -निर्देशांक 0 है तब वह
-निर्देशांक 0 है तब वह  -अक्ष पर स्थित होगा।
-अक्ष पर स्थित होगा।  -अक्ष और
-अक्ष और  -अक्ष का प्रतिच्छेद बिन्दु मूल बिन्दु कहलाता है।
-अक्ष का प्रतिच्छेद बिन्दु मूल बिन्दु कहलाता है।- बिन्दु
 में कोटि 3 है।
में कोटि 3 है। - बिन्दु
 में भुज -4 है।
में भुज -4 है। - किसी त्रिभुज के शीर्ष (4, 3), (2, -3) तथा (-3, 6) हैं। उसके केन्द्रक के निर्देशांक (1, 2) होंगें।
- हल:
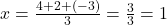 ;
; 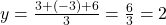 .
.
- हल:
- यदि एक बिन्दु का
 निर्देशांक 0 है तब वह
निर्देशांक 0 है तब वह  -अक्ष पर स्थित होगा।
-अक्ष पर स्थित होगा। - बिन्दु
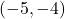 तृतीय चतुर्थांश में है।
तृतीय चतुर्थांश में है।
प्र.3 सही जोड़ी बनाइये
| स्तम्भ – अ | स्तम्भ – ब | सही जोड़ी |
|---|---|---|
| I. | (a) चतुर्थ | (d) |
| II. | (b) | (e) |
| III. बिन्दु | (c) | (a) चतुर्थ |
| IV. मूलबिन्दु के निर्देशांक | (d) | (b) |
| V. बिन्दु | (e) | (c) |
प्र.4 एक शब्द / वाक्य में उत्तर दीजिए
1. बिन्दु A(3, 4) की मूलबिन्दु से दूरी क्या होगी?
- उत्तर:
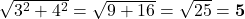
2. बिन्दु A(-1, 2) और B(3, -4) को मिलाने वाली रेखा के मध्य बिन्दु के निर्देशांक क्या होंगें?
- उत्तर:
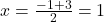 ;
; 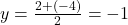 . (1, -1)
. (1, -1)
3. बिन्दुओं (-3, 4) और (2, 3) के बीच की दूरी क्या होगी?
- उत्तर:

4. बिन्दु A (-3, -4) की मूलबिन्दु से दूरी क्या होगी?
- उत्तर:
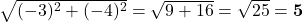
5. बिन्दु A (1, 2) और B (3, 4) को मिलाने वाली रेखा के मध्य बिन्दु के निर्देशांक क्या होंगें?
- उत्तर:
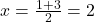 ;
; 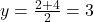 . (2, 3)
. (2, 3)
6. किसी त्रिभुज के शीर्षों के निर्देशांक (4, 3), (2, -3) तथा (-3, 5) है, उसके केन्द्रक निर्देशांक क्या होंगे?
- उत्तर:
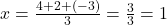 ;
; 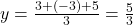 .
. 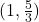
7. मूलबिन्दु से बिन्दु ![]() की दूरी लिखो।
की दूरी लिखो।
- उत्तर:
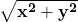
8. यदि त्रिभुज के शीर्ष निर्देशांक ![]() तथा
तथा ![]() हैं तो उसके केन्द्रक के निर्देशांक क्या होंगें?
हैं तो उसके केन्द्रक के निर्देशांक क्या होंगें?
- उत्तर:

9. मूल बिन्दु के निर्देशांक क्या हैं?
- उत्तर: (0, 0)
प्र.5 सत्य / असत्य लिखिए
- किसी बिन्दु का भुज शून्य है और कोटि 3 है तब वह
 -अक्ष पर स्थित होगा। (असत्य) (वह
-अक्ष पर स्थित होगा। (असत्य) (वह  -अक्ष पर स्थित होगा)
-अक्ष पर स्थित होगा)  -अक्ष पर मूलबिन्दु से 10 इकाई दूरी पर स्थित बिन्दु के निर्देशांक (10, 0) होंगें। (असत्य) (निर्देशांक
-अक्ष पर मूलबिन्दु से 10 इकाई दूरी पर स्थित बिन्दु के निर्देशांक (10, 0) होंगें। (असत्य) (निर्देशांक 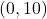 या
या 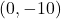 होंगे)
होंगे)- बिन्दु
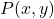 की मूलबिन्दु से दूरी
की मूलबिन्दु से दूरी 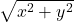 होती है। (सत्य)
होती है। (सत्य)  -अक्ष पर स्थित बिन्दु के निर्देशांक
-अक्ष पर स्थित बिन्दु के निर्देशांक 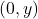 रूप के होते हैं। (सत्य)
रूप के होते हैं। (सत्य)- बिन्दु (1, 5) प्रथम चतुर्थांश में स्थित होगा। (सत्य)
- यदि किसी बिन्दु P के निर्देशांक (2, 5) हों तो 5 को P का भुज कहते हैं। (असत्य) (5 कोटि है, 2 भुज है)
- मूल बिन्दु से बिन्दु
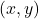 की
की 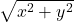 दूरी है। (सत्य)
दूरी है। (सत्य) - किसी बिन्दु का भुज शून्य है, तब वह
 -अक्ष पर स्थित होगा। (असत्य) (वह
-अक्ष पर स्थित होगा। (असत्य) (वह  -अक्ष पर स्थित होगा)
-अक्ष पर स्थित होगा) - किसी बिन्दु की कोटि शून्य है, तब वह
 -अक्ष पर स्थित होगा। (असत्य) (वह
-अक्ष पर स्थित होगा। (असत्य) (वह  -अक्ष पर स्थित होगा)
-अक्ष पर स्थित होगा) - मूलबिन्दु के निर्देशांक (0, 0) हैं। (सत्य)
- बिन्दु (-8, 6) द्वितीय चतुर्थांश में स्थित होगा। (सत्य)
- किसी बिन्दु की कोटि शून्य है तब वह
 -अक्ष पर स्थित होगा। (सत्य)
-अक्ष पर स्थित होगा। (सत्य) - किसी बिन्दु की भुज शून्य है, तब
 -वह अक्ष पर स्थित होगा। (सत्य)
-वह अक्ष पर स्थित होगा। (सत्य)
प्र.6. बिन्दुओं (0, 0) और (36, 15) के बीच की दूरी ज्ञात कीजिये।
- हल: दूरी सूत्र
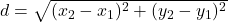 का उपयोग करने पर:
का उपयोग करने पर: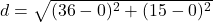
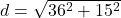
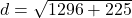
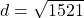
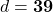
- उत्तर: 39
प्र.7. उस बिन्दु के निर्देशांक ज्ञात कीजिये जो बिन्दुओं (-1, 7) और (4, -3) को मिलाने वाले रेखाखण्ड को 2 : 3 के अनुपात में विभाजित करता है।
- हल: विभाजन सूत्र
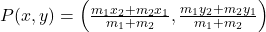 का उपयोग करने पर:
का उपयोग करने पर:
यहाँ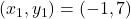 ,
, 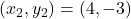 ,
,  ,
, 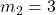
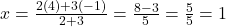
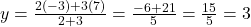
- उत्तर: बिन्दु (1, 3) है।
प्र.8. उस बिन्दु के निर्देशांक ज्ञात कीजिये जो बिन्दुओं (2, 5) और (-5, -2) को मिलाने वाले रेखाखण्ड को 3 : 4 अनुपात में विभाजित करता है।
- हल: विभाजन सूत्र का उपयोग करने पर:
यहाँ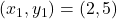 ,
, 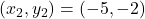 ,
, 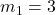 ,
, 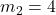
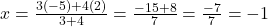
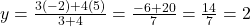
- उत्तर: बिन्दु (-1, 2) है।
प्र.9. त्रिभुज का केन्द्रक ज्ञात कीजिये जिसके शीर्ष (1, 4), (-1, -1), (3, -2) हैं।
- हल: केन्द्रक सूत्र
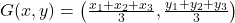 का उपयोग करने पर:
का उपयोग करने पर: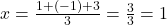
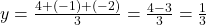
- उत्तर: केन्द्रक (1, 1/3) है।
प्र.10. वृत्त के केन्द्र के निर्देशांक ज्ञात कीजिये यदि उसके व्यास के सिरे के निर्देशांक (-3, 4) एवं (-5, 6) हैं।
- हल: वृत्त का केंद्र व्यास का मध्य-बिंदु होता है।
मध्य-बिंदु सूत्र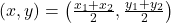 का उपयोग करने पर:
का उपयोग करने पर: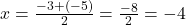
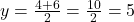
- उत्तर: केन्द्र (-4, 5) है।
प्र.11. किसी रेखाखण्ड के मध्यबिन्दु के निर्देशांक ज्ञात कीजिये यदि उसके सिरे के निर्देशांक (-9, 8) एवं (5, -7) हैं।
- हल: मध्य-बिंदु सूत्र का उपयोग करने पर:
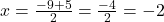
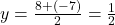
- उत्तर: मध्य-बिन्दु (-2, 1/2) है।
प्र.12. बिन्दुओं (2, 3) और (4, 1) के बीच की दूरी ज्ञात कीजिए।
- हल:
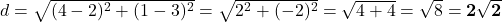
- उत्तर:
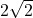
प्र.13. बिन्दुओं (-5, 7) और (-1, 3) के बीच की दूरी ज्ञात कीजिए।
- हल:
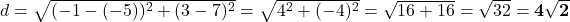
- उत्तर:

प्र.14. बिन्दुओं ![]() और
और ![]() के बीच की दूरी ज्ञात कीजिए।
के बीच की दूरी ज्ञात कीजिए।
- हल:
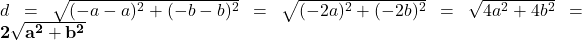
- उत्तर:
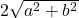
प्र.15. ![]() और
और ![]() में एक संबंध ज्ञात कीजिए, ताकि बिन्दु
में एक संबंध ज्ञात कीजिए, ताकि बिन्दु ![]() बिन्दुओं (7, 1) और (3, 5) से समदूरस्थ हो।
बिन्दुओं (7, 1) और (3, 5) से समदूरस्थ हो।
- हल:
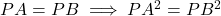

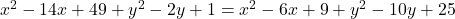
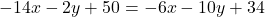
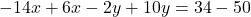
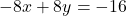
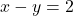 (दोनों पक्षों को -8 से भाग देने पर)
(दोनों पक्षों को -8 से भाग देने पर) - उत्तर:
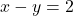
प्र.16. ![]() और
और ![]() में एक संबंध ज्ञात कीजिए, ताकि बिन्दु
में एक संबंध ज्ञात कीजिए, ताकि बिन्दु ![]() बिन्दुओं (3, 6) और (-3, 4) से समदूरस्थ हो।
बिन्दुओं (3, 6) और (-3, 4) से समदूरस्थ हो।
- हल:
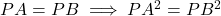
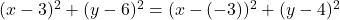
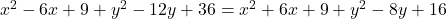
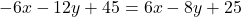

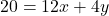
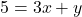 (दोनों पक्षों को 4 से भाग देने पर)
(दोनों पक्षों को 4 से भाग देने पर) - उत्तर:
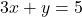
प्र.17. क्या बिन्दु (3, 2), (-2, -3) और (2, 3) एक त्रिभुज के शीर्ष हैं? यदि हाँ, तो बताइये कि किस प्रकार का त्रिभुज बनता है।
- हल:
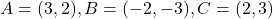
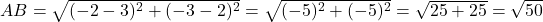
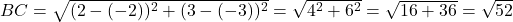
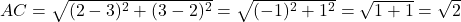
चूँकि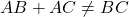 (
( 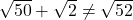 ), बिन्दु संरेख नहीं हैं, अतः वे त्रिभुज बनाते हैं।
), बिन्दु संरेख नहीं हैं, अतः वे त्रिभुज बनाते हैं।
पाइथागोरस प्रमेय की जाँच: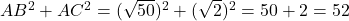
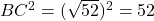
चूँकि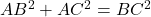 है।
है। - उत्तर: हाँ, यह एक समकोण त्रिभुज है।
प्र.18. जांच कीजिये कि क्या बिन्दु (5, -2), (6, 4) और (7, -2) एक समद्विबाहु त्रिभुज के शीर्ष हैं।
- हल:
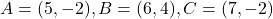
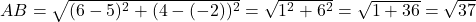
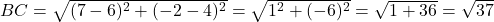
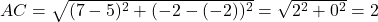
चूँकि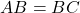 है।
है। - उत्तर: हाँ, यह एक समद्विबाहु त्रिभुज है।
प्र.19. यदि बिन्दु ![]() और
और ![]() एक समांतर चतुर्भुज के शीर्ष इसी क्रम में हों तो
एक समांतर चतुर्भुज के शीर्ष इसी क्रम में हों तो ![]() का मान ज्ञात कीजिए।
का मान ज्ञात कीजिए।
- हल: समांतर चतुर्भुज के विकर्ण एक दूसरे को समद्विभाजित करते हैं (Midpoint of
 = Midpoint of
= Midpoint of 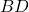 )
) का मध्य-बिन्दु:
का मध्य-बिन्दु: 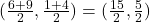
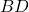 का मध्य-बिन्दु:
का मध्य-बिन्दु: 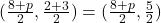
 -निर्देशांकों की तुलना करने पर:
-निर्देशांकों की तुलना करने पर: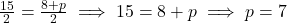
- उत्तर:

प्र.20. वह अनुपात ज्ञात कीजिये जिसमें बिन्दुओं A(1, -5) और B(-4, 5) को मिलाने वाला रेखाखण्ड ![]() -अक्ष से विभाजित होता है।
-अक्ष से विभाजित होता है।
- हल:
 -अक्ष पर
-अक्ष पर  -निर्देशांक 0 होता है। माना अनुपात
-निर्देशांक 0 होता है। माना अनुपात 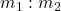 है।
है।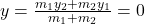
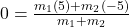
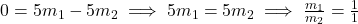
- उत्तर: अनुपात 1:1 है।
प्र.21. बिन्दु A के निर्देशांक ज्ञात कीजिये जहाँ AB एक वृत्त का व्यास है। जिसका केन्द्र (2, -3) है तथा B के निर्देशांक (1, 4) हैं।
- हल: केंद्र (O) व्यास (AB) का मध्य-बिंदु होता है। माना
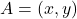
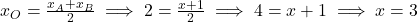
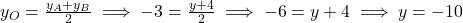
- उत्तर: A = (3, -10)
प्र.22. ![]() का वह मान ज्ञात कीजिये जिसके लिये बिन्दु P(2, -3) और Q(10,
का वह मान ज्ञात कीजिये जिसके लिये बिन्दु P(2, -3) और Q(10, ![]() ) के बीच की दूरी 10 मात्रक है।
) के बीच की दूरी 10 मात्रक है।
- हल:
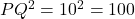
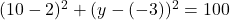
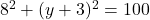
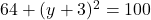
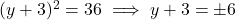
 या
या 
- उत्तर:
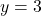 या
या 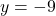
प्र.23. यदि बिन्दु C(1, -2) रेखाखण्ड A(2, 5) तथा B को मिलाने वाले रेखाखण्ड को 3 : 4 में विभाजित करता है, तो B के निर्देशांक ज्ञात करो।
- हल: यहाँ C विभाजक बिंदु है।
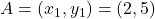 ,
, 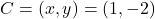 ,
, 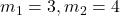 . माना
. माना 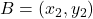
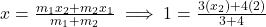
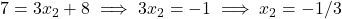

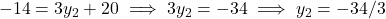
- उत्तर: B = (-1/3, -34/3)
प्र.24. बिन्दुओं A(2, -2) और B(-7, 4) को जोड़ने वाले रेखाखण्ड को समत्रिभाजित करने वाले बिन्दुओं के निर्देशांक ज्ञात कीजिये।
- हल: समत्रिभाजित (Trisect) करने वाले बिंदु
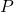 (1:2) और
(1:2) और 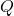 (2:1) होते हैं।
(2:1) होते हैं।
- बिंदु P (अनुपात 1:2):
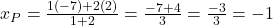
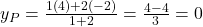
- बिंदु Q (अनुपात 2:1):
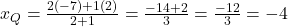
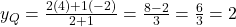
- बिंदु P (अनुपात 1:2):
- उत्तर: (-1, 0) और (-4, 2)
प्र.25. बिन्दुओं A(-2, 2) तथा B(2, 8) को जोड़ने वाले रेखाखण्ड AB को चार बराबर भागों में विभाजित करने वाले बिन्दुओं के निर्देशांक ज्ञात कीजिये।
- हल: हमें 3 बिंदु
 ज्ञात करने हैं।
ज्ञात करने हैं। 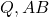 का मध्य-बिंदु होगा।
का मध्य-बिंदु होगा। 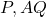 का मध्य-बिंदु होगा।
का मध्य-बिंदु होगा।  का मध्य-बिंदु होगा।
का मध्य-बिंदु होगा।
- Q (AB का मध्य-बिंदु):
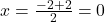 ,
, 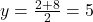 . Q = (0, 5)
. Q = (0, 5) - P (AQ का मध्य-बिंदु):
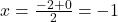 ,
, 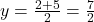 . P = (-1, 3.5)
. P = (-1, 3.5) - R (QB का मध्य-बिंदु):
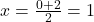 ,
, 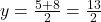 . R = (1, 6.5)
. R = (1, 6.5)
- Q (AB का मध्य-बिंदु):
- उत्तर: (-1, 3.5), (0, 5) और (1, 6.5)
प्र.26. यदि बिन्दु A(-2, -1), B(1, 0), C(![]() , 3) तथा D(1,
, 3) तथा D(1, ![]() ) समांतर चतुर्भुज के निर्देशांक हों तो
) समांतर चतुर्भुज के निर्देशांक हों तो ![]() और
और ![]() के मान ज्ञात कीजिये।
के मान ज्ञात कीजिये।
- हल: Midpoint of
 = Midpoint of
= Midpoint of 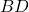
 का मध्य-बिन्दु:
का मध्य-बिन्दु: 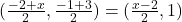
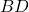 का मध्य-बिन्दु:
का मध्य-बिन्दु: 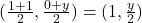
निर्देशांकों की तुलना करने पर: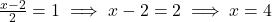

- उत्तर:
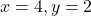
प्र.27. ![]() -अक्ष के किसी बिन्दु के निर्देशांक ज्ञात करो जो बिन्दु A(6, 5) तथा B(-4, 3) से समदूरस्थ हो।
-अक्ष के किसी बिन्दु के निर्देशांक ज्ञात करो जो बिन्दु A(6, 5) तथा B(-4, 3) से समदूरस्थ हो।
- हल:
 -अक्ष पर बिंदु
-अक्ष पर बिंदु 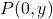 होता है।
होता है। 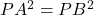
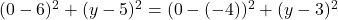
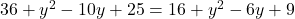
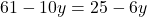
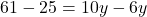

- उत्तर: (0, 9)
प्र.28. यदि Q(0, 1) बिन्दुओं P(5, -2) और R(![]() , 6) से समदूरस्थ है तो
, 6) से समदूरस्थ है तो ![]() के मान ज्ञात कीजिये। दूरियाँ QR और PR भी ज्ञात कीजिये।
के मान ज्ञात कीजिये। दूरियाँ QR और PR भी ज्ञात कीजिये।
- हल:

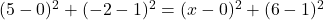
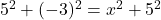
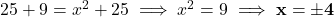 (नोट: प्रश्न P(5,-3) होना चाहिए, लेकिन छवि में P(5,-2) है।
(नोट: प्रश्न P(5,-3) होना चाहिए, लेकिन छवि में P(5,-2) है। 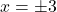 पाने के लिए, P(5,-2) का उपयोग करने पर:
पाने के लिए, P(5,-2) का उपयोग करने पर: 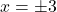 ) छवि P(5,-2) के अनुसार हल:
) छवि P(5,-2) के अनुसार हल: 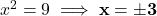 .
.
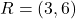 या
या 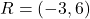 .
.- QR:
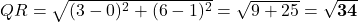 . (दोनों
. (दोनों  मानों के लिए)
मानों के लिए) - PR (जब R=(3, 6)):
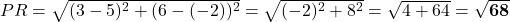
- PR (जब R=(-3, 6)):
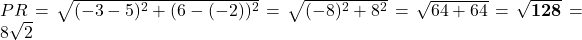
प्र.29. यदि बिन्दु (1, 2), (4, ![]() ), (
), (![]() , 6) और (3, 5) इसी क्रम में लेने पर, एक समांतर चतुर्भुज के शीर्ष हों तो
, 6) और (3, 5) इसी क्रम में लेने पर, एक समांतर चतुर्भुज के शीर्ष हों तो ![]() और
और ![]() ज्ञात कीजिये।
ज्ञात कीजिये।
- हल:
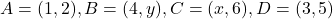
Midpoint of = Midpoint of
= Midpoint of 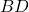
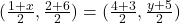
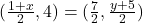
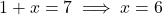
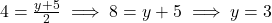
- उत्तर:
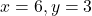
प्र.30. दर्शाईए कि बिन्दु (1, 7), (4, 2), (-1, -1) और (-4, 4) एक वर्ग के शीर्ष हैं।
- हल:
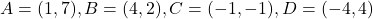
- भुजाएँ:
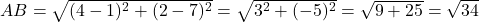
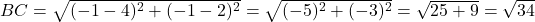
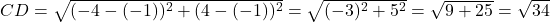

(चारों भुजाएँ बराबर हैं) - विकर्ण:
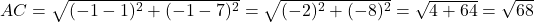
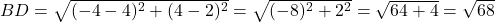
(दोनों विकर्ण बराबर हैं)
- भुजाएँ:
- उत्तर: चूँकि चारों भुजाएँ (
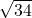 ) बराबर हैं और दोनों विकर्ण (
) बराबर हैं और दोनों विकर्ण ( ) बराबर हैं, यह एक वर्ग है। (इति सिद्धम)
) बराबर हैं, यह एक वर्ग है। (इति सिद्धम)