MP Board 10th Arithmetic Progression Question Bank : अध्याय-5: समांतर श्रेढ़ियाँ प्रश्न बैंक
अध्याय 5: समांतर श्रेणी
स्मरणीय बिंदु
- एक समांतर श्रेणी (Arithmetic Progression) संख्याओं की एक ऐसी सूची है जिसमें प्रत्येक पद (पहले पद के अतिरिक्त) अपने पद में एक निश्चित संख्या जोड़ने पर प्राप्त होता है। यह निश्चित संख्या सार्व अंतर कहलाती है।
- किसी समांतर श्रेणी (A.P.) में सार्व अंतर धनात्मक, ऋणात्मक या शून्य हो सकता है।
- व्यापक समांतर श्रेणी (A.P.):
 , जहाँ
, जहाँ  पहला पद और
पहला पद और  सार्व अंतर है।
सार्व अंतर है। - ऐसी समांतर श्रेणी जिसमें पदों की संख्या सीमित होती है, परिमित समांतर श्रेणी कहलाती है।
- ऐसी समांतर श्रेणी जिसमें पदों की संख्या असीमित होती है, अपरिमित समांतर श्रेणी कहलाती है।
- समांतर श्रेणी (A.P.):
 , का व्यापक पद
, का व्यापक पद  है।
है। - समांतर श्रेणी (A.P.):
 , में पदों की संख्या यदि
, में पदों की संख्या यदि  है तो श्रेणी का अंतिम पद
है तो श्रेणी का अंतिम पद  है।
है। - समांतर श्रेणी (A.P.):
 , के प्रथम
, के प्रथम  पदों का योग
पदों का योग ![Rendered by QuickLaTeX.com S_n = \frac{n}{2}[2a + (n-1)d]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-91f9edcdadf164b00530a88036211226_l3.png) है।
है। - समांतर श्रेणी (A.P.):
 , में पदों की संख्या यदि
, में पदों की संख्या यदि  है तो श्रेणी के
है तो श्रेणी के  पदों का योग
पदों का योग ![Rendered by QuickLaTeX.com S_n = \frac{n}{2}[a + l]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-52026dd5cf955cb173b4f87774680771_l3.png) है।
है।
प्र.1 सही विकल्प चुनिए।
1. A.P.: ![]() के लिए प्रथम पद एवं सार्व-अंतर क्रमशः हैं:
के लिए प्रथम पद एवं सार्व-अंतर क्रमशः हैं:
- हल: प्रथम पद (
 ) =
) = 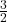
सार्व-अंतर ( ) =
) = 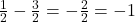
- सही विकल्प: (C)

2. A.P.: ![]() का 30 वां पद है:
का 30 वां पद है:
- हल:
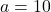 ,
, 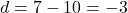 ,
, 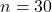

- सही विकल्प: (C) -77
3. A.P.: ![]() का 11 वां पद है:
का 11 वां पद है:
- हल:
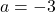 ,
, 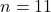
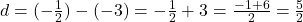
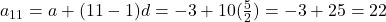
- सही विकल्प: (B) 22
4. ![]() का कौनसा पद 27 है:
का कौनसा पद 27 है:
- हल:
 ,
, 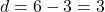 ,
, 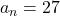
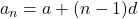

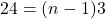
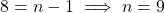
- सही विकल्प: (C) नवां
5. ![]() का 11 वां पद है:
का 11 वां पद है:
- हल:
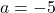 ,
, 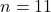
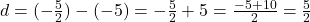

- सही विकल्प: (B) 20
6. समांतर श्रेणी ![]() का सार्व-अंतर है –
का सार्व-अंतर है –
- हल:
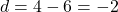
- सही विकल्प: (C) -2
7. समांतर श्रेणी ![]() का 5 वां पद है:
का 5 वां पद है:
- हल:
 ,
,  ,
, 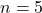
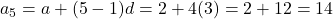
- सही विकल्प: (B) 14
8. किसी श्रेणी का प्रथम पद 7 तथा सार्व-अंतर -2 हो तो प्रथम चार पद होंगे –
- हल:
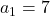 ,
, 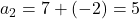 ,
, 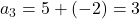 ,
, 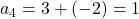
- सही विकल्प: (A) 7,5,3,1
9. समांतर श्रेणी में ![]() तब
तब ![]() है:
है:
- हल:
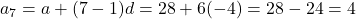
- सही विकल्प: (A) 4
10. श्रेणी ![]() का प्रथम पद एवं सार्व-अंतर है:
का प्रथम पद एवं सार्व-अंतर है:
- हल: प्रथम पद (
 ) = 3
) = 3
सार्व-अंतर ( ) =
) = 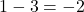
- सही विकल्प: (C) 3 और -2
11. 3 के गुणज प्रथम पाँच पदों का योगफल है:
- हल: श्रेणी है
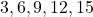 .
.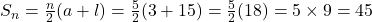
- सही विकल्प: (A) 45
12. समांतर श्रेणी ![]() का 10 वां पद :
का 10 वां पद :
- हल:
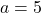 ,
,  ,
, 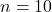
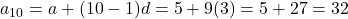
- सही विकल्प: (C) 32
13. समांतर श्रेणी का सार्व-अंतर ज्ञात कीजिए जबकि ![]() हो:
हो:
- हल:
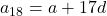
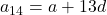
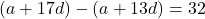
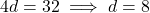
- सही विकल्प: (A) 8
प्र.2 रिक्त स्थान की पूर्ति कीजिए।
- समांतर श्रेणी
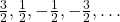 में सार्वअंतर
में सार्वअंतर  -1 है।
-1 है। - यदि किसी समांतर श्रेणी का
 वां पद
वां पद 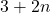 हो तब श्रेणी का प्रथम पद 5 होगा। (हल:
हो तब श्रेणी का प्रथम पद 5 होगा। (हल: 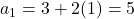 )
) - समांतर श्रेणी का प्रथम पद
 तथा सार्व-अंतर
तथा सार्व-अंतर  हो तो उसका दसवां पद
हो तो उसका दसवां पद 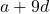 होगा।
होगा। - यदि
 समांतर श्रेणी में हैं, तब
समांतर श्रेणी में हैं, तब  को
को  और
और  का समांतर माध्य कहते हैं।
का समांतर माध्य कहते हैं।  पदों वाली समांतर श्रेणी का प्रथम पद
पदों वाली समांतर श्रेणी का प्रथम पद  तथा अंतिम पद
तथा अंतिम पद  हो, तो श्रेणी का योगफल
हो, तो श्रेणी का योगफल 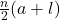 होता है।
होता है।- समांतर श्रेणी के कोई दो लगातार पदों का अन्तर सार्व-अंतर कहलाता है।
- 9 और 7 का समांतर माध्य 8 होता है। (हल:
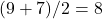 )
) - समांतर श्रेणी
 का सार्व-अंतर
का सार्व-अंतर 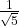 है। (हल:
है। (हल:  )
) - श्रेणी
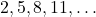 का 8 वां पद 23 है। (हल:
का 8 वां पद 23 है। (हल: 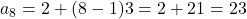 )
) - समांतर श्रेणी
 का अगला पद
का अगला पद 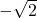 है। (हल:
है। (हल: 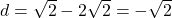 ,
, 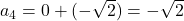 )
) - समांतर श्रेणी में
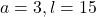 हो तो 5 पदों का योग 45 होगा। (हल:
हो तो 5 पदों का योग 45 होगा। (हल: 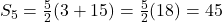 )
) - समांतर श्रेणी में
 तथा
तथा  हो तो सार्व-अंतर
हो तो सार्व-अंतर 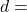 2 होगा। (हल:
2 होगा। (हल:  )
)
यहाँ सभी छवियों में दिए गए समांतर श्रेणी (A.P.) के प्रश्नों के हल दिए गए हैं:
प्र.3 सही जोड़ी बनाइए
| स्तम्भ – A | स्तम्भ – B |
|---|---|
| (i) व्यापक समांतर श्रेणी (A.P.) | (b) |
| (ii) ऐसी समांतर श्रेणी जिसमें पदों की संख्या सीमित हो | (c) परिमित समांतर श्रेणी |
| (iii) ऐसी समांतर श्रेणी जिसमें पदों की संख्या असीमित हो | (a) अपरिमित समांतर श्रेणी |
| (iv) समांतर श्रेणी का | (e) |
| (v) समांतर श्रेणी के | (d) |
प्र.4 एक शब्द / वाक्य में उत्तर दीजिए
- A.P.: 2, 7, 12, … के 10 वें पद का मान:
- यहाँ
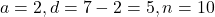
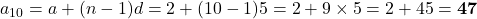
- यहाँ
- A.P.: 4, 6, 8, …, 40 में पदों की संख्या:
- यहाँ
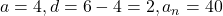

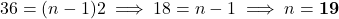
- यहाँ
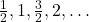 समांतर श्रेणी है या नहीं?
समांतर श्रेणी है या नहीं?
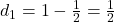 ;
; 
- चूंकि सार्व-अंतर समान है, हाँ, यह एक समांतर श्रेणी है।
- 4, 0, -4 का अगला पद क्या होगा?
- यहाँ
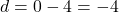
- अगला पद =
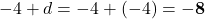
- यहाँ
- -2, 4, 10 का सार्व-अंतर क्या होगा?
- यदि किसी श्रेणी के पदों की संख्या सीमित न हो तो उसे क्या कहते हैं?
- अपरिमित श्रेणी (Aparimit Shreni)
- 5, 10, 15… के 8 पदों का योग क्या होगा?
- यहाँ
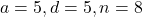
![Rendered by QuickLaTeX.com S_8 = \frac{n}{2}[2a + (n - 1)d] = \frac{8}{2}[2(5) + (8 - 1)5] = 4[10 + 7 \times 5] = 4[10 + 35] = 4[45] = \mathbf{180}](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-4f316e88ac8ddb03947ff79424419c61_l3.png)
- यहाँ
- -1, -2, -3 का 6 वां पद लिखिए।
- यहाँ
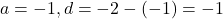
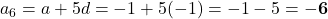
- यहाँ
प्र.5 सत्य / असत्य लिखिए
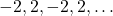 एक समांतर श्रेणी है। (असत्य)
एक समांतर श्रेणी है। (असत्य)- यदि
 A.P. में हैं तब
A.P. में हैं तब  है। (सत्य)
है। (सत्य) - श्रेणी 8, 6, 4, … का 6वाँ पद -2 है। (सत्य) (हल:
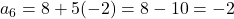 )
) 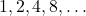 समांतर श्रेणी है। (असत्य) (यह गुणोत्तर श्रेणी है)
समांतर श्रेणी है। (असत्य) (यह गुणोत्तर श्रेणी है)- 3 और 5 का समांतर माध्य 4 है। (सत्य) (हल:
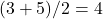 )
) - समांतर श्रेणी के
 पदों का योगफल
पदों का योगफल  होता है। (असत्य) (यह
होता है। (असत्य) (यह  वें पद का सूत्र है)
वें पद का सूत्र है) - यदि
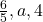 समांतर श्रेणी है, तो
समांतर श्रेणी है, तो  का मान
का मान  होगा। (सत्य) (हल:
होगा। (सत्य) (हल: 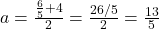 )
) 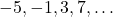 का सार्व-अंतर 6 होगा। (असत्य) (सार्व-अंतर 4 है)
का सार्व-अंतर 6 होगा। (असत्य) (सार्व-अंतर 4 है)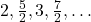 समांतर श्रेणी है। (सत्य) (सार्व-अंतर
समांतर श्रेणी है। (सत्य) (सार्व-अंतर 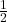 है)
है)- समांतर श्रेणी के पदों का योगफल
![Rendered by QuickLaTeX.com S_n = \frac{n}{2}[2a+(n-1)d]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-b3142ff70d8b3457a70bd297493c2c37_l3.png) है। (सत्य)
है। (सत्य)
विविध प्रश्न (प्र.6 से प्र.43)
प्र.6 ![]() का प्रथम पद
का प्रथम पद ![]() एवं सार्व-अंतर
एवं सार्व-अंतर ![]() है।
है।
प्र.7 ![]() और
और ![]() हो तो अगले चार पद:
हो तो अगले चार पद:
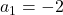
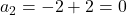
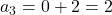
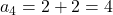
- उत्तर: -2, 0, 2, 4
प्र.8 A.P. ![]() का 10 वां पद:
का 10 वां पद:
प्र.9 5 के प्रथम 10 गुणजों का योग (A.P.: 5, 10, …, 50):
प्र.10 A.P. ![]() का 6वाँ पद:
का 6वाँ पद:
प्र.11 5 से विभाज्य प्रथम 10 धनात्मक पूर्णांकों का योग: (यह प्र.9 के समान है)
- A.P.: 5, 10, …, 50.
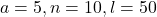 .
. 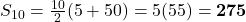
प्र.12 A.P. ![]() के 10 पदों तक योग:
के 10 पदों तक योग:
प्र.13 ![]() समांतर श्रेणी में हैं तो A का मान:
समांतर श्रेणी में हैं तो A का मान:
प्र.14 17 वां पद 10 वें पद से 7 अधिक है (![]() ):
):
प्र.15 A.P. का ![]() और
और ![]() :
:
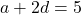 (1)
(1)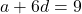 (2)
(2)- (2) – (1) करने पर:

 का मान (1) में रखने पर:
का मान (1) में रखने पर: 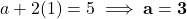
प्र.16 श्रेणी ![]() में कितने पद हैं?
में कितने पद हैं?
प्र.17 ![]() हो तो प्रथम दो पद:
हो तो प्रथम दो पद:
प्र.18 तीन अंकों वाली कितनी संख्याएँ 7 से विभाज्य हैं?
- A.P.: 105, 112, …, 994
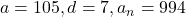

प्र.19 दो अंकों वाली कितनी संख्याएँ 3 से विभाज्य हैं?
- A.P.: 12, 15, …, 99
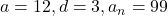
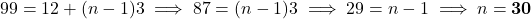
प्र.20 A.P. ![]() का कौनसा पद -81 है?
का कौनसा पद -81 है?
प्र.21 क्या ![]() का कोई पद 301 है?
का कोई पद 301 है?
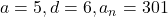
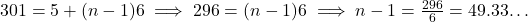
- उत्तर: नहीं, क्योंकि
 एक पूर्णांक नहीं है।
एक पूर्णांक नहीं है।
प्र.22 ![]() और
और ![]() है, कौनसा पद शून्य होगा?
है, कौनसा पद शून्य होगा?
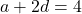 (1)
(1)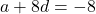 (2)
(2)- (2) – (1) करने पर:
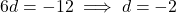
 का मान (1) में रखने पर:
का मान (1) में रखने पर: 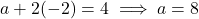
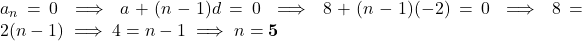
प्र.23 10 और 250 के बीच में 4 के कितने गुणज हैं?
- A.P.: 12, 16, …, 248
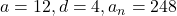
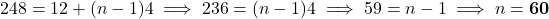
प्र.24 A.P. का ![]() और
और ![]() है,
है, ![]() ज्ञात कीजिए:
ज्ञात कीजिए:
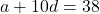 (1)
(1)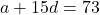 (2)
(2)- (2) – (1) करने पर:
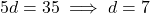
 का मान (1) में रखने पर:
का मान (1) में रखने पर: 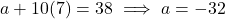
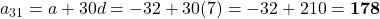
प्र.25 वह A.P. ज्ञात कीजिए जिसका ![]() और
और ![]() है:
है:
- (यह प्र.15 के समान है)
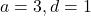
- A.P.: 3, 4, 5, 6, …
प्र.26 A.P. ![]() का कौनसा पद 78 होगा?
का कौनसा पद 78 होगा?
प्र.27 क्या A.P. ![]() का एक पद -150 है?
का एक पद -150 है?
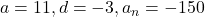
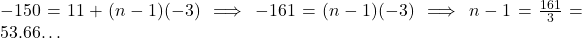
- उत्तर: नहीं, क्योंकि
 एक पूर्णांक नहीं है।
एक पूर्णांक नहीं है।
प्र.28 ![]() है,
है, ![]() और
और ![]() क्या है?
क्या है?
प्र.29 दो A.P. का ![]() समान है, 100वें पदों का अंतर 100 है, तो 1000वें पदों का अंतर:
समान है, 100वें पदों का अंतर 100 है, तो 1000वें पदों का अंतर:
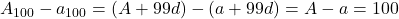
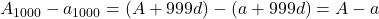
- उत्तर: 100
प्र.30 A.P. ![]() के कितने पद लिए जाएँ ताकि योग 78 हो?
के कितने पद लिए जाएँ ताकि योग 78 हो?
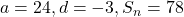
![Rendered by QuickLaTeX.com 78 = \frac{n}{2}[2(24) + (n - 1)(-3)] = \frac{n}{2}[48 - 3n + 3] = \frac{n}{2}[51 - 3n]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-2f4fb96beeab7acd1f2bf20902580c24_l3.png)
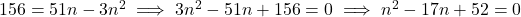
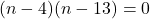
- उत्तर:
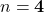 या
या 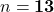 (दोनों मान संभव हैं)
(दोनों मान संभव हैं)
प्र.31 636 योग प्राप्त करने के लिए A.P. ![]() के कितने पद लेने चाहिए?
के कितने पद लेने चाहिए?
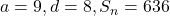
![Rendered by QuickLaTeX.com 636 = \frac{n}{2}[2(9) + (n - 1)8] = \frac{n}{2}[18 + 8n - 8] = \frac{n}{2}[10 + 8n] = n(5 + 4n)](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-6b7b13646ef49911199ac5af311e69b3_l3.png)
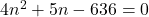
- द्विघाती सूत्र से:
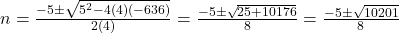
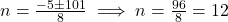 (ऋणात्मक मान संभव नहीं)
(ऋणात्मक मान संभव नहीं)- उत्तर:
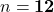
प्र.32 0 और 50 के बीच की विषम संख्याओं का योग:
- A.P.: 1, 3, 5, …, 49.
 .
. 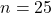 (कुल 25 विषम संख्याएँ हैं)
(कुल 25 विषम संख्याएँ हैं)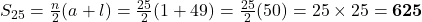
प्र.33 फूलों की क्यारी… 1ली पंक्ति में 23, …, अंतिम में 5. कुल कितनी पंक्तियाँ हैं?
- A.P.: 23, 21, 19, …, 5
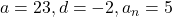
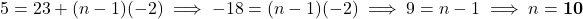
प्र.34 A.P. ज्ञात कीजिए जिसका ![]() और
और ![]() :
:

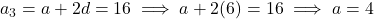
- A.P.: 4, 10, 16, 22, …
प्र.35 A.P. ![]() का अंतिम पद से 11वां पद:
का अंतिम पद से 11वां पद:
- A.P. को पलटें:
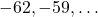
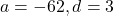
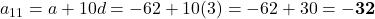
प्र.36 A.P. ![]() का कौनसा पद 54वें पद से 132 अधिक होगा?
का कौनसा पद 54वें पद से 132 अधिक होगा?
प्र.37 ![]() के किस मान के लिए A.P.
के किस मान के लिए A.P. ![]() और
और ![]() के nवें पद बराबर होंगे?
के nवें पद बराबर होंगे?
- A.P. 1:

- A.P. 2:
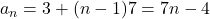
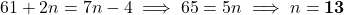
प्र.38 A.P. ![]() में अंतिम पद से 20 वां पद:
में अंतिम पद से 20 वां पद:
- A.P. को पलटें:
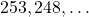
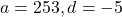
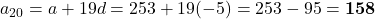
प्र.39 A.P. के ![]() और
और ![]() है,
है, ![]() ज्ञात कीजिए:
ज्ञात कीजिए:
प्र.40 प्रथम 100 धन पूर्णांकों का योग (A.P.: 1, 2, …, 100):
प्र.41 ![]() वाली सूची के प्रथम 24 पदों का योग:
वाली सूची के प्रथम 24 पदों का योग:
प्र.42 ![]() दिया है,
दिया है, ![]() और
और ![]() का मान:
का मान:
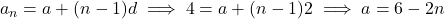 (1)
(1) (2)
(2)- (1) को (2) में रखने पर:
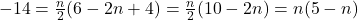
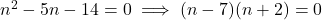
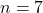 (
(  ऋणात्मक नहीं हो सकता)
ऋणात्मक नहीं हो सकता)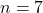 को (1) में रखने पर:
को (1) में रखने पर: 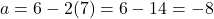
- उत्तर:
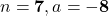
प्र.43 ![]() एवं
एवं ![]() के मान ज्ञात कीजिए जिसमें
के मान ज्ञात कीजिए जिसमें ![]() एक A.P. में हों:
एक A.P. में हों:
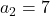 और
और