MP Board 10th Algebric method of solving a pair of linear equations : विषय “रैखिक समीकरण युग्म को हल करने की बीजीय विधि” का एक व्यवस्थित नोट है, जिसमें उदाहरण 7 और प्रतिस्थापन विधि के चरणों को समझाया गया है।
3.4 एक रैखिक समीकरण युग्म को हल करने की बीजीय विधि
पिछले अनुभाग में, हमने रैखिक समीकरण युग्म को हल करने के लिए ग्राफीय विधि का उपयोग किया।
बीजीय विधि की आवश्यकता क्यों है?
ग्राफीय विधि तब असुविधाजनक हो सकती है, जब हलों को निरूपित करने वाले बिंदुओं के निर्देशांक पूर्णांक (integer) न हों, जैसे ![]() या
या ![]() । इस प्रकार के बिंदुओं को ग्राफ पर सटीकता से पढ़ने में त्रुटि हो सकती है।
। इस प्रकार के बिंदुओं को ग्राफ पर सटीकता से पढ़ने में त्रुटि हो सकती है।
इसलिए, हम हल ज्ञात करने के लिए बीजीय विधियों का अध्ययन करेंगे।
3.4.1 प्रतिस्थापन विधि (Substitution Method)
इस विधि में, हम एक समीकरण से एक चर (variable) का मान दूसरे चर के पदों में व्यक्त करते हैं और उसे दूसरे समीकरण में प्रतिस्थापित (substitute) कर देते हैं।
उदाहरण 7
प्रश्न: प्रतिस्थापन विधि द्वारा निम्न रैखिक समीकरण युग्म को हल कीजिए:
![]() — (1)
— (1)
![]() — (2)
— (2)
हल:
चरण 1: किसी एक समीकरण को लें और किसी एक चर को दूसरे के पदों में लिखिए।
हम समीकरण (2) को लेते हैं, क्योंकि इससे ![]() का मान निकालना आसान है:
का मान निकालना आसान है:
![]()
![]() — (3)
— (3)
चरण 2: ![]() के इस मान को समीकरण (1) में प्रतिस्थापित (substitute) कीजिए।
के इस मान को समीकरण (1) में प्रतिस्थापित (substitute) कीजिए।
![]()
![]()
![]()
![]()
![]()
![]()
![]()
चरण 3: ![]() के इस मान को समीकरण (3) में प्रतिस्थापित करके
के इस मान को समीकरण (3) में प्रतिस्थापित करके ![]() का मान ज्ञात कीजिए।
का मान ज्ञात कीजिए।
![]()
![]()
![]()
![]()
![]()
![]()
अतः, हल है:
![]()
(सत्यापन: आप ![]() और
और ![]() के इन मानों को समीकरण (1) और (2) में रखकर जाँच कर सकते हैं कि दोनों समीकरण संतुष्ट होते हैं।)
के इन मानों को समीकरण (1) और (2) में रखकर जाँच कर सकते हैं कि दोनों समीकरण संतुष्ट होते हैं।)
प्रतिस्थापन विधि के चरण (सारांश)
- चरण 1: एक चर का मान (माना
 ) दूसरे चर (माना
) दूसरे चर (माना  ) के पदों में किसी भी एक समीकरण (जो सुविधाजनक हो) से ज्ञात कीजिए।
) के पदों में किसी भी एक समीकरण (जो सुविधाजनक हो) से ज्ञात कीजिए। - चरण 2:
 के इस मान को दूसरे समीकरण में प्रतिस्थापित कीजिए और इसे एक चर
के इस मान को दूसरे समीकरण में प्रतिस्थापित कीजिए और इसे एक चर  के समीकरण के रूप में बदलिए, जिसको हल किया जा सकता है।
के समीकरण के रूप में बदलिए, जिसको हल किया जा सकता है। - चरण 3: चरण 2 से प्राप्त
 के मान को, चरण 1 में प्रयोग किए गए समीकरण में प्रतिस्थापित करके, दूसरे चर
के मान को, चरण 1 में प्रयोग किए गए समीकरण में प्रतिस्थापित करके, दूसरे चर  का मान प्राप्त कीजिए।
का मान प्राप्त कीजिए।
प्रश्नावली 3.3 (हल)
1. निम्न रैखिक समीकरण युग्म को प्रतिस्थापन विधि से हल कीजिए:
(i)  और
और 
हल:
दिए गए समीकरण हैं:
![]()
![]()
चरण 1: समीकरण (2) से ![]() का मान
का मान ![]() के पदों में लिखने पर:
के पदों में लिखने पर:
![]()
चरण 2: ![]() के इस मान को समीकरण (1) में प्रतिस्थापित करने पर:
के इस मान को समीकरण (1) में प्रतिस्थापित करने पर:
![]()
![]()
![]()
![]()
![]()
चरण 3: ![]() के इस मान को समीकरण (3) में रखने पर:
के इस मान को समीकरण (3) में रखने पर:
![]()
![]()
अतः, हल है: ![]()
(ii) 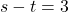 और
और 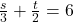
हल:
दिए गए समीकरण हैं:
![]()
![]()
चरण 1: समीकरण (1) से ![]() का मान
का मान ![]() के पदों में लिखने पर:
के पदों में लिखने पर:
![]()
चरण 2: ![]() के इस मान को समीकरण (2) में प्रतिस्थापित करने पर:
के इस मान को समीकरण (2) में प्रतिस्थापित करने पर:
![]()
समीकरण को सरल करने के लिए 6 से गुणा (LCM) करने पर:
![]()
![]()
![]()
![]()
![]()
चरण 3: ![]() के इस मान को समीकरण (3) में रखने पर:
के इस मान को समीकरण (3) में रखने पर:
![]()
![]()
अतः, हल है: ![]()
(iii) 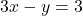 और
और 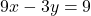
हल:
दिए गए समीकरण हैं:
![]()
![]()
चरण 1: समीकरण (1) से ![]() का मान
का मान ![]() के पदों में लिखने पर:
के पदों में लिखने पर:![]() — (3)
— (3)
चरण 2: ![]() के इस मान को समीकरण (2) में प्रतिस्थापित करने पर:
के इस मान को समीकरण (2) में प्रतिस्थापित करने पर:
![]()
![]()
![]()
यह कथन ![]() के सभी मानों के लिए सत्य है। इसका मतलब है कि इन समीकरणों का कोई अद्वितीय हल नहीं है, बल्कि ये रेखाएँ संपाती (Coincident) हैं।
के सभी मानों के लिए सत्य है। इसका मतलब है कि इन समीकरणों का कोई अद्वितीय हल नहीं है, बल्कि ये रेखाएँ संपाती (Coincident) हैं।
अतः, इस समीकरण युग्म के अपरिमित रूप से अनेक हल (infinitely many solutions) हैं।
(iv) 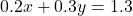 और
और 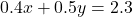
हल:
दशमलव (decimals) हटाने के लिए, हम दोनों समीकरणों को 10 से गुणा करते हैं:
![]()
![]()
चरण 1: समीकरण (1) से ![]() का मान
का मान ![]() के पदों में लिखने पर:
के पदों में लिखने पर:
![]()
![]() — (3)
— (3)
चरण 2: ![]() के इस मान को समीकरण (2) में प्रतिस्थापित करने पर:
के इस मान को समीकरण (2) में प्रतिस्थापित करने पर:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
चरण 3: ![]() के इस मान को समीकरण (3) में रखने पर:
के इस मान को समीकरण (3) में रखने पर:
![]()
![]()
![]()
![]()
अतः, हल है: ![]()
(v) 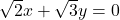 और
और 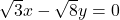
हल:
दिए गए समीकरण हैं:
![]()
![]()
चरण 1: समीकरण (1) से ![]() का मान
का मान ![]() के पदों में लिखने पर:
के पदों में लिखने पर:
![]()
![]() — (3)
— (3)
चरण 2: ![]() के इस मान को समीकरण (2) में प्रतिस्थापित करने पर:
के इस मान को समीकरण (2) में प्रतिस्थापित करने पर:
![Rendered by QuickLaTeX.com \[\sqrt{3}\left(\frac{-\sqrt{3}y}{\sqrt{2}}\right) - \sqrt{8}y = 0\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-238565de52d0d891d8d6bccce8ee07b8_l3.png)
![]()
![]() को कॉमन (common) लेने पर:
को कॉमन (common) लेने पर:
![]()
चूँकि ![]() है, इसलिए:
है, इसलिए:![]()
चरण 3: ![]() के इस मान को समीकरण (3) में रखने पर:
के इस मान को समीकरण (3) में रखने पर:
![]()
![]()
अतः, हल है: ![]()
(vi) 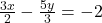 और
और 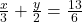
हल:
भिन्न (fractions) को हटाने के लिए, हम दोनों समीकरणों को उनके LCM से गुणा करके सरल करते हैं।
समीकरण (1) को 6 से गुणा करने पर:
![]()
![]() — (1a)
— (1a)
समीकरण (2) को 6 से गुणा करने पर:
![]()
![]() — (2a)
— (2a)
अब हम इन नए समीकरणों (1a) और (2a) को हल करते हैं।
चरण 1: समीकरण (2a) से ![]() का मान
का मान ![]() के पदों में लिखने पर:
के पदों में लिखने पर:
![]()
![]() — (3)
— (3)
चरण 2: ![]() के इस मान को समीकरण (1a) में प्रतिस्थापित करने पर:
के इस मान को समीकरण (1a) में प्रतिस्थापित करने पर:
![]()
समीकरण को 2 से गुणा करने पर:
![]()
![]()
![]()
![]()
![]()
चरण 3: ![]() के इस मान को समीकरण (3) में रखने पर:
के इस मान को समीकरण (3) में रखने पर:
![]()
![]()
![]()
![]()
अतः, हल है: ![]()
यहाँ प्रश्नावली 3.3 के प्रश्न 2 और 3 का संपूर्ण हल है, जिसे छात्र नोट्स के रूप में उपयोग कर सकते हैं।
प्रश्नावली 3.3 के हल
2.  का मान ज्ञात करना
का मान ज्ञात करना
प्रश्न: ![]() और
और ![]() को हल कीजिए और इससे
को हल कीजिए और इससे ![]() का वह मान ज्ञात कीजिए जिसके लिए
का वह मान ज्ञात कीजिए जिसके लिए ![]() हो।
हो।
हल:
भाग 1: समीकरणों को हल करना
दिए गए समीकरण हैं:
![]()
— (1)
![]()
— (2)
हम यहाँ विलोपन विधि (Elimination Method) का प्रयोग कर रहे हैं, क्योंकि ![]() पद दोनों में समान है।
पद दोनों में समान है।
समीकरण (1) में से समीकरण (2) को घटाने पर:
![]()
![]()
![]()
![]()
अब, ![]() का मान समीकरण (1) में रखने पर:
का मान समीकरण (1) में रखने पर:
![]()
![]()
![]()
![]()
![]()
अतः, समीकरणों का हल ![]() और
और ![]() है।
है।
भाग 2: ![]() का मान ज्ञात करना
का मान ज्ञात करना
हमें ![]() और
और ![]() के इन मानों को
के इन मानों को ![]() समीकरण में रखना है।
समीकरण में रखना है।
![]()
![]()
![]()
![]()
उत्तर: ![]() ,
, ![]() , और
, और ![]()
3. रैखिक समीकरण युग्म (प्रतिस्थापन विधि)
(i) दो संख्याओं का अंतर 26 है
प्रश्न: दो संख्याओं का अंतर 26 है और एक संख्या दूसरी संख्या की तीन गुनी है। उन्हें ज्ञात कीजिए।
हल:
- चरण 1 (समीकरण बनाना):
- माना पहली (बड़ी) संख्या =

- माना दूसरी (छोटी) संख्या =

- पहली शर्त (अंतर):
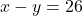 — (1)
— (1) - दूसरी शर्त (तीन गुनी):
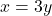 — (2)
— (2)
- माना पहली (बड़ी) संख्या =
- चरण 2 (प्रतिस्थापन):
- समीकरण (2) से
 का मान पहले से ही
का मान पहले से ही  के पदों में है। इसे समीकरण (1) में प्रतिस्थापित करने पर:
के पदों में है। इसे समीकरण (1) में प्रतिस्थापित करने पर: 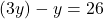
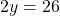
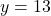
- समीकरण (2) से
- चरण 3 (मान ज्ञात करना):
 का मान समीकरण (2) में रखने पर:
का मान समीकरण (2) में रखने पर: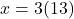
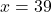
उत्तर: वे दो संख्याएँ 39 और 13 हैं।
(ii) दो संपूरक कोण
प्रश्न: दो संपूरक कोणों में बड़ा कोण छोटे कोण से 18 डिग्री अधिक है। उन्हें ज्ञात कीजिए।
हल:
- चरण 1 (समीकरण बनाना):
- माना बड़ा कोण =

- माना छोटा कोण =

- पहली शर्त (संपूरक):
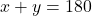 — (1)
— (1) - (क्योंकि संपूरक कोणों का योग 180° होता है)
- दूसरी शर्त (अंतर):
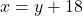 — (2)
— (2)
- माना बड़ा कोण =
- चरण 2 (प्रतिस्थापन):
- समीकरण (2) से
 का मान समीकरण (1) में प्रतिस्थापित करने पर:
का मान समीकरण (1) में प्रतिस्थापित करने पर: 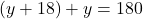
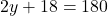
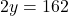
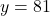
- समीकरण (2) से
- चरण 3 (मान ज्ञात करना):
 का मान समीकरण (2) में रखने पर:
का मान समीकरण (2) में रखने पर: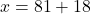
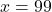
उत्तर: वे दो कोण 99° और 81° हैं।
(iii) क्रिकेट टीम (बल्ले और गेंद)
प्रश्न: एक क्रिकेट टीम के कोच ने 7 बल्ले तथा 6 गेंदें ₹ 3800 में खरीदीं। बाद में, उसने 3 बल्ले तथा 5 गेंदें ₹ 1750 में खरीदीं। प्रत्येक बल्ले और प्रत्येक गेंद का मूल्य ज्ञात कीजिए।
हल:
- चरण 1 (समीकरण बनाना):
- माना 1 बल्ले का मूल्य = ₹

- माना 1 गेंद का मूल्य = ₹

- पहली शर्त:
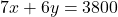 — (1)
— (1) - दूसरी शर्त:
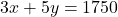 — (2)
— (2)
- माना 1 बल्ले का मूल्य = ₹
- चरण 2 (प्रतिस्थापन):
- समीकरण (2) से
 का मान
का मान  के पदों में लिखने पर:
के पदों में लिखने पर: 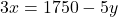
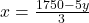 — (3)
— (3)- अब,
 के इस मान को समीकरण (1) में प्रतिस्थापित करने पर:
के इस मान को समीकरण (1) में प्रतिस्थापित करने पर: 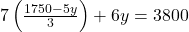
- भिन्न हटाने के लिए पूरे समीकरण को 3 से गुणा करने पर:
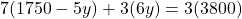
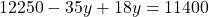
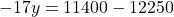
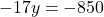
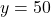
- समीकरण (2) से
- चरण 3 (मान ज्ञात करना):
 का मान समीकरण (3) में रखने पर:
का मान समीकरण (3) में रखने पर: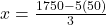
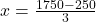
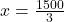
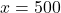
उत्तर: 1 बल्ले का मूल्य ₹ 500 और 1 गेंद का मूल्य ₹ 50 है।
(iv) टैक्सी का भाड़ा
प्रश्न: एक नगर में टैक्सी के भाड़े में एक नियत भाड़े के अतिरिक्त चली गई दूरी पर भाड़ा सम्मिलित किया जाता है। 10 km दूरी के लिए भाड़ा ₹ 105 है तथा 15 km के लिए भाड़ा ₹ 155 है। नियत भाड़ा तथा प्रति km भाड़ा क्या है? एक व्यक्ति को 25 km यात्रा करने के लिए कितना भाड़ा देना होगा?1
हल:
- चरण 1 (समीकरण बनाना):
- माना नियत भाड़ा (Fixed charge) = ₹

- माना प्रति km भाड़ा (Per km charge) = ₹

- पहली शर्त (10 km):
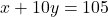 — (1)
— (1) - दूसरी शर्त (15 km):
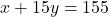 — (2)
— (2)
- माना नियत भाड़ा (Fixed charge) = ₹
- चरण 2 (प्रतिस्थापन):
- समीकरण (1) से
 का मान
का मान  के पदों में लिखने पर:
के पदों में लिखने पर: 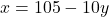 — (3)
— (3) के इस मान को समीकरण (2) में प्रतिस्थापित करने पर:
के इस मान को समीकरण (2) में प्रतिस्थापित करने पर: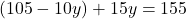
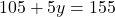
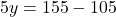
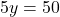
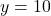
- समीकरण (1) से
- चरण 3 (मान ज्ञात करना):
 का मान समीकरण (3) में रखने पर:
का मान समीकरण (3) में रखने पर: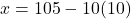
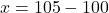
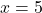
उत्तर (भाग 1): नियत भाड़ा ₹ 5 है और प्रति km भाड़ा ₹ 10 है।
25 km यात्रा के लिए भाड़ा:
- कुल भाड़ा =
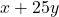
- कुल भाड़ा =
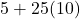
- कुल भाड़ा =
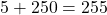
उत्तर (भाग 2): 25 km यात्रा के लिए ₹ 255 देना होगा।
(v) भिन्न (Fraction)
प्रश्न: यदि किसी भिन्न के अंश और हर दोनों में 2 जोड़ दिया जाए, तो वह ![]() हो जाती है। यदि अंश और हर दोनों में 3 जोड़ दिया जाए, तो वह
हो जाती है। यदि अंश और हर दोनों में 3 जोड़ दिया जाए, तो वह ![]() हो जाती है। वह भिन्न ज्ञात कीजिए।
हो जाती है। वह भिन्न ज्ञात कीजिए।
हल:
- चरण 1 (समीकरण बनाना):
- माना अंश (Numerator) =

- माना हर (Denominator) =

- मूल भिन्न =
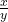
- पहली शर्त:
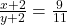
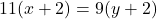
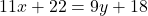
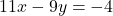 — (1)
— (1)
- दूसरी शर्त:
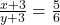
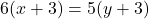
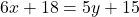
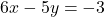 — (2)
— (2)
- माना अंश (Numerator) =
- चरण 2 (प्रतिस्थापन):
- समीकरण (2) से
 का मान
का मान  के पदों में लिखने पर:
के पदों में लिखने पर: 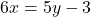
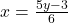 — (3)
— (3) के इस मान को समीकरण (1) में प्रतिस्थापित करने पर:
के इस मान को समीकरण (1) में प्रतिस्थापित करने पर: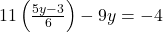
- समीकरण को 6 से गुणा करने पर:
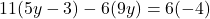
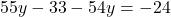
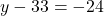
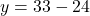
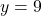
- समीकरण (2) से
- चरण 3 (मान ज्ञात करना):
 का मान समीकरण (3) में रखने पर:
का मान समीकरण (3) में रखने पर: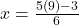
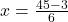
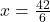
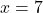
उत्तर: वह भिन्न ![]() है।
है।
(vi) जैकब की आयु
प्रश्न: पाँच वर्ष बाद जैकब की आयु उसके पुत्र की आयु से तीन गुनी हो जाएगी। पाँच वर्ष पूर्व जैकब की आयु उसके पुत्र की आयु की सात गुनी थी। उनकी वर्तमान आयु क्या है?
हल:
- चरण 1 (समीकरण बनाना):
- माना जैकब की वर्तमान आयु =
 वर्ष
वर्ष - माना उसके पुत्र की वर्तमान आयु =
 वर्ष
वर्ष - पहली शर्त (5 वर्ष बाद):
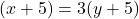
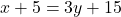
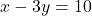 — (1)
— (1)
- दूसरी शर्त (5 वर्ष पूर्व):
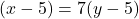
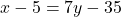
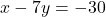 — (2)
— (2)
- माना जैकब की वर्तमान आयु =
- चरण 2 (प्रतिस्थापन):
- समीकरण (1) से
 का मान
का मान  के पदों में लिखने पर:
के पदों में लिखने पर: 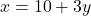 — (3)
— (3) के इस मान को समीकरण (2) में प्रतिस्थापित करने पर:
के इस मान को समीकरण (2) में प्रतिस्थापित करने पर:
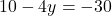
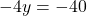
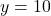
- समीकरण (1) से
- चरण 3 (मान ज्ञात करना):
 का मान समीकरण (3) में रखने पर:
का मान समीकरण (3) में रखने पर: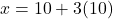
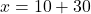
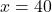
उत्तर: जैकब की वर्तमान आयु 40 वर्ष और उसके पुत्र की वर्तमान आयु 10 वर्ष है।