MP 12th Physics Continuous Charge Distribution : संतत आवेश वितरण

by

संतत आवेश वितरण Continuous Charge Distribution

MP 12th Physics Continuous Charge Distribution : अब तक हमने विविक्त आवेशों q1​,q2​,…,qn​ के आवेश विन्यास के विषय में चर्चा की है। इसका कारण यह है कि ऐसे विन्यासों के लिए गणितीय परिकलन सरल होते हैं जिनमें कलन (कैल्कुलस) की आवश्यकता नहीं होती। साथ ही, बहुत से कार्यों के लिए विविक्त आवेशों के पदों में कार्य करना व्यावहारिक नहीं होता और हमें संतत आवेश वितरण की आवश्यकता होती है। उदाहरणार्थ, किसी आवेशित चालक के पृष्ठ पर सूक्ष्म आवेशित अवयवों की अवस्थितियों के पदों में आवेश वितरण का विशेष रूप से उल्लेख करना व्यावहारिक नहीं है। चालक के पृष्ठ पर किसी क्षेत्रफ़ल अवयव ΔS (जो स्थूल स्तर पर बहुत छोटा परंतु इलेक्ट्रॉनों की विशाल संख्या को सम्मिलित करने के लिए पर्याप्त है) के विषय में विचार करके उस अवयव पर आवेश ΔQ का पृथक-पृथक उल्लेख करना अधिक उपयुक्त है। इसके बाद हम क्षेत्रफ़ल अवयव पर पृष्ठीय आवेश घनत्व σ की परिभाषा इस प्रकार करते हैं-

    \[\sigma = \frac{\Delta Q}{\Delta S} \qquad (1.23)\]

WhatsApp Channel Join Now
Telegram Channel Join Now

ऐसा हम चालक के पृष्ठ के विभिन्न बिंदुओं पर कर सकते हैं और इस प्रकार एक संतत फलन σ (जिसे पृष्ठीय आवेश घनत्व कहते हैं) पर पहुँचते हैं। इस रूप में वर्णित पृष्ठीय आवेश घनत्व σ आवेश की क्वांयटमता तथा सूक्ष्मदर्शीय स्तर पर आवेश की असंततता वितरण की उपेक्षा करता है। σ स्थूलदर्शीय रूप में पृष्ठीय आवेश घनत्व है जो एक प्रकार से, सूक्ष्मदर्शीय रूप में बड़े परंतु स्थूलदर्शीय रूप में छोटे क्षेत्र अवयव ΔS पर सूक्ष्मदर्शीय आवेश घनत्व है। σ का मात्रक C/m2 है।

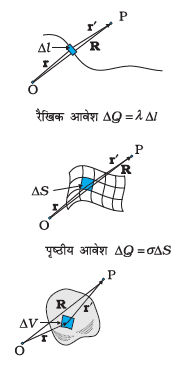
MP 12th Physics Continuous Charge Distribution

इसी प्रकार के दृष्टिकोण रैखिक आवेश वितरणों तथा आयतनी आवेश वितरणों पर भी लागू होते हैं। किसी तार का रैखिक आवेश घनत्व λ की परिभाषा

    \[\lambda = \frac{\Delta Q}{\Delta l} \qquad (1.24)\]

द्वारा की जाती है। यहाँ Δl सूक्ष्म स्तर पर तार का रैखिक अवयव है। तथापि सूक्ष्म आवेशित अवयवों की एक विशाल संख्या इसमें सम्मिलित है तथा ΔQ इस रैखिक अवयव में समाए आवेश है। λ का मात्रक C/m है। इसी प्रकार से आयतनी आवेश घनत्व (सरल शब्दों में जिसे आवेश घनत्व भी कहा जाता है) की परिभाषा भी

    \[\rho = \frac{\Delta Q}{\Delta V} \qquad (1.25)\]

द्वारा की जाती है। यहाँ ΔQ स्थूल रूप में छोटे आयतन अवयव ΔV में समाए वे आवेश हैं जो सूक्ष्म आवेशित अवयवों की विशाल संख्या को सम्मिलित करते हैं। ρ का मात्रक C/m3 है।

यहाँ संतत आवेश वितरण की हमारी धारणा यांत्रिकी में हमारे द्वारा अपनाई गई संतत संहति वितरण की धारणा के ही समान है। जब हम किसी द्रव के घनत्व का उल्लेख करते हैं तो उस समय वास्तव में हम उसके स्थूल घनत्व का ही उल्लेख कर रहे होते हैं। हम द्रव को एक संतत तरल मान लेते हैं तथा उसकी विविक्त आण्विक रचना की उपेक्षा कर देते हैं।

विविक्त आवेशों के निकाय के कारण विद्युत क्षेत्र प्राप्त करने [समीकरण (1.10)] की ही भाँति लगभग इसी ढंग से संतत आवेश वितरण के कारण विद्युत क्षेत्र प्राप्त किया जा सकता है। मान लीजिए किसी दिक्स्थान में संतत आवेश वितरण का आवेश घनत्व ρ है। कोई सुविधाजनक मूल बिंदु O चुनिए तथा मान लीजिए आवेश वितरण में किसी बिंदु का स्थिति सदिश r है। आवेश घनत्व ρ एक बिंदु से दूसरे बिंदु पर भिन्न हो सकता है, अर्थात यह r का फलन है। आवेश वितरण को ΔV आमाप के छोटे आयतन अवयवों में विभाजित कीजिए। आयतन अवयव ΔV में आवेश का परिमाण ρΔV है।

अब स्थिति सदिश R के साथ किसी भी व्यापक बिंदु P (आवेश वितरण के भीतर अथवा बाहर) पर विचार कीजिए। कूलॉम नियम द्वारा आवेश ρΔV के कारण विद्युत क्षेत्र

    \[\Delta \mathbf{E} = \frac{1}{4 \pi \epsilon_0} \frac{\rho \Delta V}{r'^2} \hat{\mathbf{r}}' \qquad (1.26)\]

यहाँ r′ आवेश अवयव तथा P के बीच की दूरी है, तथा r^′ आवेश अवयव से P की दिशा में एक एकांक सदिश है। अध्यारोपण सिद्धांत द्वारा संतत आवेश वितरण के कारण कुल विद्युत क्षेत्र विभिन्न आयतन-अवयवों के कारण विद्युत क्षेत्रों का योग करने पर प्राप्त होता है:

    \[\mathbf{E} = \frac{1}{4 \pi \epsilon_0} \sum_{\text{all } \Delta V} \frac{\rho \Delta V}{r'^2} \hat{\mathbf{r}}' \qquad (1.27)\]

ध्यान दीजिए ρ,r,r′ सभी के मान एक बिंदु से दूसरे बिंदु पर परिवर्तित हो सकते हैं। यथार्थ गणितीय विधि में हमें ΔV→0 लेना चाहिए और फिर यह योग एक समाकल बन जाता है। परंतु सरलता की दृष्टि से इस चर्चा को हम यहीं छोड़ रहे हैं। संक्षेप में कूलॉम नियम तथा अध्यारोपण सिद्धांत के उपयोग द्वारा किसी भी आवेश वितरण के लिए चाहे वह विविक्त हो अथवा संतत, अथवा अंशत: विविक्त और अंशत: संतत हो, विद्युत क्षेत्र ज्ञात किया जा सकता है।

संतत आवेश वितरण पर अक्सर पूछे जाने वाले प्रश्न (FAQs)

1. संतत आवेश वितरण क्या है?

संतत आवेश वितरण (Continuous Charge Distribution) का अर्थ है कि आवेश एक स्थान पर एक समान रूप से या लगातार (continuous) वितरित होता है, न कि अलग-अलग बिंदुओं पर। जब आवेशित कण (जैसे इलेक्ट्रॉन) बहुत पास-पास होते हैं और उनके बीच की दूरी को नगण्य माना जा सकता है, तब हम इस अवधारणा का उपयोग करते हैं। यह गणनाओं को सरल बनाने में मदद करता है।

2. संतत आवेश वितरण कितने प्रकार के होते हैं?

संतत आवेश वितरण तीन प्रकार के होते हैं:

  • रैखिक आवेश वितरण (Linear Charge Distribution): जब आवेश एक रेखा या तार पर वितरित होता है। इसे रैखिक आवेश घनत्व (λ) से दर्शाया जाता है। इसका मात्रक C/m (कुलॉम प्रति मीटर) होता है।
  • पृष्ठीय आवेश वितरण (Surface Charge Distribution): जब आवेश एक सतह या चादर पर वितरित होता है। इसे पृष्ठीय आवेश घनत्व (σ) से दर्शाया जाता है। इसका मात्रक C/m² (कुलॉम प्रति वर्ग मीटर) होता है।
  • आयतनी आवेश वितरण (Volume Charge Distribution): जब आवेश एक आयतन या त्रि-आयामी (three-dimensional) पिंड में वितरित होता है। इसे आयतनी आवेश घनत्व (ρ) से दर्शाया जाता है। इसका मात्रक C/m³ (कुलॉम प्रति घन मीटर) होता है।

3. आवेश घनत्व क्या है?

आवेश घनत्व (Charge Density) किसी भी प्रकार के आवेश वितरण में प्रति इकाई (per unit) लंबाई, क्षेत्रफल या आयतन में मौजूद आवेश की मात्रा होती है। यह आवेश वितरण की सघनता को मापता है।

4. संतत आवेश वितरण का अध्ययन क्यों महत्वपूर्ण है?

संतत आवेश वितरण का अध्ययन इसलिए महत्वपूर्ण है क्योंकि यह वास्तविक जीवन की स्थितियों को समझने में मदद करता है। उदाहरण के लिए, एक बड़ी आवेशित वस्तु (जैसे एक चालक का पृष्ठ) पर आवेश को अलग-अलग बिंदुओं में विभाजित करना व्यावहारिक नहीं है। ऐसे मामलों में, हम संतत आवेश वितरण की अवधारणा का उपयोग करके विद्युत क्षेत्र और बल की गणना आसानी से कर सकते हैं। यह इलेक्ट्रोस्टैटिक्स के कई प्रमुख सिद्धांतों, जैसे कि गॉस के नियम, का आधार भी बनता है।

5. संतत आवेश वितरण के कारण विद्युत क्षेत्र की गणना कैसे की जाती है?

संतत आवेश वितरण के कारण विद्युत क्षेत्र की गणना के लिए अध्यारोपण सिद्धांत (Principle of Superposition) और समाकलन (Integration) का उपयोग किया जाता है। आवेश वितरण को छोटे-छोटे अवयवों में विभाजित किया जाता है, प्रत्येक अवयव के कारण विद्युत क्षेत्र की गणना कूलॉम के नियम से की जाती है, और फिर इन सभी क्षेत्रों का योग (समाकलन) करके कुल विद्युत क्षेत्र ज्ञात किया जाता है।

    \[\mathbf{E} = \frac{1}{4\pi\epsilon_0} \int \frac{dq}{r^2} \hat{\mathbf{r}}\]

जहाँ dq आवेश का एक सूक्ष्म अवयव है और r उस अवयव से उस बिंदु तक की दूरी है जिस पर विद्युत क्षेत्र ज्ञात करना है।

Leave a Comment