MP Board 10th Surface area and volume Question Bank अध्याय 13: पृष्ठीय क्षेत्रफल और आयतन

MP Board 10th Surface area and volume Question Bank : अध्याय 13: पृष्ठीय क्षेत्रफल और आयतन

स्मरणीय बिंदु:

घनाभ का सम्पूर्ण पृष्ठ 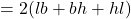$= 2(lb+bh+hl)$ होता है, जहाँ 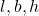$l, b, h$ क्रमशः घनाभ की लम्बाई, चौड़ाई और ऊँचाई हैं।
घनाभ का आयतन 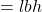$= lbh$ होता है, जहाँ 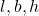$l, b, h$ क्रमशः घनाभ की लम्बाई, चौड़ाई और ऊँचाई हैं।
गोले का सम्पूर्ण पृष्ठ $= 4\pi r^2$ होता है, जहाँ $r$ गोले की त्रिज्या है।
गोले का आयतन 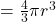$= \frac{4}{3}\pi r^3$ होता है, जहाँ $r$ गोले की त्रिज्या है।
अर्द्धगोले का वक्र पृष्ठ 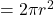$= 2\pi r^2$ होता है, जहाँ $r$ अर्द्धगोले की त्रिज्या है।
अर्द्धगोले का सम्पूर्ण पृष्ठ 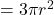$= 3\pi r^2$ होता है, जहाँ $r$ अर्द्धगोले की त्रिज्या है।
अर्द्धगोले का आयतन 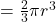$= \frac{2}{3}\pi r^3$ होता है, जहाँ $r$ अर्द्धगोले की त्रिज्या है।
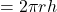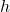बेलन का वक्र पृष्ठ $= 2\pi rh$ होता है, जहाँ $r$ एवं $h$ क्रमशः बेलन के आधार की त्रिज्या एवं बेलन की ऊँचाई हैं।
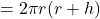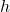बेलन का सम्पूर्ण पृष्ठ $= 2\pi r(r+h)$ होता है, जहाँ $r$ एवं $h$ क्रमशः बेलन के आधार की त्रिज्या एवं बेलन की ऊँचाई हैं।
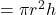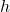बेलन का आयतन $= \pi r^2 h$ होता है, जहाँ $r$ एवं $h$ क्रमशः बेलन के आधार की त्रिज्या एवं बेलन की ऊँचाई हैं।
शंकु का वक्र पृष्ठ 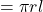$= \pi rl$ होता है, जहाँ $r$ एवं $l$ क्रमशः शंकु के आधार की त्रिज्या एवं शंकु की त्रियक ऊँचाई हैं।
शंकु का सम्पूर्ण पृष्ठ 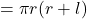$= \pi r(r+l)$ होता है, जहाँ $r$ एवं $l$ क्रमशः शंकु के आधार की त्रिज्या एवं शंकु की त्रियक ऊँचाई हैं।
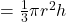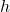शंकु का आयतन $= \frac{1}{3}\pi r^2 h$ होता है, जहाँ $r$ एवं $h$ क्रमशः शंकु के आधार की त्रिज्या एवं शंकु की ऊँचाई हैं।

MP Board 10th Surface area and volume Question Bank : अध्याय 13: पृष्ठीय क्षेत्रफल और आयतन

प्र.1. सही विकल्प चुनिये:

WhatsApp Channel Join Now

Telegram Channel Join Now

एक कीप (फनल) निम्नलिखित का उदाहरण है:
(a) एक शंकु और एक बेलन
(b) शंकु का छिन्नक और बेलन
(c) एक अर्द्धगोला और एक बेलन
(d) एक अर्द्धगोला और एक शंकु
यदि पानी से पूरा भरे हुए,, त्रिज्या 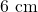$6 \text{ cm}$ और ऊँचाई 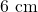$6 \text{ cm}$ वाले एक बेलनाकार कप में त्रिज्या 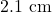$2.1 \text{ cm}$ का एक कंचा डाला जाये, तो बेलनाकार कप में से कितना पानी बाहर जायेगा:
(a)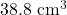 $38.8 \text{ cm}^3$
(b)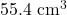 $55.4 \text{ c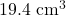m}^3$
(c) $19.4 \text{ cm}^3$
(d)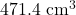 $471.4 \text{ cm}^3$

प्र.2. रिक्त स्थान की पूर्ति कीजिये:

एक किनारें पर बेलनाकार बनाई गई पेंसिल एक शंकु और एक ……. का संयोजन है।
यदि $r$ एवं $l$ क्रमशः शंकु के आधार की त्रिज्या एवं शंकु की त्रियक ऊँचाई हैं तो शंकु का वक्र पृष्ठ ……. होता है।

प्र. 03 सही जोड़ी बनाओ।

स्तम्भ-(1)	स्तम्भ-(2)
(i) एक कीप (फनल) संयोजन है :	(अ) एक गोले और और एक बेलन का
(ii) एक सुराही संयोजन है :	(ब) एक शंकु के छिन्नक और एक बेलन का
(iii) एक साहुल (भौरा) संयोजन है	(स) दो शंकु और एक बेलन
(iv) एक गिल्ली संयोजन है	(द) एक अर्द्ध-गोले और एक शंकु का

प्र.4. एक शब्द / वाक्य में उत्तर दीजिए:

गिल्ली डंडे के खेल में, गिल्ली का आकार किन-किन ठोसों का संयोजन है?
बैडमिंटन खेलने में प्रयुक्त की जाने वाली शटलकॉक (चिड़िया) किन-किन ठोसों का संयोजन है?
घनाभ के सम्पूर्ण पृष्ठ का सूत्र लिखिए।
घनाभ के आयतन का सूत्र लिखिए।
गोले के सम्पूर्ण पृष्ठ का सूत्र लिखिए।
गोले के आयतन का सूत्र लिखिए।
अर्द्धगोले के वक्रपृष्ठ का सूत्र लिखिए।
अर्द्धगोले के सम्पूर्ण पृष्ठ का सूत्र लिखिए।
अर्द्धगोले के आयतन का सूत्र लिखिए।
बेलन के वक्रपृष्ठ का सूत्र लिखिए।
बेलन के सम्पूर्ण पृष्ठ का सूत्र लिखिए।
बेलन के आयतन का सूत्र लिखिए।
शंकु के वक्रपृष्ठ का सूत्र लिखिए।
शंकु के सम्पूर्ण पृष्ठ का सूत्र लिखिए।
शंकु के आयतन का सूत्र लिखिए।

प्र. 5. सत्य / असत्य लिखिए:

एक किनारे पर बेलनाकार बनाई गई पेंसिल एक शंकु और एक बेलन का संयोजन है।
एक कीप (फनल) एक शंकु और एक बेलन का संयोजन है।
अर्द्धगोले का सम्पूर्ण पृष्ठ 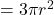$= 3\pi r^2$ होता है, जहाँ $r$ अर्द्धगोले की त्रिज्या है।
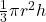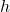शंकु का आयतन $\frac{1}{3}\pi r^2 h$ होता है, जहाँ $r$ आधार की त्रिज्या एवं $h$ शंकु की ऊँचाई है।

प्र.6. दो घनों, जिनमें से प्रत्येक का आयतन $64 \text{ cm}^3$ है, के संलग्न फलकों को मिलाकर एक ठोस बनाया जाता है। इससे प्राप्त घनाभ का पृष्ठीय क्षेत्रफल ज्ञात कीजिए।

प्र.7. एक खिलौना त्रिज्या $3.5 \text{ cm}$ वाले एक शंकु के आकार का है, जो उसी त्रिज्या वाले एक अर्द्धगोले पर अध्यारोपित है। इस खिलौने की सम्पूर्ण ऊँचाई $15.5 \text{cm}$ है। इस खिलौने का सम्पूर्ण पृष्ठीय क्षेत्रफल ज्ञात कीजिए।

प्र.8 कोई बर्तन एक खोखले अर्द्धगोले के आकार का है जिसके ऊपर एक खोखला बेलन अध्यारोपित है। अर्द्धगोले का व्यास $14 \text{ cm}$ है और इस बर्तन (पात्र) की कुल ऊँचाई $13 \text{ cm}$ है। इस बर्तन का आतंरिक पृष्ठीय क्षेत्रफल
ज्ञात कीजिए।

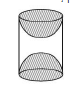
प्र.9. लकड़ी के एक ठोस बेलन के प्रत्येक सिरे पर एक अर्द्धगोला खोदकर निकालते हुए, एक वस्तु बनाई गई है, जैसा कि आकृति में दर्शाया गया है। यदि बेलन की ऊँचाई $10 \text{ cm}$ है और आधार की त्रिज्या $3.5 \text{ cm}$ है तो तो इस वस्तु का सम्पूर्ण पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
[आकृति]

प्र.10. एक ठोस एक अर्द्धगोले पर खड़े एक शंकु के आकार का है जिनकी त्रिज्याएँ $1 \text{ cm}$ हैं तथा शंकु की ऊँचाई उसकी त्रिज्या के बराबर है। इस ठोस का आयतन $\pi$ के पदों में ज्ञात कीजिए।

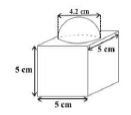
प्र.11. आकृति में दर्शाया गया सजावट के लिए प्रयोग होने वाला ब्लॉक दो ठोसों से मिलकर बना है। इनमें से एक घन है और दूसरा अर्द्धगोला है। इस ब्लॉक का आधार $5 \text{ cm}$ कोर या किनारे वाला एक घन है और उसके ऊपर लगे हुए अर्द्धगोले का व्यास $4.2 \text{ cm}$ है। इस ब्लॉक का सम्पूर्ण पृष्ठीय क्षेत्रफल ज्ञात कीजिए। ( $\pi = \frac{22}{7}$ लीजिए)
[आकृति]

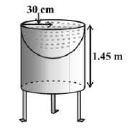
प्र.12. मयंक ने अपने बगीचे के लिए एक पक्षी स्नानागार बनाया जिसका आकार एक खोखले बेलन जैसा है जिसके एक सिरे पर अर्द्धगोलाकार बर्तन बना हुआ है (देखिए आकृति)। बेलन की ऊँचाई $1.45 \text{ m}$ है और उसकी त्रिज्या $30 \text{ cm}$ है। इस पक्षी स्नानागार का सम्पूर्ण पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
[आकृति]

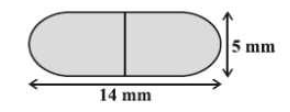
प्र.13. दवा का एक कैप्सूल एक बेलन के आकार का है जिसके दोनों सिरों पर एक -एक अर्द्धगोला लगा हुआ है (देखिए आकृति)। पूरे कैप्सूल की लम्बाई $14 \text{ mm}$ है और उसका व्यास $5 \text{ mm}$ है। इसका पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
[आकृति]

प्र.14. भुजा $7 \text{ cm}$ वाले एक घनाकार ब्लॉक के ऊपर एक अर्द्धगोला रखा हुआ है। अर्द्धगोले का अधिकतम व्यास क्या हो सकता है? इस प्रकार बने ठोस का पृष्ठीय क्षेत्रफल ज्ञात कीजिए।

प्र.15. एक घनाकार ब्लॉक के एक फलक को अन्दर की ओर से काट कर एक अर्द्धगोलाकार गड्ढा इस प्रकार बनाया गया है कि अर्द्धगोले का व्यास घन के एक किनारे के बराबर है। शेष बचे ठोस का पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
प्र.16. ऊँचाई $2.4 \text{ cm}$ और व्यास $1.4 \text{ cm}$ वाले एक ठोस बेलन में से इसी ऊँचाई और इसी व्यास वाला एक शंक्वाकार खोल काट लिया जाता है। शेष बचे ठोस का निकटतम वर्ग सेंटीमीटर तक पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
प्र.17. एक गुलाबजामुन में उसके आयतन की लगभग

*** QuickLaTeX cannot compile formula:
30 \text{ %}

*** Error message:
File ended while scanning use of \text@.
Emergency stop.

चीनी की चाशनी होती, यदि प्रत्येक गुलाबजामुन एक बेलन के आकार का है, जिसके दोनों सिरे अर्द्धगोलाकार हैं तथा इसकी लम्बाई $5 \text{ cm}$ और व्यास $2.8 \text{ cm}$ है। (देखिए आकृति )
[आकृति]

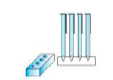
प्र.18. एक कलमदान घनाभ के आकार की एक लकड़ी से बना है जिसमें कलम रखने के लिए चार शंक्वाकार गड्ढे बने हुए हैं। घनाभ की विमाएँ $15 \text{ cm X } 10 \text{ cm X } 3.5 \text{ cm}$ हैं। प्रत्येक गड्ढे की त्रिज्या $0.5 \text{ cm}$ है और गहराई $1.4 \text{ cm}$ है। पूरे कलमदान में लकड़ी का आयतन ज्ञात कीजिए।
[आकृति]

प्र.19. ऊँचाई $220 \text{ cm}$ और आधार व्यास $24 \text{ cm}$ वाले एक बेलन, जिस पर ऊँचाई $60 \text{ cm}$ और त्रिज्या $8 \text{ cm}$ वाला एक अन्य बेलन आरोपित है, से लोहे का एक स्तम्भ बना है। इस स्तम्भ का द्रव्यमान ज्ञात कीजिए, जबकि दिया है $1 \text{ cm}^3$ लोहे का द्रव्यमान लगभग $8 \text{ g}$ होता है। ( $\pi = 3.14$ लीजिए)

उत्तरमाला
(वस्तुनिष्ठ प्रश्न)

उ.1. 1. (b) शंकु का छिन्नक और बेलन

(a) $38.8 \text{ cm}^3$

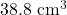
उ.2. 1. बेलन 2. $\pi rl$

उ.3. (i). $\leftrightarrow$ (ब), (ii). $\leftrightarrow$ (अ), (iii). $\leftrightarrow$ (द), (iv). $\leftrightarrow$ (स)

उ.4.

दो शंकु और एक बेलन का
एक शंकु के छिन्नक और एक अर्द्ध-गोले का
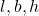घनाभ का सम्पूर्ण पृष्ठ $= 2[lb+bh+hl]$ होता है, जहाँ $l, b, h$ क्रमशः घनाभ की लम्बाई , चौड़ाई और ऊँचाई हैं।
घनाभ का आयतन 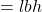$= lbh$ होता है, जहाँ 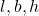$l, b, h$ क्रमशः घनाभ की लम्बाई, चौड़ाई और ऊँचाई हैं।
गोले का सम्पूर्ण पृष्ठ $= 4\pi r^2$ होता है, जहाँ $r$ गोले की त्रिज्या है।
गोले का आयतन 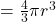$= \frac{4}{3}\pi r^3$ होता है, जहाँ $r$ गोले की त्रिज्या है।
अर्द्धगोले का वक्र पृष्ठ 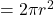$= 2\pi r^2$ होता है, जहाँ $r$ अर्द्धगोले की त्रिज्या है।
अर्द्धगोले का सम्पूर्ण पृष्ठ 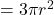$= 3\pi r^2$ होता है, जहाँ $r$ अर्द्धगोले की त्रिज्या है।
अर्द्धगोले का आयतन 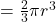$= \frac{2}{3}\pi r^3$ होता है, जहाँ $r$ अर्द्धगोले की त्रिज्या है।
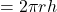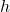बेलन का वक्र पृष्ठ $= 2\pi rh$ होता है, जहाँ $r$ एवं $h$ क्रमशः बेलन के आधार की त्रिज्या एवं बेलन की ऊँचाई हैं।
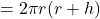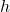बेलन का सम्पूर्ण पृष्ठ $= 2\pi r(r+h)$ होता है, जहाँ $r$ एवं $h$ क्रमशः बेलन के आधार की त्रिज्या एवं बेलन की ऊँचाई हैं।
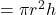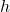बेलन का आयतन $= \pi r^2 h$ होता है, जहाँ $r$ एवं $h$ क्रमशः बेलन के आधार की त्रिज्या एवं बेलन की ऊँचाई हैं।
शंकु का वक्र पृष्ठ 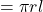$= \pi rl$ होता है, जहाँ $r$ एवं $l$ क्रमशः शंकु के आधार की त्रिज्या एवं शंकु की त्रियक ऊँचाई हैं।
शंकु का सम्पूर्ण पृष्ठ 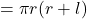$= \pi r(r+l)$ होता है, जहाँ $r$ एवं $l$ क्रमशः शंकु के आधार की त्रिज्या एवं शंकु की त्रियक ऊँचाई हैं।
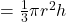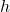शंकु का आयतन $= \frac{1}{3}\pi r^2 h$ होता है, जहाँ $r$ एवं $h$ क्रमशः शंकु के आधार की त्रिज्या एवं शंकु की ऊँचाई हैं।

उ.5. 1. सत्य

असत्य
सत्य
सत्य

MP Board 10th Surface area and volume Question Bank : अध्याय 13: पृष्ठीय क्षेत्रफल और आयतन

Leave a Comment Cancel reply