अध्याय 2: बहुपद MP Board 10th mathematics Polynomials Question Bank
स्मरणीय बिंदु :
- यदि
 एक चर है,
एक चर है,  एक प्राकृत संख्या है और
एक प्राकृत संख्या है और 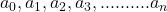 वास्तविक संख्याएँ हैं तो
वास्तविक संख्याएँ हैं तो 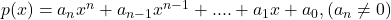 चर
चर  में एक बहुपद कहलाता है |
में एक बहुपद कहलाता है | - बहुपद
 में
में  की उच्चतम घात, बहुपद की घात (degree) कहलाती है | उदाहरण के लिए
की उच्चतम घात, बहुपद की घात (degree) कहलाती है | उदाहरण के लिए 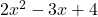 चर
चर  में घात 2 का बहुपद है |
में घात 2 का बहुपद है | - घात 1 के बहुपद को रैखिक बहुपद (linear polynomial) कहते हैं |
- घात 2 के बहुपद को द्विघात बहुपद (quadratic polynomial) कहते हैं |
- घात 3 के बहुपद को त्रिघात बहुपद (cubic polynomial) कहते हैं |
- यदि
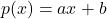 का शून्यक
का शून्यक  है, तो
है, तो  से हमें
से हमें 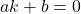 अर्थात्
अर्थात् 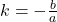 प्राप्त होता है |
प्राप्त होता है | - एक वास्तविक संख्या
 बहुपद
बहुपद  का शून्यक है, यदि
का शून्यक है, यदि  है |
है | - रैखिक बहुपद
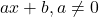 का केवल एक शून्यक है, जो उस बिंदु का
का केवल एक शून्यक है, जो उस बिंदु का  -निर्देशांक है, जहाँ
-निर्देशांक है, जहाँ  का ग्राफ
का ग्राफ  -अक्ष को प्रतिच्छेद करता है |
-अक्ष को प्रतिच्छेद करता है | 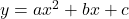 के ग्राफ के आकार का प्रेक्षण करने से तीन निम्नलिखित स्थितियाँ संभावित हैं :स्थिति (i)यहाँ ग्राफ
के ग्राफ के आकार का प्रेक्षण करने से तीन निम्नलिखित स्थितियाँ संभावित हैं :स्थिति (i)यहाँ ग्राफ  -अक्ष को दो भिन्न बिन्दुओं A और A’ पर काटता है | इस स्थिति में, A और A’ के
-अक्ष को दो भिन्न बिन्दुओं A और A’ पर काटता है | इस स्थिति में, A और A’ के  -निर्देशांक द्विघात बहुपद
-निर्देशांक द्विघात बहुपद 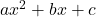 के दो शून्यक हैं |
के दो शून्यक हैं |- घात
 के दिए गए बहुपद
के दिए गए बहुपद  के लिए,
के लिए,  का ग्राफ
का ग्राफ  -अक्ष को अधिक से अधिक
-अक्ष को अधिक से अधिक  बिन्दुओं पर प्रतिच्छेद करता है | अतः घात
बिन्दुओं पर प्रतिच्छेद करता है | अतः घात  के किसी बहुपद के अधिक से अधिक
के किसी बहुपद के अधिक से अधिक  शून्यक हो सकते हैं |
शून्यक हो सकते हैं | - बहुपद के अधिकतम उतने शून्यक हो सकते हैं, जितनी बहुपद की घात है |
- यदि
 रैखिक बहुपद
रैखिक बहुपद 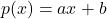 का शून्यक है, तो
का शून्यक है, तो 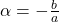 होगा |
होगा | - यदि
 और
और  द्विघात बहुपद
द्विघात बहुपद 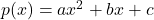 के शून्यक हैं, तो
के शून्यक हैं, तो  और
और  ,
,  के गुणनखंड होंगे |
के गुणनखंड होंगे | - एक द्विघात बहुपद
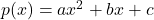 के अधिक से अधिक दो शून्यक हो सकते हैं |
के अधिक से अधिक दो शून्यक हो सकते हैं | - एक द्विघात बहुपद
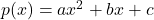 के शून्यक
के शून्यक  और
और  हों तो
हों तो और
और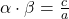
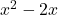 के शून्यक 0 और 2 हैं |
के शून्यक 0 और 2 हैं | के शून्यक
के शून्यक  हैं |
हैं |- दो बहुपदों का योग भी एक बहुपद होता है |
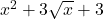 बहुपद नहीं है |
बहुपद नहीं है |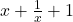 बहुपद नहीं है |
बहुपद नहीं है |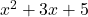 एक घात 2 का बहुपद है |
एक घात 2 का बहुपद है |
प्र.1. सही विकल्प चुनिये:
1. यदि द्विघात बहुपद ![]() के शून्यक
के शून्यक ![]() और
और ![]() हों, तो
हों, तो ![]() का मान होगा:
का मान होगा:
(a) ![]()
(b) ![]()
(c) ![]()
(d) ![]()
उत्तर: (a) ![]()
2. यदि द्विघात बहुपद ![]() के शून्यक
के शून्यक ![]() और
और ![]() हों, तो
हों, तो ![]() का मान होगा:
का मान होगा:
(a) ![]()
(b) ![]()
(c) ![]()
(d) ![]()
उत्तर: (c) ![]()
3. रैखिक बहुपद ![]() का शून्यक होगा:
का शून्यक होगा:
(a) ![]()
(b) ![]()
(c) ![]()
(d) ![]()
उत्तर: (c) ![]()
4. बहुपद ![]() के शून्यक होंगे:
के शून्यक होंगे:
(a) ![]()
(b) ![]()
(c) ![]()
(d) ![]()
उत्तर: (a) ![]()
5. बहुपद ![]() के शून्यक होंगे:
के शून्यक होंगे:
(a) ![]()
(b) ![]()
(c) ![]()
(d) ![]()
उत्तर: (b) ![]()
6. बहुपद ![]() के लिए घात होगी:
के लिए घात होगी:
(a) ![]()
(b) ![]()
(c) ![]()
(d) ![]()
उत्तर: (d) 5
7. यदि द्विघात बहुपद के शून्यक ![]() तथा
तथा ![]() हों तो द्विघात बहुपद होगा:
हों तो द्विघात बहुपद होगा:
(a) ![]()
(b) ![]()
(c) ![]()
(d) ![]()
उत्तर: (a) ![]()
8. किसी बहुपद के कुल शून्यक, उस बहुपद के आरेख के निम्नलिखित पर प्रतिच्छेदन के कुल बिन्दुओं की संख्या के बराबर होते हैं:
(a) ![]() -अक्ष पर
-अक्ष पर
(b) ![]() -अक्ष पर
-अक्ष पर
(c) ![]() -अक्ष तथा
-अक्ष तथा ![]() -अक्ष दोनों पर
-अक्ष दोनों पर
(d) इनमें से कोई नहीं
उत्तर: (a) ![]() -अक्ष पर
-अक्ष पर
9. बहुपद ![]() की घात होगी:
की घात होगी:
(a) ![]()
(b) ![]()
(c) ![]()
(d) ![]()
उत्तर: (c) 2
10. बहुपद ![]() के शून्यकों का गुणनफल होगा:
के शून्यकों का गुणनफल होगा:
(a) ![]()
(b) ![]()
(c) ![]()
(d) ![]()
उत्तर: (c) 24
11. बहुपद ![]() के शून्यकों का योग होगा:
के शून्यकों का योग होगा:
(a) ![]()
(b) ![]()
(c) ![]()
(d) ![]()
उत्तर: (a) 4
12. निम्नलिखित में से कौनसा बहुपद नहीं है:
(a) ![]()
(b) ![]()
(c) ![]()
(d) ![]()
उत्तर: (c) ![]()
- प्र.2. रिक्त स्थान की पूर्ति कीजिये:
- रैखिक बहुपद
 का शून्यक
का शून्यक 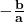 है।
है। - दो बहुपदों का गुणनफल एक
 होता है।
होता है। - बहुपद
 के शून्यकों का योग
के शून्यकों का योग 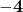 है। (
है। ( 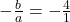 )
) - बहुपद
 के शून्यकों का गुणनफल
के शून्यकों का गुणनफल 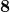 है। (
है। ( 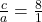 )
) - यदि बहुपद
 का एक शून्यक
का एक शून्यक  हो, तब
हो, तब  का मान
का मान 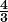 होगा।
होगा।
- (हल:
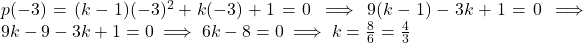 )
)
- (हल:
- घात एक वाले बहुपद
 बहुपद कहलाते हैं।
बहुपद कहलाते हैं। - द्विघात बहुपद में शून्यकों की अधिकतम संख्या
 होती है।
होती है। - बहुपद
 की घात
की घात 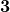 है।
है। - यदि
 और
और  बहुपद
बहुपद  के शून्यक हैं तो
के शून्यक हैं तो  का मान
का मान 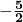 होगा। (
होगा। ( 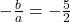 )
)
प्र.3. सत्य / असत्य लिखिये:
- व्यंजक
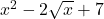 बहुपद नहीं है।उत्तर: सत्य (क्योंकि
बहुपद नहीं है।उत्तर: सत्य (क्योंकि  की घात
की घात 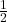 है, जो प्राकृत संख्या नहीं है।)
है, जो प्राकृत संख्या नहीं है।) - शून्य बहुपद की घात शून्य है।उत्तर: असत्य (शून्य बहुपद की घात अपरिभाषित होती है।)
- शून्य बहुपद की घात अपरिभाषित है।उत्तर: सत्य
 घात वाले बहुपद के अधिकतम
घात वाले बहुपद के अधिकतम  शून्यक हो सकते हैं।उत्तर: सत्य
शून्यक हो सकते हैं।उत्तर: सत्य- द्विघात बहुपद के अधिक से अधिक दो शून्यक हो सकते हैं।उत्तर: सत्य
- यदि
 और
और  बहुपद
बहुपद 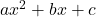 के शून्यक हैं तो
के शून्यक हैं तो  होता है।उत्तर: सत्य
होता है।उत्तर: सत्य - त्रिघात बहुपद की अधिकतम घात दो होती है।उत्तर: असत्य (त्रिघात बहुपद की घात 3 होती है।)
प्र.4. सही जोड़ी मिलाइए:
| स्तम्भ – अ | स्तम्भ – ब | उत्तर |
| 1. द्विघात बहुपद | (i). | 1. |
| 2. बहुपद | (ii). | 2. |
| 3. त्रिघात बहुपद है : | (iii). | 3. |
| 4. रैखिक बहुपद है : | (iv). | 4. |
| 5. द्विघात बहुपद | (v). | 5. |
प्र.5. एक शब्द / वाक्य में उत्तर दीजिये:
- रैखिक बहुपद की घात कितनी होती है?उत्तर: 1
- द्विघात बहुपद की घात कितनी होती है?उत्तर: 2
- त्रिघात बहुपद की घात कितनी होती है?उत्तर: 3
प्र.6 से प्र.26 तक के हल:
प्र.6. बहुपद ![]() के शून्यक ज्ञात कीजिए और शून्यकों तथा गुणांकों के बीच के संबंध की सत्यता की जाँच कीजिए।
के शून्यक ज्ञात कीजिए और शून्यकों तथा गुणांकों के बीच के संबंध की सत्यता की जाँच कीजिए।
- शून्यक:
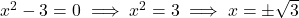 शून्यक
शून्यक 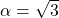 और
और 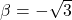 हैं।
हैं। - जाँच:यहाँ
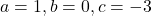
- शून्यकों का योग
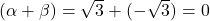 सूत्र से:
सूत्र से: 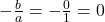
- शून्यकों का गुणनफल
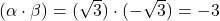 सूत्र से:
सूत्र से: 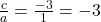 (सत्यता की जाँच हुई)
(सत्यता की जाँच हुई)
- शून्यकों का योग
प्र.7. द्विघात बहुपद ![]() के शून्यक ज्ञात कीजिए और शून्यकों तथा गुणांकों के बीच के संबंध की सत्यता की जाँच कीजिए।
के शून्यक ज्ञात कीजिए और शून्यकों तथा गुणांकों के बीच के संबंध की सत्यता की जाँच कीजिए।
शून्यक:![]()
![]()
शून्यक ![]() और
और ![]() हैं।
हैं।
जाँच:
यहाँ ![]()
शून्यकों का योग ![]()
सूत्र से: ![]()
शून्यकों का गुणनफल ![]()
सूत्र से: ![]()
(सत्यता की जाँच हुई)
प्र.8. यदि बहुपद के शून्यकों का योग 0 एवं गुणनफल भी ![]() है तो बहुपद ज्ञात कीजिए।
है तो बहुपद ज्ञात कीजिए।
हल: बहुपद का सूत्र: ![]()
![]()
(नोट: प्रश्न में “गुणनफल भी ![]() ” लिखा है, यदि यह “गुणनफल
” लिखा है, यदि यह “गुणनफल ![]() ” है, तो उत्तर
” है, तो उत्तर ![]() है।)
है।)
- प्र.9. बहुपद
 के शून्यक ज्ञात कीजिए और शून्यकों तथा गुणांकों के बीच के संबंध की सत्यता की जाँच कीजिए।
के शून्यक ज्ञात कीजिए और शून्यकों तथा गुणांकों के बीच के संबंध की सत्यता की जाँच कीजिए।
शून्यक:![]()
शून्यक ![]() और
और ![]() हैं।
हैं।
जाँच:
यहाँ ![]()
शून्यकों का योग ![]()
सूत्र से: ![]()
शून्यकों का गुणनफल ![]()
सूत्र से: ![]()
(सत्यता की जाँच हुई)
प्र.10. बहुपद ![]() के शून्यक ज्ञात कीजिए और शून्यकों तथा गुणांकों के बीच के संबंध की सत्यता की जाँच कीजिए।
के शून्यक ज्ञात कीजिए और शून्यकों तथा गुणांकों के बीच के संबंध की सत्यता की जाँच कीजिए।
शून्यक: (पहले सही क्रम में लिखें: ![]() )
)![]()
![]()
शून्यक ![]() और
और ![]() हैं।
हैं।
जाँच:
यहाँ ![]()
शून्यकों का योग ![]()
सूत्र से: ![]()
शून्यकों का गुणनफल ![]()
सूत्र से: ![]()
(सत्यता की जाँच हुई)
प्र.11. एक द्विघात बहुपद ज्ञात कीजिए, जिसके शून्यकों के योग तथा गुणनफल क्रमशः ![]() हैं।
हैं।
हल: सूत्र: ![]()
![]()
(या, 4 से गुणा करने पर: ![]() )
)
प्र.12. एक द्विघात बहुपद ज्ञात कीजिए, जिसके शून्यकों के योग तथा गुणनफल क्रमशः ![]() हैं।
हैं।
हल: सूत्र: ![]()
![]()
(या, 3 से गुणा करने पर: ![]() )
)
प्र.13. एक द्विघात बहुपद ज्ञात कीजिए, जिसके शून्यकों के योग तथा गुणनफल क्रमशः 1 और 1 हैं।
हल: सूत्र: ![]()
![]()
प्र.14. एक द्विघात बहुपद ज्ञात कीजिए, जिसके शून्यकों के योग तथा गुणनफल क्रमशः ![]() और
और ![]() हैं।
हैं।
हल: सूत्र: ![]()
![]()
प्र.15. एक द्विघात बहुपद ज्ञात कीजिए, जिसके शून्यकों के योग तथा गुणनफल क्रमशः ![]() और
और ![]() हैं।
हैं।
हल: सूत्र: ![]()
![]()
(या, 4 से गुणा करने पर: ![]() )
)
प्र.16. एक द्विघात बहुपद ज्ञात कीजिए, जिसके शून्यकों के योग तथा गुणनफल क्रमशः 4 और 1 हैं।
हल: सूत्र: ![]()
![]()
प्र.17. त्रिघात बहुपद ![]() के शून्यक
के शून्यक ![]() एवं
एवं ![]() हैं,
हैं, ![]() का मान ज्ञात कीजिए।
का मान ज्ञात कीजिए।
हल: त्रिघात बहुपद के लिए, शून्यकों का योग ![]()
यहाँ ![]()
![]()
प्र.18. ![]() के शून्यक
के शून्यक ![]() एवं
एवं ![]() हैं तो
हैं तो ![]() के मान ज्ञात कीजिये।
के मान ज्ञात कीजिये।
हल: शून्यकों का योग ![]()
यहाँ ![]()
![]()
प्र.19. ![]() के शून्यक ज्ञात कीजिये।
के शून्यक ज्ञात कीजिये।
हल: ![]()
![]()
![]()
शून्यक 0 और ![]() हैं।
हैं।
प्र.20. यदि बहुपद ![]() के शून्यक
के शून्यक ![]() हैं तो
हैं तो ![]() का मान ज्ञात कीजिये।
का मान ज्ञात कीजिये।
हल:
हमें ज्ञात करना है: ![]()
बहुपद ![]() से:
से: ![]()
शून्यकों का योग ![]()
शून्यकों का गुणनफल ![]()
मान रखने पर: ![]()
प्र.21. द्विघात बहुपद ![]() के शून्यक ज्ञात कीजिए और शून्यकों तथा गुणांकों के बीच के संबंध की सत्यता की जाँच कीजिए।
के शून्यक ज्ञात कीजिए और शून्यकों तथा गुणांकों के बीच के संबंध की सत्यता की जाँच कीजिए।
शून्यक:![]()
![]()
शून्यक ![]() और
और ![]() हैं।
हैं।
जाँच:
यहाँ ![]()
शून्यकों का योग ![]()
सूत्र से: ![]()
शून्यकों का गुणनफल ![]()
सूत्र से: ![]()
(सत्यता की जाँच हुई)
प्र.22. द्विघात बहुपद ![]() के शून्यक ज्ञात कीजिए और शून्यकों तथा गुणांकों के बीच के संबंध की सत्यता की जाँच कीजिए।
के शून्यक ज्ञात कीजिए और शून्यकों तथा गुणांकों के बीच के संबंध की सत्यता की जाँच कीजिए।
शून्यक:![]()
![]()
शून्यक ![]() और
और ![]() हैं।
हैं।
जाँच:
यहाँ ![]()
शून्यकों का योग ![]()
सूत्र से: ![]()
शून्यकों का गुणनफल ![]()
सूत्र से: ![]()
(सत्यता की जाँच हुई)
प्र.23. द्विघात बहुपद ![]() के शून्यक ज्ञात कीजिए और शून्यकों तथा गुणांकों के बीच के संबंध की सत्यता की जाँच कीजिए।
के शून्यक ज्ञात कीजिए और शून्यकों तथा गुणांकों के बीच के संबंध की सत्यता की जाँच कीजिए।
(यह प्रश्न प्र.7 के समान है।)
शून्यक: ![]() और
और ![]()
जाँच: योग = ![]() (सूत्र
(सूत्र ![]() ), गुणनफल = 10 (सूत्र
), गुणनफल = 10 (सूत्र ![]() )
)
प्र.24. द्विघात बहुपद ![]() के शून्यक ज्ञात कीजिए और शून्यकों तथा गुणांकों के बीच के संबंध की सत्यता की जाँच कीजिए।
के शून्यक ज्ञात कीजिए और शून्यकों तथा गुणांकों के बीच के संबंध की सत्यता की जाँच कीजिए।
शून्यक:![]()
![]()
शून्यक ![]() और
और ![]() हैं।
हैं।
जाँच:
यहाँ ![]()
शून्यकों का योग ![]()
सूत्र से: ![]()
शून्यकों का गुणनफल ![]()
सूत्र से: ![]()
(सत्यता की जाँच हुई)
प्र.25. द्विघात बहुपद ![]() के शून्यक ज्ञात कीजिए और शून्यकों तथा गुणांकों के बीच के संबंध की सत्यता की जाँच कीजिए।
के शून्यक ज्ञात कीजिए और शून्यकों तथा गुणांकों के बीच के संबंध की सत्यता की जाँच कीजिए।
शून्यक:![]()
![]()
शून्यक ![]() और
और ![]() हैं।
हैं।
जाँच:
यहाँ ![]()
शून्यकों का योग ![]()
सूत्र से: ![]()
शून्यकों का गुणनफल ![]()
सूत्र से: ![]()
(सत्यता की जाँच हुई)
प्र.26. यदि बहुपद ![]() के शून्यक
के शून्यक ![]() हों तो
हों तो ![]() और
और ![]() का मान ज्ञात कीजिये।
का मान ज्ञात कीजिये।
हल:
बहुपद ![]() के लिए:
के लिए:![]()
शून्यकों का योग ![]()
![]()
![]()
अब, शून्यकों का गुणनफल ![]()
![]()
![]()
![]() का मान रखने पर:
का मान रखने पर:![]()
![]()
![]()
उत्तर: ![]() और
और ![]()