MP Board 10th mathematics Real numbers Question Bank: आपने जो विषय (HCF और LCM) चुना है, उससे जुड़े कुछ महत्वपूर्ण तथ्य यहाँ दिए गए हैं जो परीक्षा के लिए उपयोगी हैं:
- अभाज्य गुणनखंडन (Prime Factorization): किसी भी भाज्य संख्या को उसके अभाज्य गुणनखंडों के गुणनफल के रूप में लिखना, HCF और LCM निकालने का पहला और सबसे महत्वपूर्ण कदम है।
- उदाहरण:
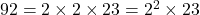 .
.
- उदाहरण:
- HCF (महत्तम समापवर्तक): दो या अधिक संख्याओं का HCF, उन संख्याओं में मौजूद “उभयनिष्ठ (common) अभाज्य गुणनखंडों की सबसे छोटी घातों” का गुणनफल होता है।
- आपके उदाहरण (510 और 92) में: एकमात्र उभयनिष्ठ गुणनखंड ‘2’ है, और उसकी सबसे छोटी घात
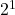 है। इसलिए HCF = 2 है।
है। इसलिए HCF = 2 है।
- आपके उदाहरण (510 और 92) में: एकमात्र उभयनिष्ठ गुणनखंड ‘2’ है, और उसकी सबसे छोटी घात
- LCM (लघुत्तम समापवर्त्य): दो या अधिक संख्याओं का LCM, उन संख्याओं के “सभी अभाज्य गुणनखंडों की सबसे बड़ी घातों” का गुणनफल होता है।
- आपके उदाहरण में: सभी गुणनखंड 2, 3, 5, 17, 23 हैं। इनकी सबसे बड़ी घातें
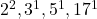 और
और 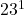 हैं, जिनका गुणनफल 23460 है।
हैं, जिनका गुणनफल 23460 है।
- आपके उदाहरण में: सभी गुणनखंड 2, 3, 5, 17, 23 हैं। इनकी सबसे बड़ी घातें
- सबसे महत्वपूर्ण सूत्र (यह केवल दो संख्याओं के लिए लागू होता है):
![Rendered by QuickLaTeX.com \[HCF(a, b) \times LCM(a, b) = a \times b\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-dde7b26b9a3d686f6a4feef88cc99806_l3.png)
(दो संख्याओं का HCF और LCM का गुणनफल, उन दोनों संख्याओं के गुणनफल के बराबर होता है।)- यह सूत्र उत्तर की जाँच (Verification) करने के लिए बहुत उपयोगी है, जैसा कि आपने अपने चयनित पाठ में देखा है (
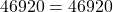 )।
)। - अगर आपको HCF और दोनों संख्याएँ पता हैं, तो आप इस सूत्र से LCM निकाल सकते हैं:
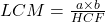
- यह सूत्र उत्तर की जाँच (Verification) करने के लिए बहुत उपयोगी है, जैसा कि आपने अपने चयनित पाठ में देखा है (
- अतिरिक्त तथ्य:
- HCF हमेशा LCM को पूरी तरह विभाजित करता है। (HCF is always a factor of LCM).
- आपके उदाहरण में: 23460, 2 से पूरी तरह विभाज्य है।
MP Board 10th mathematics Real numbers Question Bank
प्र.1. सही विकल्प चुनिये
- 96 और 404 का HCF होगा:
- (a) 120
- (b) 4
- (c) 10
- (d) 3
- उत्तर: (b) 4
- 12 और 15 का HCF होगा:
- (a) 3
- (b) 4
- (c) 10
- (d) 5
- उत्तर: (a) 3
- दो संख्याओं का गुणनफल = 32 तथा उनका LCM = 8 है तो उनका HCF होगा:
- (a) 4
- (b) 8
- (c) 32
- (d) 256
- उत्तर: (a) 4
- 4 और 7 का महत्तम समापवर्तक (HCF) होगा:
- (a) 1
- (b) 2
- (c) 3
- (d) 4
- उत्तर: (a) 1
- संख्याओं 5, 15, 20 के लिए LCM और HCF का अनुपात होगा:
- (a) 9:1
- (b) 4:3
- (c) 11:1
- (d) 12:1
- उत्तर: (d) 12:1
- निम्नलिखित में से कौनसी अपरिमेय संख्या है:
- (a) 2
- (b) 3
- (c) 5
- (d) उपरोक्त सभी
- उत्तर: (d) उपरोक्त सभी
- (a) 2
- 12, 15 और 21 का LCM होगा:
- (a) 180
- (b) 315
- (c) 420
- (d) 252
- उत्तर: (c) 420
- यदि दो संख्याओं का गुणनफल 135 तथा उनका HCF 3 हो तो उनका LCM होगा:
- (a) 45
- (b) 315
- (c) 420
- (d) 135
- उत्तर: (a) 45
- 17, 23 और 29 का HCF होगा:
- (a) 1
- (b) 29
- (c) 23
- (d) 17
- उत्तर: (a) 1
- 11 और 13 का HCF होगा:
- (a) 11
- (b) 13
- (c) 143
- (d) 1
- उत्तर: (d) 1
- 8, 9 और 25 का LCM होगा:
- (a) 72
- (b) 225
- (c) 1800
- (d) 2000
- उत्तर: (c) 1800
- 5−2 कौनसी संख्या है:
- (a) परिमेय
- (b) अपरिमेय
- (c) परिमेय और अपरिमेय दोनों
- (d) उपरोक्त में से कोई नहीं
- उत्तर: (b) अपरिमेय
- 15 और 20 का LCM होगा:
- (a) 60
- (b) 300
- (c) 30
- (d) 90
- उत्तर: (a) 60
प्र.2. रिक्त स्थान की पूर्ति कीजिये
- संख्याओं 8, 9 और 25 के HCF का मान …….. होगा |
- उत्तर: 1
- 2
एक …….. संख्या है |
- उत्तर: अपरिमेय
- 135 और 225 का HCF …….. है |
- उत्तर: 45
- 32
एक …….. संख्या है |
- उत्तर: अपरिमेय
प्र.3. सत्य / असत्य लिखिये
- एक प्राकृत संख्या का अभाज्य गुणनखंडन, उसके गुणनखंडों के क्रम को छोड़ते हुए अद्वितीय होता है |
- उत्तर: सत्य
- प्रत्येक अपरिमेय संख्या एक वास्तविक संख्या होती है |
- उत्तर: सत्य
- प्रत्येक वास्तविक संख्या एक अपरिमेय संख्या होती है |
- उत्तर: असत्य
- 15 और 21 का LCM 105 है |
- उत्तर: सत्य
- 2
1 एक परिमेय संख्या है |
- उत्तर: असत्य
- दो संख्याओं का गुणनफल उनके HCF और LCM के गुणनफल के बराबर होता है |
- उत्तर: सत्य
- 26 और 91 का HCF 13 होगा |
- उत्तर: सत्य
प्र.4. सही जोड़ी मिलाइये
| स्तम्भ – अ | स्तम्भ – ब | उत्तर |
| 1. 306 और 657 का HCF | (i). अपरिमेय | 1. → (iii). 9 |
| 2. 2 | (ii). 27 | 2. → (i). अपरिमेय |
| 3. 9 और 27 का LCM है | (iii). 9 | 3. → (ii). 27 |
प्र.5. एक शब्द / वाक्य में उत्तर दीजिये
- 94 और 404 का HCF लिखिए |
- उत्तर: 2
- संख्या 156 के अभाज्य गुणनखंड लिखिए |
- उत्तर: 22×3×13
- दो प्राकृत संख्याओं के लिए HCF और LCM में क्या संबंध होता है ?
- उत्तर: HCF(a,b)×LCM(a,b)=a×b
- 6, 12 और 30 का LCM कितना होगा ?
- उत्तर: 60
- क्या 5 एक अपरिमेय संख्या है ?
- उत्तर: हाँ
- संख्याओं 8, 9 और 25 का HCF कितना होगा?
- उत्तर: 1
- संख्या 5005 के अभाज्य गुणनखंड लिखिए |
- उत्तर: 5×7×11×13
प्र.6: संख्याओं 135 और 225 का HCF ज्ञात कीजिए।
हल:
हल: अभाज्य गुणनखंडन विधि से:
- 135 के गुणनखंड:
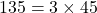
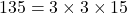
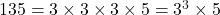
- 225 के गुणनखंड:
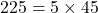
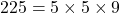
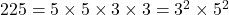
HCF के लिए, हम उभयनिष्ठ (common) गुणनखंडों की सबसे छोटी घात लेते हैं: ![]()
उत्तर: HCF = 45
प्र.7: संख्या 140 को अभाज्य गुणनखंडों के गुणनफल के रूप में व्यक्त कीजिए।
हल:
![]()
![]()
![]()
उत्तर: ![]()
प्र.8: संख्या 156 को अभाज्य गुणनखंडों के गुणनफल के रूप में व्यक्त कीजिए।
हल:
![]()
![]()
![]()
उत्तर: ![]()
प्र.9: संख्या 3825 को अभाज्य गुणनखंडों के गुणनफल के रूप में व्यक्त कीजिए।
हल:
![]()
![]()
![]()
![]()
उत्तर: ![]()
प्र.10: संख्या 7429 को अभाज्य गुणनखंडों के गुणनफल के रूप में व्यक्त कीजिए।
हल:
(यह 17 से विभाज्य है)
![]()
(437, 19 से विभाज्य है)
![]()
उत्तर: ![]()
प्र.11: संख्याओं 9 और 25 का अभाज्य गुणनखंडन विधि से HCF ज्ञात कीजिए।
हल:
![]()
![]()
इन दोनों में कोई उभयनिष्ठ अभाज्य गुणनखंड नहीं है।
उत्तर: HCF = 1
प्र.16: …जाँच कीजिए कि क्या n का कोई मान है… जिसके लिए 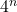 अंक शून्य (0) पर समाप्त होता है।
अंक शून्य (0) पर समाप्त होता है।
हल:
यदि कोई संख्या अंक 0 पर समाप्त होती है, तो वह 10 से विभाज्य होनी चाहिए। इसका मतलब है कि उसके अभाज्य गुणनखंड में 2 और 5 दोनों होने चाहिए।
![]() के गुणनखंड करने पर:
के गुणनखंड करने पर:
![]()
![]() के अभाज्य गुणनखंड में केवल 2 है, 5 नहीं है।
के अभाज्य गुणनखंड में केवल 2 है, 5 नहीं है।
उत्तर: ![]() के किसी भी प्राकृत मान के लिए
के किसी भी प्राकृत मान के लिए ![]() अंक 0 पर समाप्त नहीं हो सकता।
अंक 0 पर समाप्त नहीं हो सकता।
प्र.17: सिद्ध कीजिए कि  एक अपरिमेय संख्या है।
एक अपरिमेय संख्या है।
हल:
हम इसे विरोधाभास (contradiction) द्वारा सिद्ध करेंगे।
- मान लीजिए
 एक परिमेय संख्या है।
एक परिमेय संख्या है। - तो, हम
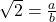 लिख सकते हैं, जहाँ
लिख सकते हैं, जहाँ  और
और  सह-अभाज्य पूर्णांक हैं (अर्थात,
सह-अभाज्य पूर्णांक हैं (अर्थात,  और
और  में 1 के अलावा कोई उभयनिष्ठ गुणनखंड नहीं है) और
में 1 के अलावा कोई उभयनिष्ठ गुणनखंड नहीं है) और 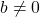 .
. 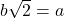
- दोनों पक्षों का वर्ग करने पर:
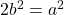 .
. - इसका अर्थ है कि
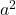 , 2 से विभाज्य है। यदि
, 2 से विभाज्य है। यदि 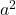 , 2 से विभाज्य है, तो
, 2 से विभाज्य है, तो  भी 2 से विभाज्य होगा।
भी 2 से विभाज्य होगा। - तो, हम
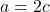 लिख सकते हैं (जहाँ
लिख सकते हैं (जहाँ  कोई पूर्णांक है)।
कोई पूर्णांक है)।  का यह मान समीकरण (4) में रखने पर:
का यह मान समीकरण (4) में रखने पर: 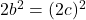 =>
=> 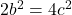 =>
=> 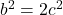 .
.- इसका अर्थ है कि
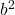 , 2 से विभाज्य है, इसलिए
, 2 से विभाज्य है, इसलिए  भी 2 से विभाज्य होगा।
भी 2 से विभाज्य होगा। - बिंदु (5) और (8) से,
 और
और  दोनों 2 से विभाज्य हैं।
दोनों 2 से विभाज्य हैं। - यह हमारी प्रारंभिक मान्यता (बिंदु 2) का खंडन करता है कि
 और
और  सह-अभाज्य हैं।
सह-अभाज्य हैं। - यह विरोधाभास हमारी गलत कल्पना के कारण हुआ है।अतः,
 एक अपरिमेय संख्या है।
एक अपरिमेय संख्या है।
प्र.18: सिद्ध कीजिए कि  एक अपरिमेय संख्या है।
एक अपरिमेय संख्या है।
हल:
(यह हल प्र.17 के समान है)
- मान लीजिए
 एक परिमेय संख्या है,
एक परिमेय संख्या है, 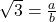 (जहाँ
(जहाँ 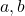 सह-अभाज्य हैं,
सह-अभाज्य हैं, 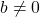 ).
). 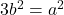 .
.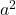 , 3 से विभाज्य है, इसलिए
, 3 से विभाज्य है, इसलिए  भी 3 से विभाज्य है।
भी 3 से विभाज्य है।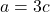 मान रखने पर:
मान रखने पर: 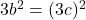 =>
=> 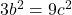 =>
=> 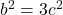 .
.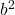 , 3 से विभाज्य है, इसलिए
, 3 से विभाज्य है, इसलिए  भी 3 से विभाज्य है।
भी 3 से विभाज्य है। और
और  दोनों का एक उभयनिष्ठ गुणनखंड 3 है, जो हमारी सह-अभाज्य की मान्यता का खंडन करता है।अतः,
दोनों का एक उभयनिष्ठ गुणनखंड 3 है, जो हमारी सह-अभाज्य की मान्यता का खंडन करता है।अतः,  एक अपरिमेय संख्या है।
एक अपरिमेय संख्या है।
प्र.19: सिद्ध कीजिए कि 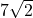 एक अपरिमेय संख्या है।
एक अपरिमेय संख्या है।
हल:
- मान लीजिए
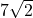 एक परिमेय संख्या है।
एक परिमेय संख्या है। - तो,
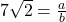 (जहाँ
(जहाँ 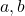 पूर्णांक हैं,
पूर्णांक हैं, 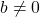 ).
). 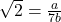 .
.- चूँकि
 ,
,  और 7 पूर्णांक हैं,
और 7 पूर्णांक हैं, 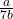 एक परिमेय संख्या होगी।
एक परिमेय संख्या होगी। - इसका अर्थ है कि
 भी एक परिमेय संख्या है।
भी एक परिमेय संख्या है। - लेकिन यह इस तथ्य का खंडन करता है कि
 एक अपरिमेय संख्या है।अतः,
एक अपरिमेय संख्या है।अतः, 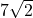 एक अपरिमेय संख्या है।
एक अपरिमेय संख्या है।
प्र.20: संख्या 4, 16 और 20 HCF ज्ञात कीजिए।
हल:
![]()
![]()
![]()
HCF (उभयनिष्ठ गुणनखंड की सबसे छोटी घात) = ![]()
उत्तर: HCF = 4
प्र.21: HCF (306, 657) = 9 दिया है | LCM (306, 657) ज्ञात कीजिए।
हल:
हम जानते हैं: ![]()
![]()
![]()
![]()
![]()
उत्तर: LCM = 22338
प्र.22: 13 और 39 का HCF और LCM ज्ञात कीजिए।
हल:
![]()
![]()
![]()
![]()
उत्तर: HCF = 13, LCM = 39
प्र.23: संख्याओं 6 और 20 का अभाज्य गुणनखंडन विधि से HCF और LCM ज्ञात कीजिए।
हल:
![]()
![]()
HCF (उभयनिष्ठ, छोटी घात) = ![]()
LCM (सभी, बड़ी घात) = ![]()
उत्तर: HCF = 2, LCM = 60
प्र.24: संख्याओं 6, 72 और 120 का अभाज्य गुणनखंडन विधि से HCF और LCM ज्ञात कीजिए।
हल:
![]()
![]()
![]()
HCF (उभयनिष्ठ, छोटी घात) = ![]()
LCM (सभी, बड़ी घात) = ![]()
उत्तर: HCF = 6, LCM = 360
प्र.25: …पूर्णांकों 12, 15 और 21 के HCF और LCM ज्ञात कीजिए।
हल:
![]()
![]()
![]()
HCF (उभयनिष्ठ) = ![]()
LCM (सभी, बड़ी घात) = ![]()
उत्तर: HCF = 3, LCM = 420
प्र.26: व्याख्या कीजिए कि 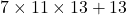 और
और 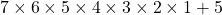 भाज्य संख्याएँ क्यों हैं?
भाज्य संख्याएँ क्यों हैं?
हल:
भाज्य संख्याएँ वे होती हैं जिनके 1 और स्वयं के अलावा भी गुणनखंड होते हैं।
- पहली संख्या:
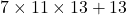 इसमें से 13 कॉमन लेने पर:
इसमें से 13 कॉमन लेने पर: 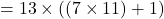
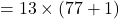
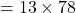 चूंकि इस संख्या का एक गुणनखंड 13 (और 78) है, यह एक भाज्य संख्या है।
चूंकि इस संख्या का एक गुणनखंड 13 (और 78) है, यह एक भाज्य संख्या है। - दूसरी संख्या:
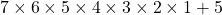 इसमें से 5 कॉमन लेने पर:
इसमें से 5 कॉमन लेने पर: 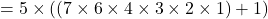
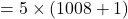
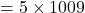 चूंकि इस संख्या का एक गुणनखंड 5 (और 1009) है, यह एक भाज्य संख्या है।
चूंकि इस संख्या का एक गुणनखंड 5 (और 1009) है, यह एक भाज्य संख्या है।
प्र.27: दर्शाइए कि 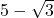 एक अपरिमेय संख्या है?
एक अपरिमेय संख्या है?
हल:
मान लीजिए ![]() एक परिमेय संख्या है।
एक परिमेय संख्या है।
तो, ![]() (जहाँ
(जहाँ ![]() पूर्णांक हैं,
पूर्णांक हैं, ![]() ).
).
![]() को एक तरफ करने पर:
को एक तरफ करने पर:![]()
![]()
चूँकि ![]() ,
, ![]() और 5 पूर्णांक हैं,
और 5 पूर्णांक हैं, ![]() एक परिमेय संख्या होगी।
एक परिमेय संख्या होगी।
इसका अर्थ है कि ![]() भी एक परिमेय संख्या है।
भी एक परिमेय संख्या है।
लेकिन यह इस तथ्य का खंडन करता है कि ![]() एक अपरिमेय संख्या है।
एक अपरिमेय संख्या है।
अतः, ![]() एक अपरिमेय संख्या है।
एक अपरिमेय संख्या है।
- प्र.28: …96 और 404 का HCF ज्ञात कीजिए और फिर इनका LCM ज्ञात कीजिए।
हल:
HCF:![]()
![]()
HCF (उभयनिष्ठ, छोटी घात) = ![]()
LCM:
हम सूत्र का उपयोग कर सकते हैं: ![]()
![]()
![]()
![]()
उत्तर: HCF = 4, LCM = 9696
- उत्तर: HCF = 4, LCM = 9696
प्र.29: संख्याओं 26 और 91 के HCF और LCM ज्ञात कीजिए तथा जाँच कीजिए…
हल:
HCF और LCM:![]()
![]()
HCF = 13
LCM = ![]()
जाँच:
दो संख्याओं का गुणनफल = ![]()
![]()
अतः, ![]() (सत्यापित)
(सत्यापित)
- प्र.30: संख्याओं 510 और 92 के HCF और LCM ज्ञात कीजिए तथा जाँच कीजिए…
हल:
HCF और LCM:![]()
![]()
HCF (उभयनिष्ठ, छोटी घात) = ![]()
LCM (सभी, बड़ी घात) = ![]()
जाँच:
दो संख्याओं का गुणनफल = ![]()
![]()
अतः, ![]() (सत्यापित)
(सत्यापित)
- प्र.31: संख्याओं 17, 23 और 29 का … HCF और LCM ज्ञात कीजिए।
हल:
![]() (अभाज्य)
(अभाज्य)
![]() (अभाज्य)
(अभाज्य)
![]() (अभाज्य)
(अभाज्य)
- HCF:चूँकि ये तीनों अभाज्य संख्याएँ हैं, इनमें कोई उभयनिष्ठ गुणनखंड (1 के अलावा) नहीं है।HCF = 1
- LCM:LCM इनका गुणनफल होगा।
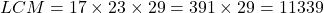
उत्तर: HCF = 1, LCM = 11339