MP Board 10th Graphical method of solving a pair of linear equations : यहाँ अध्याय 3.3: रैखिक समीकरण युग्म का ग्राफीय विधि से हल का सारांश और महत्वपूर्ण नोट्स दिए गए हैं। यह नोट्स आपकी परीक्षा की तैयारी के लिए उपयोगी हैं।
3.3 रैखिक समीकरण युग्म का ग्राफीय विधि से हल
जब हम दो चरों वाले रैखिक समीकरण युग्म (जैसे ![]() और
और ![]() ) को ग्राफ पर निरूपित करते हैं, तो हमें दो सीधी रेखाएँ प्राप्त होती हैं।
) को ग्राफ पर निरूपित करते हैं, तो हमें दो सीधी रेखाएँ प्राप्त होती हैं।
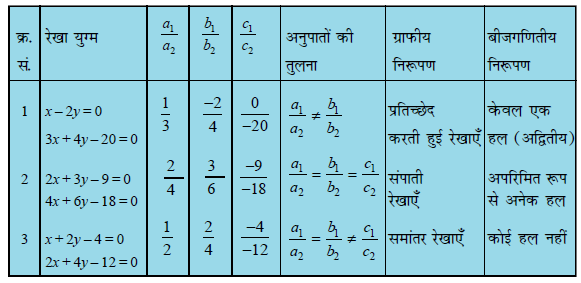
इन दो रेखाओं की स्थिति के आधार पर, हमें तीन प्रकार के हल मिल सकते हैं। हम गुणांकों के अनुपातों की तुलना करके बिना ग्राफ बनाए भी हल की प्रकृति का पता लगा सकते हैं।
प्रश्नावली 3.1: हल
1. आफताब और उसकी पुत्री की आयु
प्रश्न: आफताब अपनी पुत्री से कहता है, ‘सात वर्ष पूर्व मैं तुमसे सात गुनी आयु का था। अब से 3 वर्ष बाद मैं तुमसे केवल तीन गुनी आयु का रह जाऊँगा।’ इस स्थिति को बीजगणितीय एवं ग्राफीय रूपों में व्यक्त कीजिए।
(a) बीजगणितीय निरूपण
- चरण 1: चर मान लीजिए।
- माना आफताब की वर्तमान आयु =
 वर्ष
वर्ष - माना उसकी पुत्री की वर्तमान आयु =
 वर्ष
वर्ष
- माना आफताब की वर्तमान आयु =
- चरण 2: पहली शर्त (“सात वर्ष पूर्व…”)
- 7 वर्ष पूर्व आफताब की आयु =

- 7 वर्ष पूर्व पुत्री की आयु =
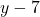
- समीकरण:
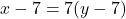
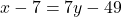
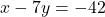 — (1)
— (1)
- 7 वर्ष पूर्व आफताब की आयु =
- चरण 3: दूसरी शर्त (“अब से 3 वर्ष बाद…”)
- 3 वर्ष बाद आफताब की आयु =
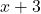
- 3 वर्ष बाद पुत्री की आयु =
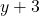
- समीकरण:
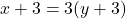
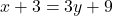
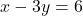 — (2)
— (2)
- 3 वर्ष बाद आफताब की आयु =
(b) ग्राफीय निरूपण
हम ग्राफ बनाने के लिए दोनों समीकरणों से बिंदु ज्ञात करते हैं।
- समीकरण (1) के लिए बिंदु (
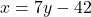 ):
):
- यदि
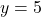 , तो
, तो 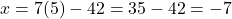
 बिंदु A =
बिंदु A = 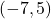
- यदि
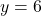 , तो
, तो 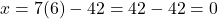
 बिंदु B =
बिंदु B = 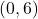
- यदि
- समीकरण (2) के लिए बिंदु (
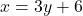 ):
):
- यदि
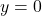 , तो
, तो 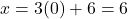
 बिंदु C =
बिंदु C = 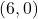
- यदि
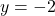 , तो
, तो 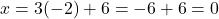
 बिंदु D =
बिंदु D = 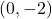
- यदि
ग्राफ का निरूपण:
जब आप इन बिंदुओं (A, B, C, D) को एक ग्राफ पेपर पर आलेखित करेंगे, तो आप देखेंगे कि ये दो रेखाएँ एक-दूसरे को प्रतिच्छेद (intersecting) करती हैं।
(नोट: आपको इन बिंदुओं का उपयोग करके ग्राफ स्वयं बनाना होगा और उसे अपने ब्लॉग पोस्ट में एक छवि (Image) के रूप में अपलोड करना होगा।)
2. क्रिकेट टीम: बल्ले और गेंद
प्रश्न: क्रिकेट टीम के एक कोच ने ₹ 3900 में 3 बल्ले तथा 6 गेंदें खरीदीं। बाद में उसने एक और बल्ला तथा उसी प्रकार की 3 गेंदें ₹ 1300 में खरीदीं। इस स्थिति को बीजगणितीय तथा ज्यामितीय रूपों में व्यक्त कीजिए।
(a) बीजगणितीय निरूपण
- चरण 1: चर मान लीजिए।
- माना 1 बल्ले का मूल्य = ₹

- माना 1 गेंद का मूल्य = ₹

- माना 1 बल्ले का मूल्य = ₹
- चरण 2: पहली शर्त (3 बल्ले, 6 गेंदें)
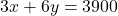
- (3 से भाग देकर सरल करने पर)
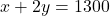 — (1)
— (1)
- चरण 3: दूसरी शर्त (1 बल्ला, 3 गेंदें)
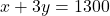 — (2)
— (2)
(b) ग्राफीय निरूपण
- समीकरण (1) के लिए बिंदु (
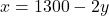 ):
):
- यदि
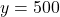 , तो
, तो 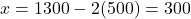
 बिंदु A =
बिंदु A = 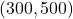
- यदि
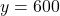 , तो
, तो 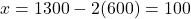
 बिंदु B =
बिंदु B = 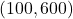
- यदि
- समीकरण (2) के लिए बिंदु (
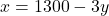 ):
):
- यदि
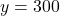 , तो
, तो 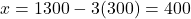
 बिंदु C =
बिंदु C = 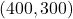
- यदि
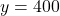 , तो
, तो 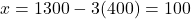
 बिंदु D =
बिंदु D = 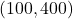
- यदि
ग्राफ का निरूपण:
ये रेखाएँ भी प्रतिच्छेदी (intersecting) हैं। (आप ग्राफ बनाकर इसे देख सकते हैं)।
3. सेब और अंगूर का मूल्य
प्रश्न: 2 kg सेब और 1 kg अंगूर का मूल्य किसी दिन ₹ 160 था। एक महीने बाद 4 kg सेब और 2 kg अंगूर का मूल्य ₹ 300 हो जाता है। इस स्थिति को बीजगणितीय तथा ज्यामितीय रूपों में व्यक्त कीजिए।
(a) बीजगणितीय निरूपण
- चरण 1: चर मान लीजिए।
- माना 1 kg सेब का मूल्य = ₹

- माना 1 kg अंगूर का मूल्य = ₹

- माना 1 kg सेब का मूल्य = ₹
- चरण 2: पहली शर्त (2kg सेब, 1kg अंगूर)
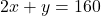 — (1)
— (1)
- चरण 3: दूसरी शर्त (4kg सेब, 2kg अंगूर)
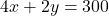
- (2 से भाग देकर सरल करने पर)
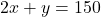 — (2)
— (2)
(b) ग्राफीय निरूपण
- समीकरण (1) के लिए बिंदु (
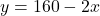 ):
):
- यदि
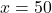 , तो
, तो 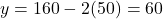
 बिंदु A =
बिंदु A = 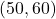
- यदि
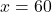 , तो
, तो 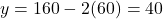
 बिंदु B =
बिंदु B = 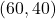
- यदि
- समीकरण (2) के लिए बिंदु (
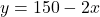 ):
):
- यदि
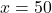 , तो
, तो 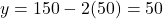
 बिंदु C =
बिंदु C = 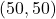
- यदि
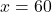 , तो
, तो 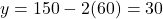
 बिंदु D =
बिंदु D = 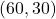
- यदि
ग्राफ का निरूपण:
जब आप इन बिंदुओं को ग्राफ पर आलेखित करेंगे, तो आप देखेंगे कि ये दो रेखाएँ समांतर (parallel) हैं (क्योंकि उनके गुणांक ![]() की शर्त को पूरा करते हैं)।
की शर्त को पूरा करते हैं)।