MP Board 10th Pair of linear equations in two variables : अध्याय 3: दो चर वाले रैखिक समीकरण युग्म की भूमिका और एक महत्वपूर्ण उदाहरण पर आधारित नोट्स
अध्याय 3: दो चर वाले रैखिक समीकरण युग्म (MP Board 10th Pair of linear equations in two variables)
3.1 भूमिका (Introduction)
हम अपनी रोजमर्रा की जिंदगी में कई ऐसी स्थितियों का सामना करते हैं, जिन्हें हम दो चरों (variables) वाले रैखिक समीकरणों के जोड़े (pair) के रूप में दिखा सकते हैं।
एक स्थिति का बीजीय निरूपण (Algebraic Representation of a Situation)
आइए एक उदाहरण से समझें:
समस्या:
अखिला अपने गाँव के मेले में गई। वह चरखी (Giant Wheel) की सवारी करना और हूपला (Hoopla) खेल खेलना चाहती थी।
- स्थिति 1 (शर्त 1): जितनी बार उसने हूपला खेला, वह संख्या उससे आधी बार है जितनी बार उसने चरखी की सवारी की।
- स्थिति 2 (शर्त 2): प्रत्येक बार चरखी की सवारी के लिए ₹3 तथा प्रत्येक बार हूपला खेलने के लिए ₹4 खर्च करने पड़े।
- कुल खर्च: उसने कुल ₹20 खर्च किए।
हमें ज्ञात करना है कि उसने कितनी बार चरखी की सवारी की और कितनी बार हूपला खेला।
समस्या का हल (समीकरण बनाना)
हम इस स्थिति को कक्षा IX के ज्ञान का उपयोग करके दो चरों वाले रैखिक समीकरणों द्वारा निरूपित कर सकते हैं।
चरण 1: चरों को परिभाषित करना
- माना, अखिला द्वारा की गई चरखी की सवारी की संख्या =

- माना, उसके द्वारा हूपला खेलने की संख्या =

चरण 2: स्थितियों को समीकरणों में बदलना
अब दी गई दो स्थितियों को हम समीकरणों द्वारा व्यक्त कर सकते हैं:
- स्थिति 1 के अनुसार: “हूपला खेलने की संख्या (
 )” , “चरखी की सवारी की संख्या (
)” , “चरखी की सवारी की संख्या ( )” की आधी है।
)” की आधी है।
— (1)![Rendered by QuickLaTeX.com \[y = \frac{1}{2}x\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-30f166a52fad9bc83dcad3d8138c2b56_l3.png)
- स्थिति 2 के अनुसार: ₹3 प्रति सवारी (
 बार) और ₹4 प्रति खेल (
बार) और ₹4 प्रति खेल ( बार) का कुल खर्च ₹20 है।
बार) का कुल खर्च ₹20 है।
— (2)![Rendered by QuickLaTeX.com \[3x + 4y = 20\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-e5b5cf495d27947473f10c35770d1799_l3.png)
निष्कर्ष:
हमें दो चरों (![]() और
और ![]() ) में दो रैखिक समीकरणों का एक युग्म (pair) प्राप्त होता है:
) में दो रैखिक समीकरणों का एक युग्म (pair) प्राप्त होता है:
इस अध्याय में, हम ![]() और
और ![]() के मान ज्ञात करने के लिए ऐसे समीकरण युग्मों को हल करने की विभिन्न विधियों का अध्ययन करेंगे।
के मान ज्ञात करने के लिए ऐसे समीकरण युग्मों को हल करने की विभिन्न विधियों का अध्ययन करेंगे।
यहाँ अध्याय 3.2: दो चरों में रैखिक समीकरण युग्म के मुख्य बिंदुओं पर आधारित छात्र-उपयोगी नोट्स दिए गए हैं।
3.2 दो चरों में रैखिक समीकरण युग्म
1. दो चरों वाला रैखिक समीकरण (रिवीजन)
- परिभाषा (Definition): कोई भी समीकरण जिसे
 के रूप में लिखा जा सकता है, जहाँ
के रूप में लिखा जा सकता है, जहाँ  ,
,  , और
, और  वास्तविक संख्याएँ हैं, और
वास्तविक संख्याएँ हैं, और  और
और  दोनों एक साथ शून्य नहीं हैं (इसे
दोनों एक साथ शून्य नहीं हैं (इसे 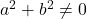 के रूप में भी दर्शाया जाता है)।
के रूप में भी दर्शाया जाता है)। - उदाहरण:

2. समीकरण का हल (Solution of an Equation)
- बीजगणितीय अर्थ (Algebraic Meaning):
 और
और  के मानों का एक युग्म, जैसे
के मानों का एक युग्म, जैसे 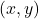 , जो समीकरण को संतुष्ट करता है (यानी, जिसे समीकरण में रखने पर बायाँ पक्ष (LHS) = दायाँ पक्ष (RHS) हो जाता है)।
, जो समीकरण को संतुष्ट करता है (यानी, जिसे समीकरण में रखने पर बायाँ पक्ष (LHS) = दायाँ पक्ष (RHS) हो जाता है)।
- उदाहरण:
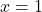 और
और 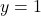 समीकरण
समीकरण  का एक हल है।
का एक हल है। - जाँच: बायाँ पक्ष =
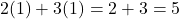 , जो दाएँ पक्ष (RHS) के बराबर है।
, जो दाएँ पक्ष (RHS) के बराबर है। 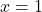 और
और 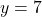 इसका हल नहीं है, क्योंकि
इसका हल नहीं है, क्योंकि 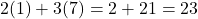 , जो
, जो 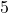 के बराबर नहीं है।
के बराबर नहीं है।
- उदाहरण:
- ज्यामितीय अर्थ (Geometric Meaning): 🤓
- कक्षा IX में हमने सीखा कि दो चरों वाले रैखिक समीकरण का ग्राफ (ज्यामितीय निरूपण) एक सरल रेखा (straight line) होता है।
- समीकरण का प्रत्येक हल
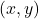 उस समीकरण को निरूपित करने वाली रेखा पर स्थित एक बिंदु होता है।
उस समीकरण को निरूपित करने वाली रेखा पर स्थित एक बिंदु होता है। - (जैसे, बिंदु
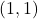 रेखा
रेखा  पर स्थित है, लेकिन बिंदु
पर स्थित है, लेकिन बिंदु 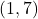 इस पर स्थित नहीं है)।
इस पर स्थित नहीं है)।
3. रैखिक समीकरण युग्म (Pair of Linear Equations)
- परिभाषा: जब हम एक ही दो चरों (
 और
और  ) में दो रैखिक समीकरणों को एक साथ लेते हैं, तो इसे रैखिक समीकरण युग्म (या रैखिक समीकरणों का एक निकाय) कहते हैं।
) में दो रैखिक समीकरणों को एक साथ लेते हैं, तो इसे रैखिक समीकरण युग्म (या रैखिक समीकरणों का एक निकाय) कहते हैं। - व्यापक रूप (General Form):
![Rendered by QuickLaTeX.com \[a_1x + b_1y + c_1 = 0\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-3556ddaab2b19c33b09ab2af065423a9_l3.png)
![Rendered by QuickLaTeX.com \[a_2x + b_2y + c_2 = 0\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-a95bfae9a3a48d5bf8e69f1e52e32963_l3.png)
- जहाँ
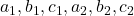 सभी वास्तविक संख्याएँ हैं और
सभी वास्तविक संख्याएँ हैं और 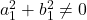 ,
, 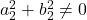 है।
है।
4. समीकरण युग्म का ज्यामितीय निरूपण (Graphical Meaning of a Pair)
- चूँकि एक रैखिक समीकरण एक सरल रेखा को दर्शाता है, इसलिए एक रैखिक समीकरण युग्म ज्यामितीय रूप से दो सरल रेखाओं को निरूपित करता है।
- जब एक तल (plane) में दो रेखाएँ दी गई हों, तो निम्न में से केवल एक ही संभावना हो सकती है:
- प्रतिच्छेद करती रेखाएँ (Intersecting Lines):
- दोनों रेखाएँ केवल एक बिंदु पर प्रतिच्छेद (cut) करती हैं।
- समांतर रेखाएँ (Parallel Lines):
- दोनों रेखाएँ कभी प्रतिच्छेद नहीं करती हैं, अर्थात् वे समांतर हैं।
- संपाती रेखाएँ (Coincident Lines):
- दोनों रेखाएँ एक दूसरे के ठीक ऊपर होती हैं (अर्थात्, वे एक ही रेखा होती हैं)।
- प्रतिच्छेद करती रेखाएँ (Intersecting Lines):
उदाहरण 2 : रोमिला एक स्टेशनरी की दुकान में गई और ₹ 9 में 2 पेंसिल तथा 3 रबड़ खरीदीं। उसकी सहेली सोनाली ने रोमिला के पास नई तरह की पेंसिल और रबड़ देखीं और उसने भी ₹ 18 में उसी तरह की 4 पेंसिल और 6 रबड़ खरीदीं। इस स्थिति को बीजगणितीय तथा ग्राफीय (ज्यामितीय) रूपों में व्यक्त कीजिए।
1. बीजगणितीय निरूपण (Algebraic Representation)
हम इस स्थिति को दो चरों वाले रैखिक समीकरणों के युग्म में व्यक्त करेंगे।
- चरण 1: चर (Variables) को परिभाषित करना
- माना 1 पेंसिल का मूल्य = ₹

- माना 1 रबड़ का मूल्य = ₹

- माना 1 पेंसिल का मूल्य = ₹
- चरण 2: समीकरण बनाना
- स्थिति 1 (रोमिला की खरीद): 2 पेंसिल (
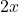 ) और 3 रबड़ (
) और 3 रबड़ (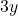 ) का कुल मूल्य ₹9 है।
) का कुल मूल्य ₹9 है।
— (1)![Rendered by QuickLaTeX.com \[2x + 3y = 9\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-883afcf8121195181845503aeff75995_l3.png)
- स्थिति 2 (सोनाली की खरीद): 4 पेंसिल (
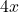 ) और 6 रबड़ (
) और 6 रबड़ (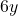 ) का कुल मूल्य ₹18 है।
) का कुल मूल्य ₹18 है।
— (2)![Rendered by QuickLaTeX.com \[4x + 6y = 18\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-4287929f418f237c1a845d506c0e4551_l3.png)
- स्थिति 1 (रोमिला की खरीद): 2 पेंसिल (
अतः, इस स्थिति का बीजगणितीय निरूपण है:
![]()
![]()
2. ग्राफीय (ज्यामितीय) निरूपण (Graphical Representation)
ग्राफ बनाने के लिए, हम दोनों समीकरणों के लिए कम से कम दो हल (बिंदु) ज्ञात करेंगे।
समीकरण (1) के लिए: ![]()
- यदि
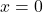 रखने पर,
रखने पर,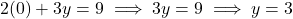 बिंदु A = (0, 3)
बिंदु A = (0, 3) - यदि
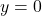 रखने पर,
रखने पर,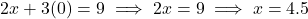 बिंदु B = (4.5, 0)
बिंदु B = (4.5, 0)
समीकरण (2) के लिए: ![]()
(ध्यान दें: यदि हम इस समीकरण को 2 से भाग दें, तो यह ![]() बन जाता है, जो समीकरण (1) ही है।)
बन जाता है, जो समीकरण (1) ही है।)
- यदि
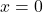 रखने पर,
रखने पर,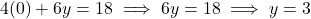 बिंदु C = (0, 3)
बिंदु C = (0, 3) - यदि
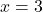 रखने पर,
रखने पर,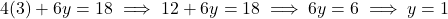 बिंदु D = (3, 1)
बिंदु D = (3, 1)
ग्राफ:
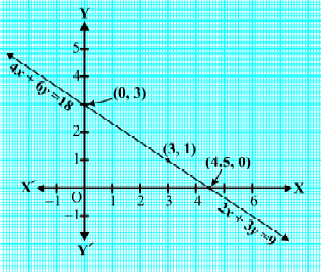
हम ![]() -अक्ष पर पेंसिल का मूल्य और
-अक्ष पर पेंसिल का मूल्य और ![]() -अक्ष पर रबड़ का मूल्य दर्शाते हुए इन बिंदुओं को आलेखित (plot) करेंगे।
-अक्ष पर रबड़ का मूल्य दर्शाते हुए इन बिंदुओं को आलेखित (plot) करेंगे।
निष्कर्ष:
जब हम इन बिंदुओं को ग्राफ पर आलेखित करते हैं, तो हम देखते हैं कि दोनों समीकरणों ( ![]() और
और ![]() ) के सभी बिंदु एक ही रेखा पर स्थित हैं।
) के सभी बिंदु एक ही रेखा पर स्थित हैं।
इसका अर्थ है कि ये रेखाएँ संपाती (coincident) हैं। ज्यामितीय रूप से, यह एक ही रेखा को निरूपित करती हैं और इस स्थिति के अपरिमित रूप से अनेक हल (infinitely many solutions) हैं।
उदाहरण 3: प्रश्न: दो रेल पटरियाँ, समीकरणों 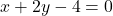 और
और 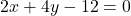 द्वारा निरूपित की गई हैं। इस स्थिति को ज्यामितीय रूप से व्यक्त कीजिए।
द्वारा निरूपित की गई हैं। इस स्थिति को ज्यामितीय रूप से व्यक्त कीजिए।
हल:
यहाँ उदाहरण 3 का बीजगणितीय निरूपण (Algebraic Interpretation) है, जो बिना ग्राफ का उपयोग किए समीकरणों की प्रकृति को दर्शाता है।
प्रश्न: दो रेल पटरियाँ, समीकरणों 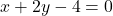 और
और 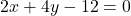 द्वारा निरूपित की गई हैं।
द्वारा निरूपित की गई हैं।
हल:
हम रैखिक समीकरण युग्म ![]() और
और ![]() के गुणांकों (coefficients) के अनुपातों की तुलना करके उनकी प्रकृति ज्ञात कर सकते हैं।
के गुणांकों (coefficients) के अनुपातों की तुलना करके उनकी प्रकृति ज्ञात कर सकते हैं।
दिए गए समीकरण हैं:
गुणांकों की पहचान:
गुणांकों के अनुपातों (Ratios) की गणना:
 =
= 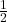
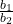 =
= 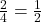
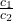 =
= 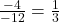
अनुपातों की तुलना:
यहाँ, हम देखते हैं कि:
![]()
(क्योंकि ![]() है, लेकिन
है, लेकिन ![]() है)
है)
निष्कर्ष:
बीजगणितीय नियमों के अनुसार, जब ![]() होता है, तो समीकरण युग्म असंगत (inconsistent) होता है।
होता है, तो समीकरण युग्म असंगत (inconsistent) होता है।
इसका अर्थ है कि इन समीकरणों का कोई हल नहीं है (no solution)। ज्यामितीय रूप से, यह दो समांतर रेखाओं (parallel lines) को निरूपित करता है, जो रेल पटरियों की तरह कभी भी एक-दूसरे को नहीं काटती हैं।
यहाँ प्रश्नावली 3.1 के सभी प्रश्नों का हल
प्रश्न: आफताब अपनी पुत्री से कहता है, ‘सात वर्ष पूर्व मैं तुमसे सात गुनी आयु का था। अब से 3 वर्ष बाद मैं तुमसे केवल तीन गुनी आयु का रह जाऊँगा।’ इस स्थिति को बीजगणितीय एवं ग्राफीय रूपों में व्यक्त कीजिए।
(a) बीजगणितीय निरूपण (Algebraic Representation)
- चरण 1: चर (variables) मान लीजिए।
- माना आफताब की वर्तमान आयु =
 वर्ष
वर्ष - माना उसकी पुत्री की वर्तमान आयु =
 वर्ष
वर्ष
- माना आफताब की वर्तमान आयु =
- चरण 2: पहली शर्त (“सात वर्ष पूर्व…”)
- 7 वर्ष पूर्व आफताब की आयु =

- 7 वर्ष पूर्व पुत्री की आयु =
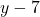
- समीकरण:
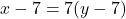
![Rendered by QuickLaTeX.com \[x - 7 = 7y - 49\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-0c34ed6e75741e68e9c8c17767428909_l3.png)
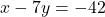 — (1)
— (1)
- 7 वर्ष पूर्व आफताब की आयु =
- चरण 3: दूसरी शर्त (“अब से 3 वर्ष बाद…”)
- 3 वर्ष बाद आफताब की आयु =
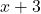
- 3 वर्ष बाद पुत्री की आयु =
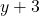
- समीकरण:
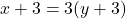
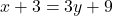
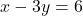 — (2)
— (2)
- 3 वर्ष बाद आफताब की आयु =
(b) ग्राफीय निरूपण (Graphical Representation)
हम दोनों समीकरणों के लिए कुछ बिंदु ज्ञात करते हैं।
- समीकरण (1) के लिए:
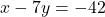 या
या 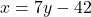
- समीकरण (2) के लिए:
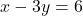 या
या 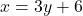
- ग्राफ:इन बिंदुओं को ग्राफ पर आलेखित करने पर, हम देखते हैं कि दोनों रेखाएँ प्रतिच्छेदी (intersecting) हैं।
2. क्रिकेट टीम: बल्ले और गेंद
प्रश्न: क्रिकेट टीम के एक कोच ने ₹ 3900 में 3 बल्ले तथा 6 गेंदें खरीदीं। बाद में उसने एक और बल्ला तथा उसी प्रकार की 3 गेंदें ₹ 1300 में खरीदीं। इस स्थिति को बीजगणितीय तथा ज्यामितीय रूपों में व्यक्त कीजिए।
(a) बीजगणितीय निरूपण
- चरण 1: चर मान लीजिए।
- माना 1 बल्ले का मूल्य = ₹

- माना 1 गेंद का मूल्य = ₹

- माना 1 बल्ले का मूल्य = ₹
- चरण 2: पहली शर्त (3 बल्ले, 6 गेंदें)
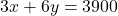
- (3 से भाग देकर सरल करने पर)
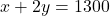 — (1)
— (1)
- चरण 3: दूसरी शर्त (1 बल्ला, 3 गेंदें)
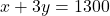 — (2)
— (2)
(b) ग्राफीय निरूपण
- समीकरण (1) के लिए:
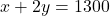 (या
(या 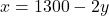 )|
)|  | 500 | 600 || :— | :—: | :—: ||
| 500 | 600 || :— | :—: | :—: ||  | 300 | 100 |
| 300 | 100 | - समीकरण (2) के लिए:
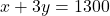 (या
(या 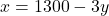 )|
)|  | 300 | 400 || :— | :—: | :—: ||
| 300 | 400 || :— | :—: | :—: ||  | 400 | 100 |
| 400 | 100 | - ग्राफ:दोनों रेखाएँ प्रतिच्छेदी (intersecting) हैं, जो (1300, 0) पर मिलती हैं।
3. सेब और अंगूर का मूल्य
प्रश्न: 2 kg सेब और 1 kg अंगूर का मूल्य किसी दिन ₹ 160 था। एक महीने बाद 4 kg सेब और 2 kg अंगूर का मूल्य ₹ 300 हो जाता है। इस स्थिति को बीजगणितीय तथा ज्यामितीय रूपों में व्यक्त कीजिए।
(a) बीजगणितीय निरूपण
- चरण 1: चर मान लीजिए।
- माना 1 kg सेब का मूल्य = ₹

- माना 1 kg अंगूर का मूल्य = ₹

- माना 1 kg सेब का मूल्य = ₹
- चरण 2: पहली शर्त (2kg सेब, 1kg अंगूर)
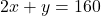 — (1)
— (1)
- चरण 3: दूसरी शर्त (4kg सेब, 2kg अंगूर)
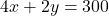
- (2 से भाग देकर सरल करने पर)
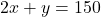 — (2)
— (2)
(b) ग्राफीय निरूपण
- समीकरण (1) के लिए:
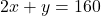 (या
(या 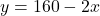 )|
)|  | 50 | 60 || :— | :—: | :—: ||
| 50 | 60 || :— | :—: | :—: ||  | 60 | 40 |
| 60 | 40 | - समीकरण (2) के लिए:
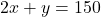 (या
(या 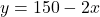 )|
)|  | 50 | 60 || :— | :—: | :—: ||
| 50 | 60 || :— | :—: | :—: ||  | 50 | 30 |
| 50 | 30 | - ग्राफ:दोनों समीकरणों की रेखाएँ समांतर (parallel) हैं, क्योंकि उनका ढलान (slope) एक जैसा है, लेकिन वे
 -अक्ष को अलग-अलग बिंदुओं पर काटती हैं।
-अक्ष को अलग-अलग बिंदुओं पर काटती हैं।