MP Board 9th Mathematics Polynomials Summary: यहाँ अध्याय 2: बहुपद (Polynomials) का सारांश और परीक्षा के लिए महत्वपूर्ण नोट्स दिए गए हैं। इन्हें छात्रों के अध्ययन के लिए व्यवस्थित रूप से समझाया गया है।
अध्याय 2: बहुपद (Polynomials) – मुख्य बिंदु और सारांश
इस अध्याय में आपने बहुपदों के प्रकार, उनके शून्यकों (Zeros) और गुणांकों (Coefficients) के बीच के संबंधों का अध्ययन किया है।
1. बहुपदों के प्रकार (Types of Polynomials)
बहुपद की “घात” (Degree), चर (variable) की उच्चतम घात (highest power) होती है।
- रैखिक बहुपद (Linear Polynomial):
- घात 1 का बहुपद।
- मानक रूप:
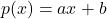 , जहाँ
, जहाँ 
- द्विघात बहुपद (Quadratic Polynomial):
- घात 2 का बहुपद।
- मानक रूप:
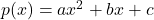 , जहाँ
, जहाँ 
- त्रिघात बहुपद (Cubic Polynomial):
- घात 3 का बहुपद।
- मानक रूप:
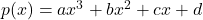 , जहाँ
, जहाँ 
2. बहुपद के शून्यक (Zeros of a Polynomial)
- परिभाषा: चर (
 ) का वह मान, जिसे बहुपद में रखने पर बहुपद का मान शून्य (
) का वह मान, जिसे बहुपद में रखने पर बहुपद का मान शून्य (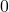 ) हो जाए, शून्यक कहलाता है।
) हो जाए, शून्यक कहलाता है। - ज्यामितीय अर्थ (Geometrical Meaning):
- किसी बहुपद
 के शून्यक उन बिंदुओं के
के शून्यक उन बिंदुओं के  -निर्देशांक (
-निर्देशांक ( -coordinates) होते हैं, जहाँ
-coordinates) होते हैं, जहाँ  का ग्राफ
का ग्राफ  -अक्ष (X-axis) को प्रतिच्छेद (intersect) या स्पर्श (touch) करता है।
-अक्ष (X-axis) को प्रतिच्छेद (intersect) या स्पर्श (touch) करता है।
- शून्यकों की अधिकतम संख्या:
- किसी बहुपद की जितनी घात होती है, उसके अधिक से अधिक उतने ही शून्यक हो सकते हैं।
- एक रैखिक बहुपद का 1 शून्यक होता है।
- एक द्विघात बहुपद के अधिक से अधिक दो शून्यक हो सकते हैं।
- एक त्रिघात बहुपद के अधिक से अधिक तीन शून्यक हो सकते हैं।
- किसी बहुपद
3. शून्यकों और गुणांकों में संबंध (Relationship b/w Zeros & Coefficients)
यह परीक्षा के लिए सबसे महत्वपूर्ण भागों में से एक है।
(i) द्विघात बहुपद के लिए (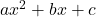 )
)
यदि शून्यक ![]() (अल्फा) और
(अल्फा) और ![]() (बीटा) हों:
(बीटा) हों:
- शून्यकों का योग (Sum of Zeros):
![Rendered by QuickLaTeX.com \[\alpha + \beta = \frac{-b}{a} = \frac{-(x \text{ का गुणांक})}{x^2 \text{ का गुणांक}}\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-080c80ad7b954e2672c510a1d24fbf69_l3.png)
- शून्यकों का गुणनफल (Product of Zeros):
![Rendered by QuickLaTeX.com \[\alpha\beta = \frac{c}{a} = \frac{\text{अचर पद}}{x^2 \text{ का गुणांक}}\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-8647ae51384f534e45e1f4374de78c97_l3.png)
(ii) त्रिघात बहुपद के लिए (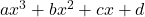 )
)
यदि शून्यक ![]() ,
, ![]() , और
, और ![]() (गामा) हों:
(गामा) हों:
- शून्यकों का योग:
![Rendered by QuickLaTeX.com \[\alpha + \beta + \gamma = \frac{-b}{a} = \frac{-(x^2 \text{ का गुणांक})}{x^3 \text{ का गुणांक}}\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-16b3f36e1b0769bdce0ed1c4325635ea_l3.png)
- शून्यकों को दो-दो करके गुणनफलों का योग:
![Rendered by QuickLaTeX.com \[\alpha\beta + \beta\gamma + \gamma\alpha = \frac{c}{a} = \frac{x \text{ का गुणांक}}{x^3 \text{ का गुणांक}}\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-39fc89fb1a75507520fa800a11e1f0f5_l3.png)
- शून्यकों का गुणनफल:
![Rendered by QuickLaTeX.com \[\alpha\beta\gamma = \frac{-d}{a} = \frac{-(\text{अचर पद})}{x^3 \text{ का गुणांक}}\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-8c460f343d42434f37fc4bae2cd3d6e0_l3.png)
4. बहुपदों के लिए विभाजन एल्गोरिथ्म (Division Algorithm)
यह साधारण यूक्लिड विभाजन (भाज्य = भाजक ![]() भागफल + शेषफल) के जैसा ही है।
भागफल + शेषफल) के जैसा ही है।
- कथन: यदि
 (भाज्य) और
(भाज्य) और 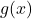 (भाजक) कोई दो बहुपद हैं (जहाँ
(भाजक) कोई दो बहुपद हैं (जहाँ 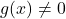 ), तो हमें दो अन्य बहुपद
), तो हमें दो अन्य बहुपद 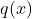 (भागफल) और
(भागफल) और 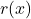 (शेषफल) इस प्रकार प्राप्त होते हैं कि:
(शेषफल) इस प्रकार प्राप्त होते हैं कि:![Rendered by QuickLaTeX.com \[p(x) = g(x) \cdot q(x) + r(x)\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-60dc4f418674b59f8f75d6d1be6f792c_l3.png)
- महत्वपूर्ण शर्त: यह भाग प्रक्रिया तब तक चलती है जब तक:
- या तो शेषफल
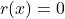 हो जाए,
हो जाए, - अथवा शेषफल
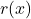 की घात < भाजक
की घात < भाजक 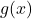 की घात हो जाए।
की घात हो जाए।
- या तो शेषफल
(उपयोग: इसका प्रयोग यह जाँचने के लिए किया जाता है कि ![]() बहुपद
बहुपद ![]() का गुणनखंड है या नहीं। यदि शेषफल
का गुणनखंड है या नहीं। यदि शेषफल ![]() आता है, तो
आता है, तो ![]() एक गुणनखंड होता है।)
एक गुणनखंड होता है।)