1.6 सारांश (Summary)
MP Board 9th Mathematics Chapter 1 Real numbers Summary : इस अध्याय में, आपने निम्नलिखित बिन्दुओं का अध्ययन किया है:
(In this chapter, you have studied the following points:)
- एक संख्या r को परिमेय संख्या कहा जाता है, यदि इसे
 के रूप में लिखा जा सकता हो, जहाँ p और q पूर्णांक हैं और
के रूप में लिखा जा सकता हो, जहाँ p और q पूर्णांक हैं और 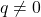 है।(A number r is called a rational number if it can be written in the form
है।(A number r is called a rational number if it can be written in the form  , where p and q are integers and
, where p and q are integers and 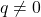 .)
.) - एक संख्या s को अपरिमेय संख्या कहा जाता है, यदि इसे
 के रूप में नहीं लिखा जा सकता हो, जहाँ p और q पूर्णांक हैं और
के रूप में नहीं लिखा जा सकता हो, जहाँ p और q पूर्णांक हैं और 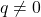 है।(A number s is called an irrational number if it cannot be written in the form
है।(A number s is called an irrational number if it cannot be written in the form  , where p and q are integers and
, where p and q are integers and 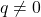 .)
.) - एक परिमेय संख्या का दशमलव प्रसार या तो सांत होता है या अनवसानी आवर्ती होता है। साथ ही, वह संख्या, जिसका दशमलव प्रसार सांत या अनवसानी आवर्ती है, परिमेय होती है।(The decimal expansion of a rational number is either terminating or non-terminating recurring. Conversely, a number whose decimal expansion is terminating or non-terminating recurring is rational.)
- एक अपरिमेय संख्या का दशमलव प्रसार अनवसानी अनावर्ती होता है। साथ ही, वह संख्या जिसका दशमलव प्रसार अनवसानी अनावर्ती है, अपरिमेय होती है।(The decimal expansion of an irrational number is non-terminating non-recurring. Conversely, a number whose decimal expansion is non-terminating non-recurring is irrational.)
- सभी परिमेय और अपरिमेय संख्याओं को एक साथ लेने पर वास्तविक संख्याओं का संग्रह प्राप्त होता है।(The collection of all rational and irrational numbers together make up what we call the collection of real numbers.)
- यदि r परिमेय है और s अपरिमेय है, तब r+s और r-s अपरिमेय संख्याएँ होती हैं तथा rs और
 अपरिमेय संख्याएँ होती हैं यदि
अपरिमेय संख्याएँ होती हैं यदि 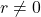 है।(If r is rational and s is irrational, then r+s and r-s are irrational numbers, and rs and
है।(If r is rational and s is irrational, then r+s and r-s are irrational numbers, and rs and  are irrational numbers if
are irrational numbers if 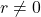 .)
.) - धनात्मक वास्तविक संख्याओं a और b के संबंध में निम्नलिखित सर्वसमिकाएँ लागू होती हैं:(For positive real numbers a and b, the following identities hold:)(i)
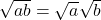 (ii)
(ii) 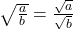 (iii)
(iii) 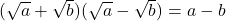 (iv)
(iv) 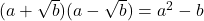 (v)
(v) 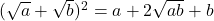
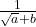 के हर का परिमेयीकरण करने के लिए, इसे हम
के हर का परिमेयीकरण करने के लिए, इसे हम 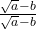 से गुणा करते हैं, जहाँ a और b पूर्णांक हैं।(To rationalize the denominator of
से गुणा करते हैं, जहाँ a और b पूर्णांक हैं।(To rationalize the denominator of 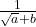 , we multiply this by
, we multiply this by 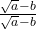 , where a and b are integers.)
, where a and b are integers.)- मान लीजिए a > 0 एक वास्तविक संख्या है और p और q परिमेय संख्याएँ हैं। तब,(Let a > 0 be a real number and p and q be rational numbers. Then,)(i)
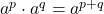 (ii)
(ii) 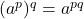 (iii)
(iii) 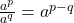 (iv)
(iv)