MP Board 10th Mathematics One Liner part 3 : MP Board 10th Mathematics One Liner Part 3 विद्यार्थियों को बोर्ड परीक्षा की तैयारी में महत्वपूर्ण सहयोग प्रदान करता है। इस भाग में गणित के मुख्य अध्यायों जैसे वृत्तों से संबंधित क्षेत्रफल (Areas Related to Circles), पृष्ठीय क्षेत्रफल और आयतन (Surface Areas and Volumes)
सांख्यिकी (Statistics) और प्रायिकता (Probability) से संबंधित महत्वपूर्ण प्रश्न शामिल किए गए हैं।
MP Board 10th Mathematics One Liner part 3
अध्याय- 11 वृत्तों से संबंधित क्षेत्रफल
अवधारणाओं पर आधारित महत्वपूर्ण तथ्य
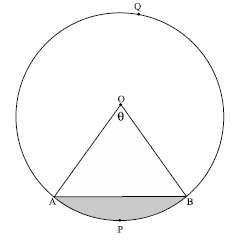
- एक वृत्तीय क्षेत्र का वह भाग जो दो त्रिज्याओं और संगत चाप से घिरा (परिबद्ध) हो, उस वृत्त का एक त्रिज्यखंड कहलाता है।
- वृत्तीय क्षेत्र का वह भाग जो एक जीवा और संगत चाप के बीच में परिबद्ध हो एक वृत्तखंड कहलाता है।
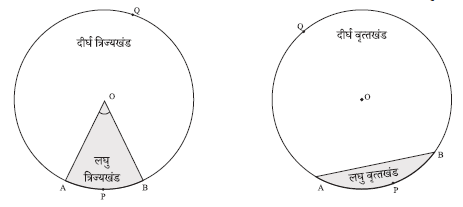
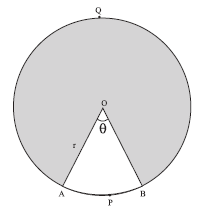
- * अंशीय कोण
 वाले त्रिज्यखंड का क्षेत्रफल
वाले त्रिज्यखंड का क्षेत्रफल 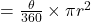 , जहाँ
, जहाँ  वृत्त की त्रिज्या है।
वृत्त की त्रिज्या है। - अंशीय कोण
 वाले त्रिज्यखंड के संगत चाप की लम्बाई
वाले त्रिज्यखंड के संगत चाप की लम्बाई  , जहाँ
, जहाँ  वृत्त की त्रिज्या है।
वृत्त की त्रिज्या है।
दीर्घ त्रिज्यखंड ![]() का क्षेत्रफल
का क्षेत्रफल ![]()
वृत्तखंड का क्षेत्रफल ![]() संगत त्रिज्यखंड का क्षेत्रफल
संगत त्रिज्यखंड का क्षेत्रफल ![]() संगत
संगत ![]() का क्षेत्रफल
का क्षेत्रफल
![]()
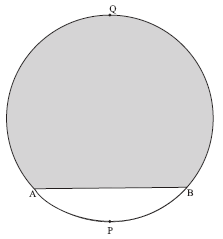
दीर्घ वृत्तखंड ![]() का क्षेत्रफल
का क्षेत्रफल ![]() क्षेत्रफल
क्षेत्रफल ![]() – लघवुत्तृ खडं APB का क्षेत्रफल
– लघवुत्तृ खडं APB का क्षेत्रफल
त्रिज्या ![]() वाले वृत्त का क्षेत्रफल
वाले वृत्त का क्षेत्रफल ![]()
त्रिज्या ![]() वाले वृत्त के एक चतुर्थांश का क्षेत्रफल
वाले वृत्त के एक चतुर्थांश का क्षेत्रफल ![]()
त्रिज्या ![]() वाले वृत्त की परिधि
वाले वृत्त की परिधि ![]()
अध्याय- 12 पृष्ठीय क्षेत्रफल और आयतन
अवधारणाओं पर आधारित महत्वपूर्ण तथ्य
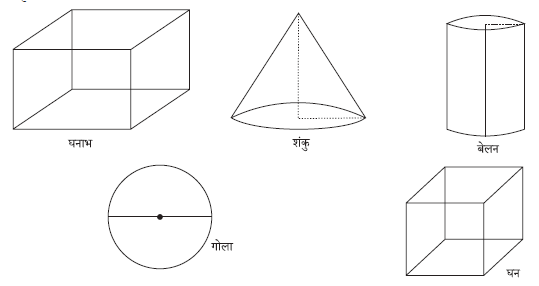
- ठोस आकृतियों के चित्र :
- ठोसों के संयोजन का पृष्ठीय क्षेत्रफल :
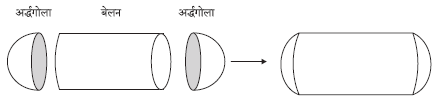
ठोस का सम्पूर्ण पृष्ठीय क्षेत्रफ (TSA) = एक अर्द्धगोले का वक्र पृष्ठीय क्षेत्रफल + बेलन का वक्र पृष्ठीय क्षेत्रफल + दूसरे अर्द्धगोले का वक्र पृष्ठीय क्षेत्रफल
ठोस का सम्पूर्ण पृष्ठीय क्षेत्रफल} =
![]()
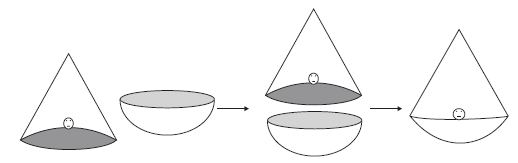
ठोस आकृति का संपूर्ण पृष्ठीय क्षेत्रफल = अर्द्धगोले का वक्र पृष्ठीय क्षेत्रफल + शंकु का वक्र पृष्ठीय क्षेत्रफल
![]()
ब्लॉक का पष्ठीयृ क्षेत्रफल = घन का कु ल पष्ठीयृ क्षेत्रफल – अर्द्धगोले के आधार का क्षे. + अर्द्धगोले का
वक्र पृष्ठीय क्षेत्रफल
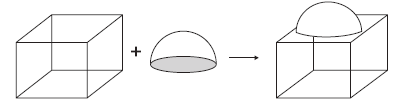
ब्लॉ क का पृष्ठीय क्षेत्रफल = ![]()
ठोसों के सयं ोजन का आयतन :
उदा. अर्द्धबेलन और घनाभ के संयोजन से बनी आकृति
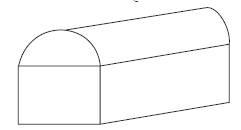
वांछित आयतन} =घनाभ का आयतन +![]() बेलन का आयतन
बेलन का आयतन![]()
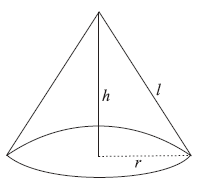
शंकु की तिर्यक ऊँचाई का सूत्र
![]()
जहाँ l = तिर्यक ऊँचाई, h = शंकु की ऊँचाई, r = शंकु की त्रिज्या
अध्याय- 13 सांख्यिकी
अवधारणाओं पर आधारित महत्वपूर्ण तथ्य :-
- दिए हुए प्रेक्षणों का माध्य (या औसत) सभी प्रेक्षणों के मानों के योग को प्रेक्षणों की कुल संख्या से भाग देकर प्राप्त किया जाता है।
![Rendered by QuickLaTeX.com \[\text{माध्य (औसत)} = \frac{\text{सभी प्रेक्षणों का योग}}{\text{प्रेक्षणों की कुल संख्या}}\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-95a7421e954c34d23373b65d943960b4_l3.png)
यदि ![]() प्रेक्षणों की बारंबारताएँ क्रमशः
प्रेक्षणों की बारंबारताएँ क्रमशः ![]() हों तो
हों तो
अर्थात् ![]() बार
बार ![]() बार आता है तो
बार आता है तो
![]()
![]()
![]()
- कल्पित माध्य द्वारा माध्य ज्ञात करना यदि सभी प्रेक्षणों में से मध्य के किसी प्रेक्षण को कल्पित माध्य
 मान लें तथा
मान लें तथा  से प्रत्येक प्रेक्षण का विचलन
से प्रत्येक प्रेक्षण का विचलन 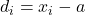 लें तो माध्य
लें तो माध्य![Rendered by QuickLaTeX.com \[\text{माध्य } \bar{x} = a + \frac{\sum_{i=1}^{n} f_{i} d_{i}}{\sum_{i=1}^{n} f_{i}}\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-33946c96e8abc5b01fe37ea10ee2fc57_l3.png)
- पद विचलन विधि –
यदि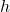 वर्ग अंतराल है तो माध्य
वर्ग अंतराल है तो माध्य![Rendered by QuickLaTeX.com \[\text{माध्य } \bar{x} = a + h \times \left(\frac{\sum_{i=1}^{n} f_{i} u_{i}}{\sum_{i=1}^{n} f_{i}}\right)\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-28104e45f441806dcddad54bb2aba830_l3.png)
जहाँ, कल्पित माध्य है तथा
कल्पित माध्य है तथा 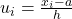 जहाँ,
जहाँ, 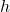 वर्ग अंतराल है।
वर्ग अंतराल है।
- वर्ग अंतराल के उच्च सीमा और निम्न सीमा का मध्यबिंदु वर्ग चिह्न कहलाता है :
![Rendered by QuickLaTeX.com \[\text{वर्ग चिह्न} = \frac{\text{उच्च सीमा} + \text{निम्न सीमा}}{2}\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-88a023035239d33f8f8c097ffd5a8328_l3.png)
- वर्गीकृत आंकड़ों का बहुलक ज्ञात करने के लिए सर्वाधिक (सबसे अधिक बारंबारता) बारंबारता वाले वर्ग को बहुलक वर्ग चुनते हैं।
बहुलक ज्ञात करने हेतु सूत्र![Rendered by QuickLaTeX.com \[\text{बहुलक}=l+\left(\frac{f_{1}-f_{0}}{2 f_{1}-f_{0}-f_{2}}\right) \times h\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-92ea7e44a87c49af6370bf3e50011b3b_l3.png)
l = बहुलक वर्ग की निम्न सीमा - h = वर्ग अन्तराल की माप}
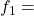 बहुलक वर्ग की बारंबारता
बहुलक वर्ग की बारंबारता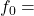 बहुलक वर्ग से ठीक पहले वर्ग की बारंबारता
बहुलक वर्ग से ठीक पहले वर्ग की बारंबारता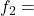 बहुलक वर्ग के ठीक बाद वाले वर्ग की बारंबारता
बहुलक वर्ग के ठीक बाद वाले वर्ग की बारंबारता
- वर्गीकृत आंकड़ों का माध्यक ज्ञात करने के लिए संचयी बारंबारता स्तंभ तैयार करते हैं और सारणी के कुल पदों की प्रकृति सम या विषम के आधार पर माध्यक ज्ञात करते हैं।
वर्गीकृत आंकड़ों का माध्यक ज्ञात करने के लिए सूत्र
- माध्य, माध्यक और बहुलक में सम्बन्ध
3 माध्यक = बहुलक + 2 माध्य - माध्य, माध्यक और बहुलक केन्द्रीय प्रवृत्ति की माप कहलाती है।
- बारंबारता और संचयी बारंबारता केन्द्रीय प्रवृत्ति की माप नहीं है।
अध्याय- 14 प्रायिकता

2 thoughts on “MP Board 10th Mathematics One Liner part 3”