MP Board 12th Mathematics Vector Algebra Question Bank: कक्षा 12 गणित अध्याय-10 सदिश बीजगणित प्रश्न बैंक MP Board 12th Mathematics Vector Algebra Question Bank परिक्षपयोगी प्रश्नो का संग्रह जो परीक्षा मे अत्यंत उपयोगी हैं ।
ज़रूर, यहाँ आपके द्वारा स्कैन किए गए “सदिश बीजगणित” (Vector Algebra) नोट्स का LaTeX/MathJax का उपयोग करके प्रतिलेखन (transcription) दिया गया है:
अध्याय-10 सदिश बीजगणित
स्मरणीय तथ्य (Memorable Facts)
![]() ऐसी राशि जिसमें परिमाण और दिशा दोनों होते हैं, सदिश राशि कहलाती है।
ऐसी राशि जिसमें परिमाण और दिशा दोनों होते हैं, सदिश राशि कहलाती है।
![]() सदिश
सदिश ![]() को
को ![]() या
या ![]() से प्रदर्शित करते हैं।
से प्रदर्शित करते हैं।
![]()
![]() को प्रारम्भिक बिन्दु तथा
को प्रारम्भिक बिन्दु तथा ![]() को अन्तिम बिन्दु कहते हैं।
को अन्तिम बिन्दु कहते हैं।
![]()
![]()
![]() स्थिति सदिश (Position Vector): मूल बिन्दु
स्थिति सदिश (Position Vector): मूल बिन्दु ![]() के सापेक्ष किसी बिन्दु
के सापेक्ष किसी बिन्दु ![]() के निर्देशांक
के निर्देशांक ![]() हैं, तो सदिश
हैं, तो सदिश ![]() को बिन्दु
को बिन्दु ![]() का स्थिति सदिश कहते हैं, जहाँ
का स्थिति सदिश कहते हैं, जहाँ ![]() प्रारम्भिक बिन्दु तथा
प्रारम्भिक बिन्दु तथा ![]() अन्तिम बिन्दु है।
अन्तिम बिन्दु है।
अतः ![]() का स्थिति सदिश
का स्थिति सदिश ![]()
![]()
![]() यदि
यदि ![]() व
व ![]() के स्थिति सदिश क्रमशः
के स्थिति सदिश क्रमशः ![]() व
व ![]() हैं तो
हैं तो ![]()
![]() दिक कोज्या (Direction Cosines): माना
दिक कोज्या (Direction Cosines): माना ![]() ,
, ![]() -अक्ष,
-अक्ष, ![]() -अक्ष एवं
-अक्ष एवं ![]() -अक्ष के साथ क्रमशः
-अक्ष के साथ क्रमशः ![]() एवं
एवं ![]() कोण बनाता है तो
कोण बनाता है तो ![]() को
को ![]() की दिककोज्याएँ कहा जाता है।
की दिककोज्याएँ कहा जाता है।
![]() दिक कोज्याओं को
दिक कोज्याओं को ![]() से प्रदर्शित किया जाता है। अर्थात
से प्रदर्शित किया जाता है। अर्थात
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() शून्य सदिश (zero vector, null vector): वह सदिश जिसका प्रारम्भिक एवं अन्तिम बिन्दु सम्पाती होता है। इसे
शून्य सदिश (zero vector, null vector): वह सदिश जिसका प्रारम्भिक एवं अन्तिम बिन्दु सम्पाती होता है। इसे ![]() से या
से या ![]() आदि से निर्दिष्ट किया जाता है। इसका परिमाण शून्य होता है।
आदि से निर्दिष्ट किया जाता है। इसका परिमाण शून्य होता है।
![]() संरेख सदिश (Collinear Vectors): दो या दो से अधिक सदिश जो एक ही रेखा के समांतर हों, संरेख सदिश कहलाते हैं।
संरेख सदिश (Collinear Vectors): दो या दो से अधिक सदिश जो एक ही रेखा के समांतर हों, संरेख सदिश कहलाते हैं।
![]() समान सदिश (Equal Vector): दो सदिश
समान सदिश (Equal Vector): दो सदिश ![]() तथा
तथा ![]() समान सदिश कहलाते हैं यदि उनके परिमाण एवं दिशा समान है। इन्हें
समान सदिश कहलाते हैं यदि उनके परिमाण एवं दिशा समान है। इन्हें ![]() के रूप में लिखा जाता है।
के रूप में लिखा जाता है।
![]() ऋणात्मक सदिश (Negative of a vector): एक सदिश जिसका परिमाण, दिये हुए सदिश के समान है परन्तु दिशा विपरीत हो ऋणात्मक सदिश कहलाता है। उदाहरण सदिश
ऋणात्मक सदिश (Negative of a vector): एक सदिश जिसका परिमाण, दिये हुए सदिश के समान है परन्तु दिशा विपरीत हो ऋणात्मक सदिश कहलाता है। उदाहरण सदिश ![]() का ऋणात्मक सदिश है।
का ऋणात्मक सदिश है।
![]()
![]()
![]()
![]() अदिश से सदिश का गुणनफल:
अदिश से सदिश का गुणनफल: ![]()
यहाँ ![]() , सदिश
, सदिश ![]() का संरेख है तथा
का संरेख है तथा ![]() का मान धनात्मक या ऋणात्मक होने के अनुसार इसकी दिशा समान या विपरीत होती है।
का मान धनात्मक या ऋणात्मक होने के अनुसार इसकी दिशा समान या विपरीत होती है।
![]() एक सदिश के घटक (Components of a vector):
एक सदिश के घटक (Components of a vector):
यदि ![]() हो तो
हो तो ![]()
![]() के अदिश घटक कहलाते हैं तथा
के अदिश घटक कहलाते हैं तथा ![]() सदिश
सदिश ![]() के सदिश घटक कहलाते हैं।
के सदिश घटक कहलाते हैं।
![]() परस्पर लंबवत इकाई सदिश:
परस्पर लंबवत इकाई सदिश: ![]() परस्पर लंबवत इकाई सदिश हैं।
परस्पर लंबवत इकाई सदिश हैं।
![]() किसी सदिश का परिमाण: यदि
किसी सदिश का परिमाण: यदि ![]() हो तो सदिश
हो तो सदिश ![]() का परिमाण
का परिमाण ![]()
![]() सदिशों के योग का त्रिभुज नियम
सदिशों के योग का त्रिभुज नियम
![]()
![]()
![]() सदिश योगफल के गुणधर्म
सदिश योगफल के गुणधर्म
- क्रम विनिमय नियम का पालन करता है। अर्थात
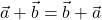
- साहचर्य नियम का पालन करता है। अर्थात
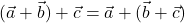
- शून्य सदिश
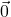 को सदिश योगफल के लिये योज्य सर्वसमिका कहा जाता है। अर्थात
को सदिश योगफल के लिये योज्य सर्वसमिका कहा जाता है। अर्थात 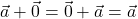
![]() किसी सदिश का इकाई सदिश: किसी सदिश
किसी सदिश का इकाई सदिश: किसी सदिश ![]() का इकाई सदिश
का इकाई सदिश ![]() द्वारा प्रदर्शित किया जाता है तथा
द्वारा प्रदर्शित किया जाता है तथा ![]()
![]() दो बिन्दुओं को मिलाने वाला सदिश:
दो बिन्दुओं को मिलाने वाला सदिश:
यदि ![]() तथा
तथा![]() हो तो
हो तो
![]()
![]()
![]() खण्ड सूत्र (Section Formula): यदि बिन्दु
खण्ड सूत्र (Section Formula): यदि बिन्दु ![]() ,
, ![]() एवं
एवं ![]() को
को ![]() में अंत: विभाजित करता है तो
में अंत: विभाजित करता है तो ![]() का स्थिति सदिश
का स्थिति सदिश ![]() होगा।
होगा।
![]()
![]() यदि बिन्दु
यदि बिन्दु ![]() ,
, ![]() और
और ![]() को बाह्यतः विभाजित करता है तो
को बाह्यतः विभाजित करता है तो ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \[\star \quad \vec{a} \text{ व } \vec{b} \text{ के लम्बवत मात्रक सदिश} = \pm \frac{\vec{a} \times \vec{b}}{|\vec{a} \times \vec{b}|}\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-6e67db6f83412c4f88129da5f567624b_l3.png)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \[\text{समी } \cos\theta = \frac{\vec{a} \cdot \vec{b}}{|\vec{a}| |\vec{b}|} \text{ द्वारा ज्ञात किया जा सकता है।}\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-56215f3fd8f4fff661f6539aab668dc4_l3.png)
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \[\text{या } \frac{|\vec{a} \times \vec{b}|}{|\vec{a}| |\vec{b}|} = \sin\theta\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-c743b864ed458859f14db81332740712_l3.png)
ज़रूर, यहाँ आपके द्वारा स्कैन किए गए बहुविकल्पीय प्रश्नों (Multiple Choice Questions) का LaTeX/MathJax का उपयोग करके प्रतिलेखन (transcription) दिया गया है:
प्रश्न 1. सही विकल्प चुनिए (Choose the correct option)
(i) किसी त्रिभुज ![]() के लिए निम्न में से कौन सा कथन सत्य नहीं है
के लिए निम्न में से कौन सा कथन सत्य नहीं है
(a) ![]()
(b) ![]()
(c) ![]()
(d) ![]()
(ii) यदि ![]() और
और ![]() दो संरेख सदिश हैं तो निम्नलिखित में से कौन सा कथन सत्य है
दो संरेख सदिश हैं तो निम्नलिखित में से कौन सा कथन सत्य है
(a) ![]() किसी अदिश
किसी अदिश ![]() के लिए
के लिए
(b) ![]()
(c) ![]() और
और ![]() के क्रमागत घटक समानुपाती नहीं है
के क्रमागत घटक समानुपाती नहीं है
(d) दोनों सदिशों ![]() तथा
तथा ![]() की दिशा समान है परन्तु परिमाण विभिन्न हैं।
की दिशा समान है परन्तु परिमाण विभिन्न हैं।
(iii) यदि शून्येतर सदिश ![]() का परिमाण
का परिमाण ![]() है और
है और ![]() एक शून्येतर अदिश है तथा
एक शून्येतर अदिश है तथा ![]() एक मात्रक सदिश है यदि :
एक मात्रक सदिश है यदि :
(a) ![]()
(b) ![]()
(c) ![]()
(d) ![]()
(iv) यदि सदिशों ![]() और
और ![]() इस प्रकार हैं कि
इस प्रकार हैं कि ![]() और
और ![]() तब
तब ![]() एक मात्रक सदिश है यदि
एक मात्रक सदिश है यदि ![]() और
और ![]() के बीच का कोण है :
के बीच का कोण है :
(a) ![]()
(b) ![]()
(c) ![]()
(d) ![]()
(v) यदि आयत के शीर्ष ![]() और
और ![]() हैं जिनके स्थिति सदिश क्रमशः
हैं जिनके स्थिति सदिश क्रमशः ![]() ,
, ![]() ,
, ![]() और
और ![]() का क्षेत्रफल है:
का क्षेत्रफल है:
(a) ![]() वर्ग इकाई
वर्ग इकाई
(b) ![]() वर्ग इकाई
वर्ग इकाई
(c) ![]() वर्ग इकाई
वर्ग इकाई
(d) ![]() वर्ग इकाई
वर्ग इकाई
(vi) यदि दो सदिशों ![]() और
और ![]() के बीच कोण
के बीच कोण ![]() हो तो
हो तो ![]() होगा यदि
होगा यदि
(a) ![]()
(b) ![]()
(c) ![]()
(d) ![]()
(vii) यदि दो सदिशों ![]() और
और ![]() दो मात्रक सदिश हैं और उनके बीच का कोण
दो मात्रक सदिश हैं और उनके बीच का कोण ![]() है तो
है तो ![]() एक मात्रक सदिश है यदि
एक मात्रक सदिश है यदि
(a) ![]()
(b) ![]()
(c) ![]()
(d) ![]()
(viii) ![]() का मान है:
का मान है:
(a) ![]()
(b) ![]()
(c) ![]()
(d) ![]()
(ix) यदि दो सदिशों ![]() और
और ![]() के बीच का कोण
के बीच का कोण ![]() हो तो
हो तो ![]() जब
जब ![]() बराबर है :
बराबर है :
(a) ![]()
(b) ![]()
(c) ![]()
(d) ![]()
(x) ![]() की दिशा में इकाई सदिश होगा –
की दिशा में इकाई सदिश होगा –
(a) ![]()
(b) ![]()
(c) ![]()
(d) ![]()
(xi) किसी त्रिभुज ![]() में
में ![]() का मान होगा –
का मान होगा –
(a) ![]()
(b) ![]()
(c) ![]()
(d) ![]()
(xii) यदि ![]() तथा
तथा ![]() हो तो
हो तो ![]() का मान होगा –
का मान होगा –
(a) ![]()
(b) ![]()
(c) ![]()
(d) ![]()
(xiii) निम्न में से शून्य सदिश है –
(a) ![]()
(b) ![]()
(c) ![]()
(d) ![]()
(xiv) ![]() का मान होगा –
का मान होगा –
(a) ![]()
(b) ![]()
(c) ![]()
(d) कुछ नहीं
(xv) ![]() का मान होगा –
का मान होगा –
(a) ![]()
(b) ![]()
(c) ![]()
(d) ![]()
(xvi) ![]() का मान होगा –
का मान होगा –
(a) ![]()
(b) ![]()
(c) ![]()
(d) ![]()
(xvii) यदि ![]() और
और ![]() समान्तर हों तो
समान्तर हों तो ![]() होगा –
होगा –
(a) ![]()
(b) ![]()
(c) ![]()
(d) ![]()
(xviii) ![]() का मान होगा –
का मान होगा –
(a) ![]()
(b) ![]()
(c) ![]()
(d) ![]()
(xix) ![]() को कहते हैं –
को कहते हैं –
(a) दिक-स्थान
(b) दिक कोज्या
(c) कोण
(d) सदिश
(xx) ![]() है एक –
है एक –
(a) सदिश राशि
(b) अदिश राशि
(c) संरेख सदिश
(d) ऋणात्मक सदिश
(xxi) ![]() है एक –
है एक –
(a) सदिश राशि
(b) अदिश राशि
(c) संरेख सदिश
(d) समान सदिश
(xxii) यदि ![]() हो तो सदिश
हो तो सदिश ![]() का परिमाण होगा –
का परिमाण होगा –
(a) ![]()
(b) ![]()
(c) ![]()
(d) ![]()
(xxiii) ![]() का मान होगा –
का मान होगा –
(a) ![]()
(b) ![]()
(c) ![]()
(d) ![]()
(xxiv) दो सदिशों ![]() तथा
तथा ![]() के बीच का कोण होगा –
के बीच का कोण होगा –
(a) ![]()
(b) ![]()
(c) ![]()
(d) इनमें से कोई नहीं
प्रश्न-2 निम्नलिखित में से सत्य/असत्य लिखिए।
i) त्रिभुज की तीनों भुजाओं को एक क्रम में लेने पर उनका सदिश योग 1 होता है।
ii) दिए हुए सदिश ![]() के लिए
के लिए ![]() ,
, ![]() की दिशा में मात्रक सदिश होता है।
की दिशा में मात्रक सदिश होता है।
iii) एक सदिश के सदिश घटक इसके दिक अनुपात कहलाते हैं।
iv) यदि किसी समान्तर चतुर्भुज की संलग्न भुजाएँ ![]() और
और ![]() हैं तो उसका क्षेत्रफल
हैं तो उसका क्षेत्रफल ![]() द्वारा प्राप्त होता है।
द्वारा प्राप्त होता है।
v) यदि ![]() हो तो
हो तो ![]() व
व ![]() के बीच का कोण
के बीच का कोण ![]() होगा।
होगा।
vi) ![]() का मान
का मान ![]() है।
है।
vii) यदि ![]() का मान
का मान ![]() हो तो
हो तो ![]() होगा।
होगा।
viii) यदि ![]() व
व ![]() का स्थिति सदिश
का स्थिति सदिश ![]() व
व ![]() हो तो
हो तो ![]() का मान
का मान ![]() होगा।
होगा।
ix) ![]() का परिमाण
का परिमाण ![]() है।
है।
x) ![]() होता है।
होता है।
xi) समांतर चतुर्भुज का क्षेत्रफल ![]() है।
है।
xii) ![]() और
और ![]() परस्पर लंब हैं।
परस्पर लंब हैं।
xiii) ![]() ,
, ![]() ,
, ![]() हो तो दोनों के बीच का कोण
हो तो दोनों के बीच का कोण ![]() होगा।
होगा।
xiv) ![]() का मान
का मान ![]() होता है।
होता है।
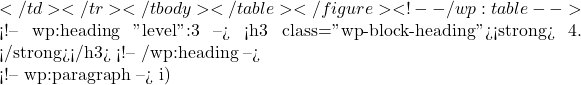 \vec{a}
\vec{a}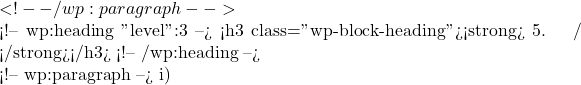 \vec{a}
\vec{a}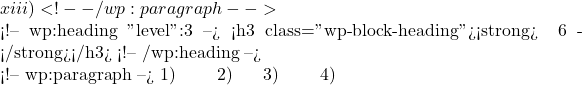 x, y, z
x, y, z |\vec{a}| |\vec{b}|
|\vec{a}| |\vec{b}| |\vec{a} + \vec{b}| \leq |\vec{a}| + |\vec{b}|
|\vec{a} + \vec{b}| \leq |\vec{a}| + |\vec{b}|