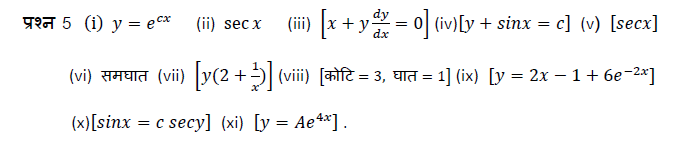MP Board 12th Mathematics Differential Equation Question Bank : कक्षा 12 गणित अध्याय-8 अवकल समीकरण प्रश्न बैंक
अध्याय-8 अवकल समीकरण
स्मरणीय बिन्दु (Important Points)
- वे बीजगणितीय समीकरण जिनमें अवकल गुणांक के पद हों, अवकल समीकरण (differential equation) कहलाते हैं। उदाहरण:
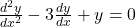
- साधारण अवकल समीकरण (Ordinary differential equation): वह अवकल समीकरण, जिनमें केवल एक ही स्वतंत्र चर है। उदाहरण:
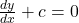
 अवकल समीकरण की कोटि (Order of a diff. equation) किसी अवकल समीकरण में उसके उच्चतम अवकलज की कोटि कहलाती है। उदाहरण:
अवकल समीकरण की कोटि (Order of a diff. equation) किसी अवकल समीकरण में उसके उच्चतम अवकलज की कोटि कहलाती है। उदाहरण: 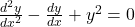 की कोटि
की कोटि  है।
है। अवकल समीकरण की घात (Degree of a diff. equation) किसी अवकल समीकरण में प्रयुक्त अवकलज या अवकल गुणांक भिन्नात्मक घातों तथा करणी चिह्नों से मुक्त हों तब उच्चतम अवकलन की घात, उस समीकरण की घात कहलाती है। उदाहरण:
अवकल समीकरण की घात (Degree of a diff. equation) किसी अवकल समीकरण में प्रयुक्त अवकलज या अवकल गुणांक भिन्नात्मक घातों तथा करणी चिह्नों से मुक्त हों तब उच्चतम अवकलन की घात, उस समीकरण की घात कहलाती है। उदाहरण: 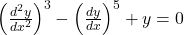 की घात
की घात 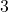 है।
है।
5.  अवकल समीकरण का हल (Solution of a diff. equation):
अवकल समीकरण का हल (Solution of a diff. equation):
किसी अवकल समीकरण का हल अथवा समाकलन चरों में वह सम्बन्ध होता है जिनसे ![]() और जिनसे प्राप्त अवकलजों से समीकरण सन्तुष्ट हो जाए।
और जिनसे प्राप्त अवकलजों से समीकरण सन्तुष्ट हो जाए।
 व्यापक और विशेष हल (General and Particular solution) किसी अवकल समीकरण में उस हल को जिसमें स्वेच्छ अचरों की संख्या, समीकरण की कोटि के बराबर हो व्यापक हल कहते हैं। व्यापक हल में स्वेच्छ अचरों को विशेष मान देने पर प्राप्त हल को विशेष हल कहते हैं।
व्यापक और विशेष हल (General and Particular solution) किसी अवकल समीकरण में उस हल को जिसमें स्वेच्छ अचरों की संख्या, समीकरण की कोटि के बराबर हो व्यापक हल कहते हैं। व्यापक हल में स्वेच्छ अचरों को विशेष मान देने पर प्राप्त हल को विशेष हल कहते हैं। प्रथम कोटि एवं प्रथम घात का अवकल समीकरण:
प्रथम कोटि एवं प्रथम घात का अवकल समीकरण: 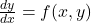 इसे निम्न रूप में भी लिखा जा सकता है:
इसे निम्न रूप में भी लिखा जा सकता है:![Rendered by QuickLaTeX.com \[Mdx + Ndy = 0\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-b37e4ffce7ed7ebdbd97bde69c128706_l3.png)
 समघात अवकल समीकरण (Homogeneous equation):
समघात अवकल समीकरण (Homogeneous equation):![Rendered by QuickLaTeX.com \[\frac{dy}{dx} = \frac{f_1(x, y)}{f_2(x, y)} \quad \text{उदाहरण:}\quad \frac{dy}{dx} = \frac{y-x}{y+x}\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-4cd44650d799c0df7ec0bf2f1cf045de_l3.png)
 रैखिक अवकल समीकरण (Linear diff. equ.): किसी अवकल समीकरण में परतन्त्र चर (माना
रैखिक अवकल समीकरण (Linear diff. equ.): किसी अवकल समीकरण में परतन्त्र चर (माना  ) और उसके अवकलज प्रथम घात के हों तो उसे रैखिक अवकल समीकरण कहते हैं।
) और उसके अवकलज प्रथम घात के हों तो उसे रैखिक अवकल समीकरण कहते हैं। ![Rendered by QuickLaTeX.com \[\frac{dy}{dx} + Py = Q\]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-00b896b892d3eee36e88938badc9462d_l3.png)
जहाँ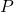 और
और 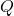 अचर अथवा केवल
अचर अथवा केवल  के फलन हैं। उदाहरण:
के फलन हैं। उदाहरण: 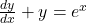 एक रैखिक समीकरण है। इसका हल:
एक रैखिक समीकरण है। इसका हल: 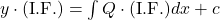 यहाँ I.F. (समाकलन गुणांक)
यहाँ I.F. (समाकलन गुणांक) 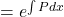
 समघातीय फलन (Homogeneous function):
समघातीय फलन (Homogeneous function):
वह अवकल समीकरण जिसे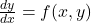 अथवा
अथवा 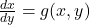 के रूप में व्यक्त किया जा सकता है, जहाँ
के रूप में व्यक्त किया जा सकता है, जहाँ 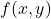 एवं
एवं 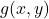 शून्य घात वाले समघातीय फलन हैं, समघातीय अवकल समीकरण कहलाता है। उदाहरण:
शून्य घात वाले समघातीय फलन हैं, समघातीय अवकल समीकरण कहलाता है। उदाहरण: 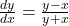
प्रश्न 1- सही विकल्प चुनिए (Choose the correct option)
(i) अवकल समीकरण ![]() की कोटि है।
की कोटि है।
(a) 2
(b) 1
(c) 0
(d) परिभाषित नहीं है।
(ii) अवकल समीकरण ![]() की घात है।
की घात है।
(a) 2
(b) 1
(c) 0
(d) परिभाषित नहीं है।
(iii) ![]() के रूप वाले समघातीय अवकल समीकरण को हल करने के लिए निम्नलिखित में से कौन सा प्रतिस्थापन किया जाता है:
के रूप वाले समघातीय अवकल समीकरण को हल करने के लिए निम्नलिखित में से कौन सा प्रतिस्थापन किया जाता है:
(a) ![]()
(b) ![]()
(c) ![]()
(d) ![]()
(iv) अवकल समीकरण ![]() का समाकलन गुणांक है:
का समाकलन गुणांक है:
(a) ![]()
(b) ![]()
(c) ![]()
(d) ![]()
(v) अवकल समीकरण ![]() की कोटि एवं घात होगी।
की कोटि एवं घात होगी।
(a) 1, 2
(b) 2, 1
(c) 1, 1
(d) 2, 2
(vi) अवकल समीकरण ![]() की कोटि एवं घात होगी।
की कोटि एवं घात होगी।
(a) 1, 2
(b) 2, 1
(c) 1, 3
(d) 3, 1
(vii) अवकल समीकरण ![]() की कोटि एवं घात होगी।
की कोटि एवं घात होगी।
(a) 1, 2
(b) 2, 2
(c) 2, 1
(d) 1, 1
(viii) अवकल समीकरण ![]() की कोटि एवं घात होगी।
की कोटि एवं घात होगी।
(a) 2, 2
(b) 2, 1
(c) 1, 2
(d) 1, 1
(ix) अवकल समीकरण 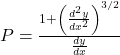 की कोटि एवं घात होगी।
की कोटि एवं घात होगी।
(a) 6, 2
(b) 2, 6
(c) 2, 3
(d) 2, 3/2
(x) रैखिक अवकल समीकरण ![]() का समाकलन गुणांक (I.F.) होगा।
का समाकलन गुणांक (I.F.) होगा।
(a) ![]()
(b) ![]()
(c) ![]()
(d) ![]()
(xi) रैखिक अवकल समीकरण ![]() में
में ![]() एवं
एवं ![]() हैं।
हैं।
(a) अचर अथवा ![]() के फलन
के फलन
(b) अचर ![]() के फलन
के फलन
(d) अचर अथवा ![]() के फलन
के फलन
(xii) रैखिक अवकल समीकरण ![]() में
में ![]() एवं
एवं ![]() हैं।
हैं।
(a) अचर अथवा ![]() के फलन
के फलन
(b) अचर
(c) ![]() के फलन
के फलन
(d) अचर अथवा ![]() के फलन
के फलन
(xiii) रैखिक अवकल समीकरण ![]() का हल है।
का हल है।
(a) ![]()
(b) ![]()
(c) ![]()
(d) ![]()
(xiv) ![]() समीकरण है।
समीकरण है।
(a) समघात
(b) रैखिक
(c) बरनौली
(d) इनमें से कोई नहीं
प्रश्न 2- एक शब्द/वाक्य में उत्तर दीजिये (Answer in one word/sentence)
| क्र.सं. | प्रश्न (Question) |
|---|---|
| (i) | |
| (ii) | अवकल समीकरण |
| (iii) | रैखिक अवकल समीकरण का मानक रूप लिखिए। |
| (iv) | अवकल समीकरण |
| (v) | अवकल समी. |
| (vi) | समी. |
| (vii) | |
| (viii) | समघात समी. का एक उदा. लिखिए। |
| (ix) | रैखिक समी. का एक उदा. लिखिए। |
| (x) | |
| (xi) | |
| (xii) | रैखिक समी. |
| (xiii) | |
| (xiv) | प्रथम कोटि व दो घात वाला अवकल समीकरण लिखिए। |
प्रश्न 3- सही जोड़ी बनाइये (Match the column)
| क्र.सं. | स्तम्भ (A) (Column A) | स्तम्भ (B) (Column B) |
|---|---|---|
| (i) | (अ) समघात अवकल समी. | |
| (ii) | समी. | (ब) |
| (iii) | अवकल समी. | (स) |
| (iv) | अवकल समी. | (द) रैखीय अवकल समी. |
| (v) | अवकल समी. | (ड़) एक |
| (vi) | (फ) | |
| (vii) | (ल) समघात समी. | |
| (viii) | (र) रैखिक समी. |
ज़रूर, यहाँ आपके द्वारा स्कैन किए गए सभी प्रश्नों का LaTeX/MathJax का उपयोग करके बिना हल किए प्रतिलेखन (transcription) दिया गया है:
प्रश्न 4. निम्नलिखित में से सत्य/असत्य लिखिए।
(i) अवकल समीकरण ![]() का व्यापक हल
का व्यापक हल ![]() है।
है।
(ii) ![]() एक समघातीय अवकलन समीकरण नहीं है।
एक समघातीय अवकलन समीकरण नहीं है।
(iii) अवकल समीकरण ![]() का हल
का हल ![]() है।
है।
(iv) ![]() एक रैखिक अवकलन समीकरण नहीं है।
एक रैखिक अवकलन समीकरण नहीं है।
(v) समघात अवकल समी. को हल करने के लिये ![]() मान रखा जाता है।
मान रखा जाता है।
(vi) ![]() को चरों के पृथक्करण द्वारा हल किया जा सकता है।
को चरों के पृथक्करण द्वारा हल किया जा सकता है।
(vii) ![]() का हल
का हल ![]() है।
है।
(viii) ![]() की कोटि एक है।
की कोटि एक है।
(ix) ![]() की घात दो है।
की घात दो है।
(x) ![]() अवकल समी.
अवकल समी. ![]() का एक हल है।
का एक हल है।
(xi) ![]() एक समघात फलन है।
एक समघात फलन है।
(xii) ![]() का समाकलन गुणांक
का समाकलन गुणांक ![]() है।
है।
(xiii) ![]() का समाकलन गुणांक
का समाकलन गुणांक ![]() है।
है।
(xiv) ![]() एक रैखिक समी. है।
एक रैखिक समी. है।
प्रश्न 5. रिक्त स्थानों की पूर्ति कीजिए।
(i) अवकल समीकरण ![]() का हल
का हल ![]() है।
है।
(ii) अवकल समीकरण ![]() ;
; ![]() यदि
यदि ![]() का विशिष्ट हल
का विशिष्ट हल ![]() है।
है।
(iii) अवकल समी. ![]() का हल
का हल ![]() है।
है।
(iv) रैखिक अवकल समी. ![]() का समाकलन गुणांक (I.F.)
का समाकलन गुणांक (I.F.) ![]() है।
है।
(v) ![]()
![]() अवकल समीकरण है।
अवकल समीकरण है।
(vi) यदि ![]() हो तो
हो तो ![]()
(vii) अवकल समी. ![]() की कोटि व घात
की कोटि व घात ![]() है।
है।
(viii) अवकल समी. ![]() का हल
का हल ![]() है।
है।
(ix) अवकल समी. ![]() का व्यापक हल
का व्यापक हल ![]() है।
है।
(x) अवकल समी. ![]() का हल
का हल ![]() है।
है।
प्रश्न क्रमांक 6:
1) सिद्ध करो कि ![]() अवकल समी.
अवकल समी. ![]() का हल है।
का हल है।
2) सिद्ध करो कि ![]() अवकल समी.
अवकल समी. ![]() का हल है।
का हल है।
3) ![]() का अवकल समी. ज्ञात करो जहाँ
का अवकल समी. ज्ञात करो जहाँ ![]() एक स्वेच्छ अचर है।
एक स्वेच्छ अचर है।
4) सिद्ध करो कि ![]() अवकल समी.
अवकल समी. ![]() का एक हल है।
का एक हल है।
5) अवकल समी. ![]() को हल कीजिये।
को हल कीजिये।
6) सिद्ध करो कि ![]() का एक व्यापक हल
का एक व्यापक हल ![]() है।
है।
7) ![]() का व्यापक हल ज्ञात करो।
का व्यापक हल ज्ञात करो।
8) सिद्ध करो कि ![]() का व्यापक हल
का व्यापक हल ![]() है।
है।
9) ![]() को हल कीजिये।
को हल कीजिये।
10) ![]() का समाकलन गुणांक ज्ञात करो।
का समाकलन गुणांक ज्ञात करो।
11) ![]() में
में ![]() और
और ![]() का मान ज्ञात करो।
का मान ज्ञात करो।
12) समघात समी. किसे कहते हैं? एक उदाहरण दीजिये।
13) रैखिक समी. क्या है? एक उदाहरण दीजिये।
14) रैखिक समी. ![]() का समाकलन गुणांक क्या होगा?
का समाकलन गुणांक क्या होगा?
15) अवकल समी. ![]() का व्यापक हल ज्ञात करो।
का व्यापक हल ज्ञात करो।
16) ![]() का व्यापक हल ज्ञात करो।
का व्यापक हल ज्ञात करो।
17) ![]() का व्यापक हल ज्ञात करो।
का व्यापक हल ज्ञात करो।
18) वक्रों के कुल ![]() जहाँ
जहाँ ![]() व
व ![]() स्वेच्छ अचर है को निरूपित करने वाले अवकल समी. को ज्ञात करो।
स्वेच्छ अचर है को निरूपित करने वाले अवकल समी. को ज्ञात करो।
19) ![]() की कोटि व घात बताओ।
की कोटि व घात बताओ।
20) ![]() का समाकलन गुणांक ज्ञात करो।
का समाकलन गुणांक ज्ञात करो।
21) ![]() का व्यापक हल ज्ञात करो।
का व्यापक हल ज्ञात करो।
22) ऐसे दीर्घवृत्तों के कुल का अवकल समी. ज्ञात करो जिनकी नाभियाँ ![]() -अक्ष पर है तथा जिनका केन्द्र मूल बिन्दु है।
-अक्ष पर है तथा जिनका केन्द्र मूल बिन्दु है।
23) ![]() का व्यापक हल ज्ञात करो।
का व्यापक हल ज्ञात करो।
24) ![]() का व्यापक हल ज्ञात करो।
का व्यापक हल ज्ञात करो।
25) ![]() ,
, ![]() का व्यापक हल ज्ञात करो।
का व्यापक हल ज्ञात करो।
26) ![]() का व्यापक हल ज्ञात करो।
का व्यापक हल ज्ञात करो।
27) अवकल समी. ![]() के लिए बिन्दु
के लिए बिन्दु ![]() से गुजरने वाला वक्र ज्ञात करो।
से गुजरने वाला वक्र ज्ञात करो।
28) ![]() का व्यापक हल ज्ञात करो।
का व्यापक हल ज्ञात करो।
29) ![]() का व्यापक हल ज्ञात करो।
का व्यापक हल ज्ञात करो।
30) ![]() , यदि
, यदि ![]() का विशिष्ट हल ज्ञात करो।
का विशिष्ट हल ज्ञात करो।
31) किसी बैंक में मूलधन की वृद्धि 5 प्रतिशत वार्षिक दर से होती है। इस बैंक में 1000 जमा कराए जाते हैं, ज्ञात कीजिए कि 10 वर्ष बाद यह राशि कितनी हो जाएगी? ![]()
32) अवकल समीकरण ![]() का व्यापक हल ज्ञात कीजिए।
का व्यापक हल ज्ञात कीजिए।
33) दर्शाइये कि समी. ![]() एक समघातीय समी. है। इसका व्यापक हल ज्ञात करो।
एक समघातीय समी. है। इसका व्यापक हल ज्ञात करो।
34) ![]() को हल करो।
को हल करो।
35) ![]() को हल करो।
को हल करो।
36) ![]() , यदि
, यदि ![]() जब
जब ![]() का विशिष्ट हल ज्ञात करो।
का विशिष्ट हल ज्ञात करो।
37) ![]() को हल कीजिये।
को हल कीजिये।
38) ![]() को हल कीजिये।
को हल कीजिये।
339) ![]() को हल करो।
को हल करो।
40) ![]() ;
; ![]() यदि
यदि ![]() का हल ज्ञात करो।
का हल ज्ञात करो।
41) ![]() का विशिष्ट हल ज्ञात करो।
का विशिष्ट हल ज्ञात करो। ![]() यदि
यदि ![]() हो।
हो।
42) ![]() ,
, ![]() को हल कीजिये।
को हल कीजिये।
43) अवकल समीकरण ![]() के लिए बिन्दु
के लिए बिन्दु ![]() से गुजरने वाला वक्र ज्ञात कीजिए।
से गुजरने वाला वक्र ज्ञात कीजिए।
प्रश्न-7 निम्नलिखित अवकल समीकरणों के व्यापक हल ज्ञात कीजिए।
(i) ![]()
(ii) ![]()
(iii) ![]()
(iv) ![]()
(v) ![]()
(vi) ![]()
(vii) ![]()
(viii) ![]()
(ix) ![]()
प्रश्न-8 निम्नलिखित अवकल समीकरणों के विशिष्ट हल ज्ञात कीजिए।
(i) ![]() ;
; ![]() यदि
यदि ![]()
(ii) ![]() ;
; ![]() यदि
यदि ![]()
(iii) ![]() ;
; ![]() यदि
यदि ![]()
(iv) ![]() ;
; ![]() यदि
यदि ![]()
उत्तर (अध्याय-9)
प्रश्न 1.
(i) a
(ii) b
(iii) c
(iv) d
(v) a
(vi) a
(vii) a
(viii) c
(ix) b
(x) d
(xi) a
(xii) d
(xiii) d
(xiv) a
प्रश्न 2.
(i) ![]()
(ii) ![]()
(iii) ![]()
(iv) 1, 2
(v) 2, 2
(vi) ![]()
(vii) ![]()
(viii) ![]()
(ix) ![]()
(x) ![]()
(xi) ![]()
(xii) ![]()
(xiii) 1, 6
(xiv) ![]()
प्रश्न 3.
(i) ब
(ii) अ
(iii) द
(iv) स
(v) फ
(vi) ड़
(vii) र
(viii) ल
प्रश्न 4.
(i) सत्य
(ii) असत्य
(iii) सत्य
(iv) असत्य
(v) सत्य
(vi) सत्य
(vii) सत्य
(viii) असत्य
(ix) सत्य
(x) सत्य
(xi) असत्य
(xii) असत्य
(xiii) सत्य
(xiv) सत्य