MP Board 12th Mathematics Continuity and Differentiability Question Bank : कक्षा 12 गणित अध्याय-5 : सातत्य एवं अवकलनीयता प्रश्न बैंक
अध्याय-5 सातत्य एवं अवकलनीयता
स्मरणीय बिंदु :
- एक वास्तविक माननीय फलन अपने प्रांत के किसी बिंदु पर संतत होता है यदि उस बिंदु पर फलन की सीमा, उस बिंदु पर फलन के मान के बराबर होती है।
- संतत फलनों के योग, अंतर, गुणनफल और भागफल संतत होते हैं, अर्थात्, यदि
 तथा
तथा 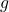 संतत फलन हैं, तो
संतत फलन हैं, तो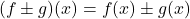 संतत होता है।
संतत होता है।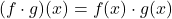 संतत होता है।
संतत होता है।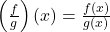 जहाँ
जहाँ 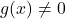 , संतत होता है।
, संतत होता है। - प्रत्येक अवकलनीय फलन संतत होता है किंतु इसका विलोम सत्य नहीं है।
- श्रृंखला-नियम फलनों के संयोजन का अवकलन करने के लिए एक नियम है। यदि
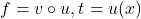 और यदि
और यदि 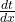 तथा
तथा 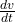 का अस्तित्व है तो
का अस्तित्व है तो 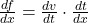
- कुछ मानक अवकलज (परिभाषित प्रांतों में) निम्नलिखित हैं :
- लघुगणकीय अवकलन,
![Rendered by QuickLaTeX.com f(x) = [u(x)]^{v(x)}](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-85a29b14e1202c5794f45554f4d7652b_l3.png) के रूप के फलनों के अवकलन करने के लिए एक सशक्त तकनीक है। इस तकनीक के अर्थपूर्ण होने के लिए आवश्यक है कि
के रूप के फलनों के अवकलन करने के लिए एक सशक्त तकनीक है। इस तकनीक के अर्थपूर्ण होने के लिए आवश्यक है कि  तथा
तथा 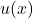 दोनों ही धनात्मक हों।
दोनों ही धनात्मक हों।
प्रश्न 1. सही विकल्प चुनिए-
(i) ![]() का
का ![]() के सापेक्ष अवकल गुणांक होगा।
के सापेक्ष अवकल गुणांक होगा।
(a) ![]()
(b) ![]()
(c) ![]()
(d) ![]()
(ii) ![]() का
का ![]() के सापेक्ष अवकल गुणांक होगा:
के सापेक्ष अवकल गुणांक होगा:
(a) ![]()
(b) ![]()
(c) ![]()
(d) ![]()
(iii) यदि ![]() , तब
, तब ![]() का मान होगा:
का मान होगा:
(a) ![]()
(b) ![]()
(c) ![]()
(d) इनमें से कोई नहीं
(iv) यदि ![]() तब
तब ![]()
(a) ![]()
(b) ![]()
(c) ![]()
(d) ![]()
(v) ![]() का
का ![]() के सापेक्ष अवकल गुणांक
के सापेक्ष अवकल गुणांक
(a) ![]()
(b) ![]()
(c) ![]()
(d) इनमें से कोई नहीं
प्रश्न 2. रिक्त स्थानों की पूर्ति कीजिए
(i) ![]() का
का ![]() के सापेक्ष अवकलन———–होगा।
के सापेक्ष अवकलन———–होगा।
(ii) ![]() का मान ———– होगा यदि
का मान ———– होगा यदि ![]()
(iii) ![]() तब
तब ![]() का मान———-होगा।
का मान———-होगा।
(iv) ![]() का
का ![]() के सापेक्ष अवकलन———है।
के सापेक्ष अवकलन———है।
(v) यदि ![]() है तो
है तो ![]() का मान———-है।
का मान———-है।
(vi) यदि ![]() तब
तब ![]() ………………
………………
(vii) यदि ![]() ………. तब
………. तब ![]() ………………
………………
(viii) यदि ![]() हो तो
हो तो ![]() का मान होगा………………
का मान होगा………………
(ix) यदि ![]() हो तो
हो तो ![]() के सापेक्ष अवकल का मान………………होगा
के सापेक्ष अवकल का मान………………होगा
(x) ![]() का अवकल गुणांक,……………… होता है
का अवकल गुणांक,……………… होता है
प्रश्न 3. सत्य/असत्य लिखिए –
(i) प्रत्येक बहुपद फलन सतत् होता है।
(ii) फलन ![]() ,
, ![]() पर सतत् व अवकलनीय है।
पर सतत् व अवकलनीय है।
(iii) प्रत्येक अवकलनीय फलन सतत् होता है।
(iv) ![]() का अवकल गुणांक
का अवकल गुणांक ![]() होता है।
होता है।
(v) यदि ![]() हो तो
हो तो ![]() का मान 1 होगा।
का मान 1 होगा।
(vi) ![]() का अवकल गुणांक
का अवकल गुणांक ![]() होगा
होगा
(vii) ![]() का अवकल गुणांक
का अवकल गुणांक ![]() होता है
होता है
(viii) ![]() का मान
का मान ![]() है
है
(ix) ![]() का अवकलन गुणांक
का अवकलन गुणांक ![]() होता हैं
होता हैं
(x) ![]() का अवकल गुणांक है
का अवकल गुणांक है ![]()
(xi) यदि ![]() हो तो
हो तो ![]()
(xii) किसी अचर राशि का अवकल गुणांक सदैव एक अचर होगा
प्रश्न 4. सही जोड़ी बनाइए
| खण्ड (अ) | खण्ड (ब) |
|---|---|
| (i) | (a). |
| (ii) | (b). सतत् होता है। |
| (iii) | (c). |
| (iv) | (d). |
| (v) प्रत्येक अवकलनीय फलन | (e). |
| (vi) | (f) |
| (vii) | (g) |
प्रश्न 5. एक शब्द/वाक्य में उत्तर दीजिए।
(i) यदि ![]() तब
तब ![]() क्या होगा?
क्या होगा?
(ii) ![]() का अवकलज लिखिए।
का अवकलज लिखिए।
(iii) यदि ![]() तो
तो ![]() का मान क्या होगा ?
का मान क्या होगा ?
(iv) यदि ![]() तब
तब ![]() का मान
का मान ![]() पर क्या होगा ?
पर क्या होगा ?
(v) ![]() का अवकल गुणांक क्या होगा
का अवकल गुणांक क्या होगा
(vi) ![]() का अवकल गुणांक क्या होगा
का अवकल गुणांक क्या होगा
(vii) ![]() का अवकल गुणांक क्या होगा
का अवकल गुणांक क्या होगा
(viii) ![]() का अवकल गुणांक क्या होगा
का अवकल गुणांक क्या होगा
(ix) ![]() का अवकल गुणांक क्या होगा
का अवकल गुणांक क्या होगा
प्रश्न क्रमांक 6
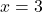 पर फलन
पर फलन 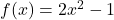 के सातत्य की जाँच कीजिए
के सातत्य की जाँच कीजिए- फलन
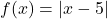 सतत है कि नही जांच कीजिए
सतत है कि नही जांच कीजिए - फलन
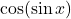 को
को  के सापेक्ष अवकलित कीजिए
के सापेक्ष अवकलित कीजिए 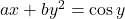 का
का 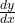 ज्ञात कीजिए
ज्ञात कीजिए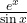 को
को  के सापेक्ष अवकलित कीजिए
के सापेक्ष अवकलित कीजिए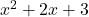 फलन का द्वितीय कोटि का अवकलज ज्ञात कीजिए
फलन का द्वितीय कोटि का अवकलज ज्ञात कीजिए- यदि
 सतत हो तो
सतत हो तो 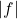 भी सतत होगा क्यों?
भी सतत होगा क्यों? - फलन
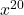 का द्वितीय कोटि का अवकलज ज्ञात कीजिए
का द्वितीय कोटि का अवकलज ज्ञात कीजिए - फलन
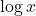 का द्वितीय कोटि का अवकलज ज्ञात कीजिए
का द्वितीय कोटि का अवकलज ज्ञात कीजिए 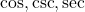 , और
, और 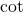 फलनों के विचार कीजिए कि कोन सतत है या असतत
फलनों के विचार कीजिए कि कोन सतत है या असतत- दर्शाए कि
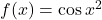 द्वारा परिभाषित फलन एक सतत फलन है ?
द्वारा परिभाषित फलन एक सतत फलन है ? - जाँच कीजिए कि क्या
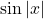 एक सतत फलन है ?
एक सतत फलन है ? 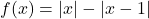 द्वारा परिभाषित है । फलन के सभी असतत के बिंदु को ज्ञात कीजिए
द्वारा परिभाषित है । फलन के सभी असतत के बिंदु को ज्ञात कीजिए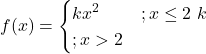 द्वारा परिभाषित फलन
द्वारा परिभाषित फलन 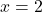 पर सतत है |
पर सतत है |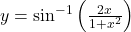 का
का 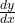 ज्ञात कीजिए |
ज्ञात कीजिए |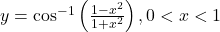 का
का 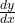 ज्ञात कीजिए |
ज्ञात कीजिए |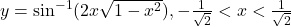 का
का 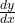 ज्ञात कीजिए |
ज्ञात कीजिए |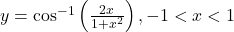 का
का 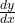 ज्ञात कीजिए |
ज्ञात कीजिए |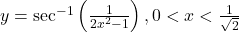 का
का 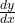 ज्ञात कीजिए |
ज्ञात कीजिए |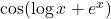 का
का 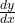 क्या होगा |
क्या होगा |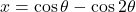 तथा
तथा 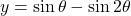 तब
तब 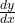 ज्ञात कीजिए |
ज्ञात कीजिए |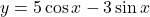 है तो सिद्ध कीजिए कि
है तो सिद्ध कीजिए कि 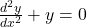
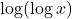 का
का 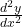 ज्ञात कीजिए |
ज्ञात कीजिए |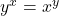 तब
तब 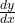 का मान क्या होगा |
का मान क्या होगा |- क्या फलन
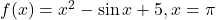 सतत है |
सतत है | - फलन
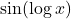 का द्वितीय कोटि के अवकलज ज्ञात कीजिए |
का द्वितीय कोटि के अवकलज ज्ञात कीजिए | - यदि
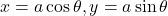 है तो
है तो 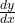 ज्ञात कीजिए |
ज्ञात कीजिए | - यदि
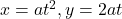 है तो
है तो 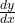 ज्ञात कीजिए |
ज्ञात कीजिए | 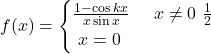 ,
, 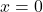 पर सतत है तो
पर सतत है तो  का मान ज्ञात कीजिए |
का मान ज्ञात कीजिए |- यदि
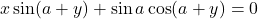 हो तो सिद्ध कीजिए :
हो तो सिद्ध कीजिए : 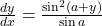
 का मान ज्ञात कीजिए यदि फलन
का मान ज्ञात कीजिए यदि फलन 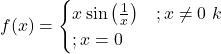 ,
, 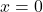 पर सतत है।
पर सतत है।- यदि
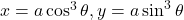 तो
तो 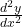 का मान
का मान 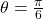 पर ज्ञात कीजिए।
पर ज्ञात कीजिए। 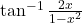 का
का 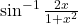 के सापेक्ष अवकलन कीजिए।
के सापेक्ष अवकलन कीजिए।- यदि
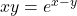 तो
तो 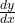 का मान ज्ञात कीजिए।
का मान ज्ञात कीजिए। - यदि
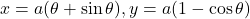 है तो
है तो 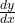 ज्ञात कीजिए।
ज्ञात कीजिए। - यदि
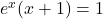 है तो दर्शाइए कि
है तो दर्शाइए कि 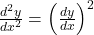
- यदि
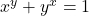 है तो
है तो 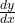 ज्ञात कीजिए।
ज्ञात कीजिए। - यदि
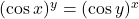 है तो
है तो 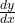 ज्ञात कीजिए।
ज्ञात कीजिए। - यदि
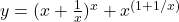 तो
तो 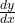 का मान ज्ञात कीजिए।
का मान ज्ञात कीजिए। - यदि
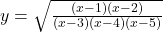 तो
तो 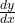 ज्ञात कीजिए।
ज्ञात कीजिए। - यदि
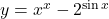 तो
तो 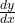 का मान ज्ञात कीजिए।
का मान ज्ञात कीजिए। - फलन
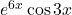 का द्वितीय कोटि के अवकलज ज्ञात कीजिए
का द्वितीय कोटि के अवकलज ज्ञात कीजिए - फलन
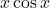 का द्वितीय कोटि के अवकलज ज्ञात कीजिए
का द्वितीय कोटि के अवकलज ज्ञात कीजिए - फलन
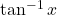 का द्वितीय कोटि के अवकलज ज्ञात कीजिए
का द्वितीय कोटि के अवकलज ज्ञात कीजिए - फलन
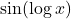 का द्वितीय कोटि के अवकलज ज्ञात कीजिए
का द्वितीय कोटि के अवकलज ज्ञात कीजिए
उत्तर- (अध्याय 5)
प्रश्न 1. (i) a (ii) c (iii) b (iv) b (v) a
प्रश्न 2. (i) ![]() (ii)
(ii) ![]() (iii)
(iii) ![]() (iv)
(iv) ![]() (v)
(v) ![]() (vi) 1 (vii)
(vi) 1 (vii) ![]() (viii)
(viii) ![]() (ix)
(ix) ![]() (x)
(x) ![]()
प्रश्न 3. (i) सत्य (ii) असत्य (iii) सत्य (iv) असत्य (v) असत्य (vi) असत्य (vii) सत्य (viii) असत्य (ix) सत्य (x) सत्य (xi) सत्य (xii) असत्य
प्रश्न 4. (i) f (ii) d (iii) e (iv) c (v) b (vi) g (vii) a
प्रश्न 5. (i) ![]() (ii)
(ii) ![]() (iii) 2 (iv)
(iii) 2 (iv) ![]() (v)
(v) ![]() (vi)
(vi) ![]() (vii)
(vii) ![]() (viii)
(viii) ![]() (ix)
(ix) ![]()