MP Board 10th Mathematics One Liner part 2 : MP Board 10th Mathematics One Liner Part 2 विद्यार्थियों को बोर्ड परीक्षा की तैयारी में महत्वपूर्ण सहयोग प्रदान करता है। इस भाग में गणित के मुख्य अध्यायों जैसे निर्देशांक ज्यामिति (Coordinate Geometry), त्रिकोणमिति का परिचय (Introduction to Trigonometry), त्रिकोणमिति के कुछ अनुप्रयोग (Some Applications of Trigonometry), वृत्त (Circles) और रचनाएँ (Constructions) से संबंधित महत्वपूर्ण प्रश्न शामिल किए गए हैं।
MP Board 10th Mathematics One Liner Part 2 के माध्यम से विद्यार्थी आसानी से कठिन प्रश्नों की पुनरावृत्ति कर सकते हैं। निर्देशांक ज्यामिति में दूरी सूत्र, विभाजन सूत्र और क्षेत्रफल से संबंधित प्रश्न आते हैं। त्रिकोणमिति के परिचय में पहचान सूत्र और कोणों के मान महत्वपूर्ण हैं, वहीं त्रिकोणमिति के अनुप्रयोग अध्याय में ऊँचाई और दूरी पर आधारित प्रश्न बार-बार पूछे जाते हैं। वृत्त (Circles) अध्याय में स्पर्शरेखा और ज्यामितीय गुणों पर प्रश्न पूछे जाते हैं। रचनाएँ (Constructions) में त्रिभुज और अन्य आकृतियों की ज्यामितीय रचना के प्रश्न महत्वपूर्ण रहते हैं।
इस प्रकार MP Board 10th Mathematics One Liner Part 2 विद्यार्थियों के लिए एक सरल, सटीक और प्रभावी अध्ययन सामग्री है जो परीक्षा में अच्छे अंक प्राप्त करने में मददगार होगी।
| MP Board 10th Mathematics One Liner part 1 MP Board 10th Mathematics One Liner part 2 MP Board 10th Mathematics One Liner part 3 |
- वास्तविक संख्याएँ (Real Numbers)
- बहुपद (Polynomials)
- दो चर वाले रैखिक समीकरणों का युग्म (Pair of Linear Equations in Two Variables)
- द्विघात समीकरण (Quadratic Equations)
- समांतर श्रेढ़ियाँ (Arithmetic Progressions)
- त्रिभुज (Triangles)
- निर्देशांक ज्यामिति (Coordinate Geometry)
- त्रिकोणमिति का परिचय (Introduction to Trigonometry)
- त्रिकोणमिति के कुछ अनुप्रयोग (Some Applications of Trigonometry)
- वृत्त (Circles)
- रचनाएँ (Constructions)
- वृत्तों से संबंधित क्षेत्रफल (Areas Related to Circles)
- पृष्ठीय क्षेत्रफल और आयतन (Surface Areas and Volumes)
- सांख्यिकी (Statistics)
- प्रायिकता (Probability)
MP Board 10th Mathematics One Liner part 2
अध्याय – 7
निर्देशांक ज्यामिति
- किसी बिंदु की
 -अक्ष से दूरी, उस बिंदु का
-अक्ष से दूरी, उस बिंदु का  -निर्देशांक (भुज) होता है।
-निर्देशांक (भुज) होता है।
उदाहरण : बिंदु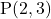 की
की  -अक्ष से दूरी 2 है।
-अक्ष से दूरी 2 है। - किसी बिंदु की
 -अक्ष से दूरी, उस बिंदु का
-अक्ष से दूरी, उस बिंदु का  -निर्देशांक (कोटि) होता है।
-निर्देशांक (कोटि) होता है।
उदाहरण : बिंदु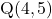 की
की  -अक्ष से दूरी 5 है।
-अक्ष से दूरी 5 है।  -अक्ष पर स्थित किसी बिंदु के निर्देशांक
-अक्ष पर स्थित किसी बिंदु के निर्देशांक 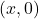 के रूप में होते हैं तथा
के रूप में होते हैं तथा  -अक्ष पर स्थित किसी बिंदु के निर्देशांक
-अक्ष पर स्थित किसी बिंदु के निर्देशांक 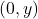 के रूप में होते हैं।
के रूप में होते हैं।- बिंदुओं
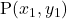 और
और 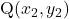 के बीच की दूरी
के बीच की दूरी 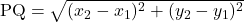 होती है।
होती है।
उदाहरण:
बिंदुओं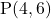 और
और 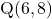 के बीच की दूरी ज्ञात करना।
के बीच की दूरी ज्ञात करना।
यहाँ पर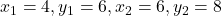 ,
,
अतः दोनों बिंदुओं के बीच की दूरी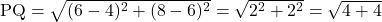
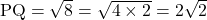 मात्रक
मात्रक - बिंदु
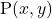 की मूल बिंदु
की मूल बिंदु 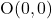 से दूरी
से दूरी 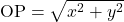 होती है।
होती है।
उदाहरण : बिंदु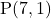 और मूल बिंदु
और मूल बिंदु 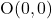 से दूरी
से दूरी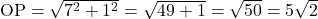
- दो बिंदुओं
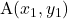 और
और 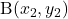 को जोड़ने वाले रेखाखंड
को जोड़ने वाले रेखाखंड 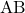 को
को 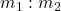 के अनुपात में आंतरिक रूप से विभाजित करने वाले बिंदु
के अनुपात में आंतरिक रूप से विभाजित करने वाले बिंदु 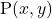 के निर्देशांक हैं –
के निर्देशांक हैं –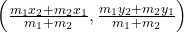
- बिंदुओं
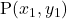 और
और 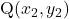 को जोड़ने वाले रेखाखंड
को जोड़ने वाले रेखाखंड 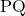 के मध्य बिंदु के निर्देशांक
के मध्य बिंदु के निर्देशांक 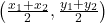 होते हैं।
होते हैं।
उदाहरण :
बिंदुओं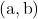 और
और 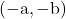 का मध्य बिंदु ज्ञात करना।
का मध्य बिंदु ज्ञात करना।
हल : यदि मध्य बिंदु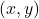 हैं, तो
हैं, तो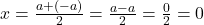
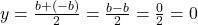
अतः मध्य बिंदु के निर्देशांक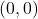 हैं।
हैं।
अध्याय- 8
त्रिकोणमिति का परिचय
अवधारणाओं पर आधारित महत्वपूर्ण तथ्य
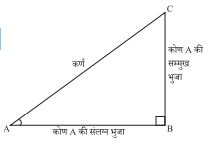
- समकोण त्रिभुज ABC के कोण A के त्रिकोणमितीय अनुपात निम्न प्रकार से परिभाषित किये जाते हैं
- सुविधा के लिए
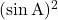 के स्थान पर हम
के स्थान पर हम 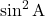 लिख सकते हैं। परंतु
लिख सकते हैं। परंतु 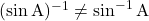
- समकोण त्रिभुज का कर्ण, त्रिभुज की सबसे लंबी भुजा होती है, इसलिए
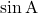 या
या 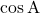 का मान सदा
का मान सदा 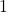 से कम होता है। (या विशेष स्थिति में 1 के बराबर होता है)
से कम होता है। (या विशेष स्थिति में 1 के बराबर होता है) 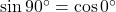
- इसी प्रकार
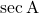 और
और 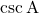 का मान सदैव
का मान सदैव 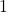 से अधिक या
से अधिक या 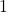 के बराबर होता है।
के बराबर होता है। 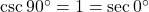
- समकोण त्रिभुज के किसी न्यूनकोण
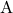 में वृद्धि होने के साथ
में वृद्धि होने के साथ 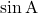 के मान में भी वृद्धि होती है।
के मान में भी वृद्धि होती है। 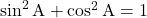 एक त्रिकोणमितीय सर्वसमिका है, जहाँ
एक त्रिकोणमितीय सर्वसमिका है, जहाँ 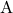 किसी समकोण त्रिभुज का एक न्यूनकोण है।
किसी समकोण त्रिभुज का एक न्यूनकोण है।- उपरोक्त सर्वसमिका से दो अन्य सर्वसमिकाएँ
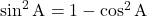 तथा
तथा 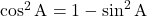 प्राप्त होती हैं।
प्राप्त होती हैं। - अन्य त्रिकोणमितीय सर्वसमिकाएँ हैं,
i)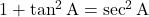 , जहाँ
, जहाँ 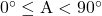
ii)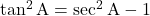 , जहाँ
, जहाँ 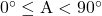
iii)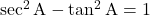 , जहाँ
, जहाँ 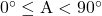
iv)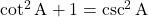 , जहाँ
, जहाँ 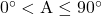
v)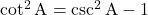 , जहाँ
, जहाँ 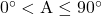
vi)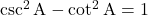 , जहाँ
, जहाँ 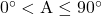
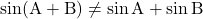
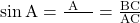
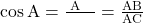
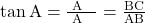
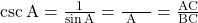
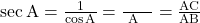
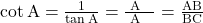
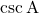 व्युत्क्रम है
व्युत्क्रम है 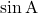 का अर्थात
का अर्थात 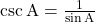
- इसी प्रकार
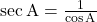 तथा
तथा 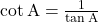
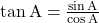 तथा
तथा 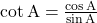
अध्याय- 9
त्रिकोणमिति के कुछ अनुप्रयोग
अवधारणाओं पर आधारित महत्वपूर्ण तथ्य
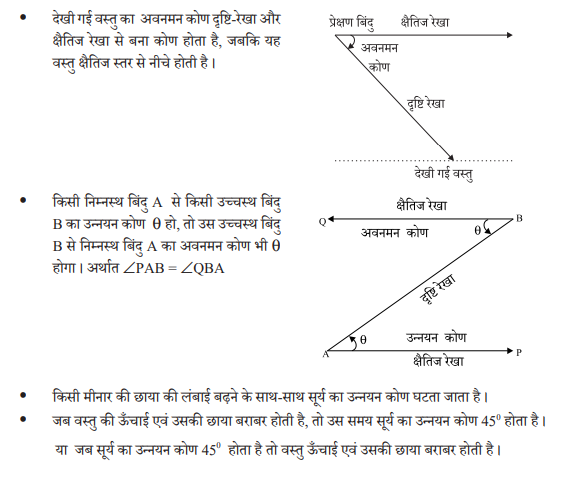
वह रेखा जो हमारी आँख से सीधे भूमि के समान्तर जाती है, क्षैतिज रेखा कहलाती है।
हमारी आँख (प्रेक्षण बिंदु) से उस वस्तु को जिसे हम देख रहे हैं, जोड़ने वाली रेखा उस वस्तु की दृष्टि रेखा कहलाती है।
उन्नयन कोण उस स्थिति में बनता है जबकि वस्तु को देखने के लिये हमें अपने सिर को ऊपर उठाना होता है, अर्थात नीचे से ऊपर की ओर देखने पर।
देखी गई वस्तु का उन्नयन कोण दृष्टि-रेखा और क्षैतिज रेखा से बना कोण होता है जबकि यह वस्तु क्षैतिज स्तर से ऊपर होती है।
दखी गई वस्तु का उन्स्यन कोण दृष्टि-रेखा और क्षैतिज रेखा से बना कोण होता है जबकि यह वस्तु क्षैतिज स्तर से ऊपर होती है ।
2 thoughts on “MP Board 10th Mathematics One Liner part 2”