MP Board 10th Mathematics One Liner part 1 : MP Board 10th Mathematics One Liner विद्यार्थियों के लिए बेहद उपयोगी सामग्री है। इस MP Board 10th Mathematics One Liner part 1 में गणित के मुख्य अध्यायों जैसे वास्तविक संख्याएँ (Real Numbers), बहुपद (Polynomials), दो चर वाले रैखिक समीकरणों का युग्म (Pair of Linear Equations in Two Variables), द्विघात समीकरण (Quadratic Equations) तथा समांतर श्रेढ़ियाँ (Arithmetic Progressions) से संबंधित महत्वपूर्ण प्रश्न शामिल किए गए हैं। MP Board 10th Mathematics One Liner part 1 विद्यार्थियों को परीक्षा की बेहतर तैयारी में सहायता करते हैं। इन प्रश्नों के माध्यम से विद्यार्थी कठिन अध्यायों की पुनरावृत्ति आसानी से कर सकते हैं और कम समय में अधिक अभ्यास कर सकते हैं। MP Board 10th Mathematics One Liner Most Imp Questions उन छात्रों के लिए विशेष रूप से लाभदायक हैं जो बोर्ड परीक्षा में अच्छे अंक प्राप्त करना चाहते हैं। यह संग्रह सरल भाषा और सटीक प्रश्नों के माध्यम से विद्यार्थियों को आत्मविश्वास प्रदान करता है।

MP Board 10th Mathematics One Liner part 1
- वास्तविक संख्याएँ (Real Numbers)
- बहुपद (Polynomials)
- दो चर वाले रैखिक समीकरणों का युग्म (Pair of Linear Equations in Two Variables)
- द्विघात समीकरण (Quadratic Equations)
- समांतर श्रेढ़ियाँ (Arithmetic Progressions)
- त्रिभुज (Triangles)
MP Board 10th Mathematics One Liner part 2
- निर्देशांक ज्यामिति (Coordinate Geometry)
- त्रिकोणमिति का परिचय (Introduction to Trigonometry)
- त्रिकोणमिति के कुछ अनुप्रयोग (Some Applications of Trigonometry)
- वृत्त (Circles)
- रचनाएँ (Constructions)
MP Board 10th Mathematics One Liner part 3
- वृत्तों से संबंधित क्षेत्रफल (Areas Related to Circles)
- पृष्ठीय क्षेत्रफल और आयतन (Surface Areas and Volumes)
- सांख्यिकी (Statistics)
- प्रायिकता (Probability)
MP Board 10th Mathematics One Liner part 1
अध्याय – 1
वास्तविक संख्याएँ
अवधारणाओं पर आधारित महत्वपूर्ण तथ्य
- प्रत्येक भाज्य संख्या को एक अद्वितीय रूप से अभाज्य संख्याओं के गुणनफल के रूप में व्यक्त किया जा सकता है। यही अंकगणित की आधारभूत प्रमेय है।
- किसी भी प्राकृत संख्या को उसके अभाज्य गुणनखंडों के एक गुणनफल के रूप में लिखा जा सकता है।
उदाहरणार्थ,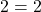 ,
, 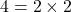 ,
, 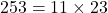
- “एक प्राकृत संख्या का अभाज्य गुणनखंड उसके गुणनखंडों के क्रम को छोड़ते हुए अद्वितीय होता है।”
- कार्ल फ्रेडरिक गॉस को ‘गणितज्ञों का राजकुमार’ कहा जाता है।
- “संख्याओं में प्रत्येक उभयनिष्ठ अभाज्य गुणनखंड की सबसे छोटी घात का गुणनफल महत्तम समापवर्तक (HCF) कहलाता है।” उदाहरणार्थ –
12, 15 और 21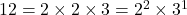
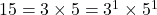
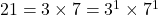
महत्तम समापवर्तक (HCF)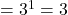
- “संख्याओं में संबद्ध प्रत्येक अभाज्य गुणनखंड की सबसे बड़ी घात का गुणनफल लघुत्तम समापवर्त्य (LCM) कहलाता है।” उदाहरणार्थ –
6, 20 और 21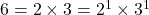
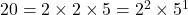
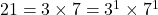
लघुत्तम समापवर्त्य (LCM)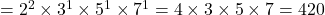
- किसी प्राकृत संख्या
 के लिए, संख्या
के लिए, संख्या 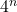 अंक 0 (शून्य) पर समाप्त नहीं होगी क्योंकि 0 (शून्य) पर समाप्त होने वाली संख्याएँ 5 से विभाज्य होती हैं और ये संख्याएँ 5 से विभाज्य नहीं हैं।
अंक 0 (शून्य) पर समाप्त नहीं होगी क्योंकि 0 (शून्य) पर समाप्त होने वाली संख्याएँ 5 से विभाज्य होती हैं और ये संख्याएँ 5 से विभाज्य नहीं हैं। - किन्हीं दो धनात्मक पूर्णांकों
 और
और  के लिए, HCF
के लिए, HCF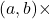 LCM
LCM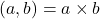 होता है।
होता है। - दो संख्याओं का गुणनफल, उनके HCF और LCM के गुणनफल के बराबर होता है, परन्तु तीन संख्याओं का गुणनफल उनके HCF और LCM के गुणनफल के बराबर नहीं होता है।
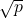 अपरिमेय संख्या है, जहाँ
अपरिमेय संख्या है, जहाँ  एक अभाज्य संख्या है।
एक अभाज्य संख्या है। 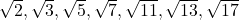 इत्यादि अपरिमेय संख्याएँ हैं।
इत्यादि अपरिमेय संख्याएँ हैं।- यदि
 कोई अभाज्य संख्या है और
कोई अभाज्य संख्या है और  ,
, 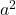 को विभाजित करता है तो
को विभाजित करता है तो  ,
,  को भी विभाजित करेगा, जहाँ
को भी विभाजित करेगा, जहाँ  एक धनात्मक पूर्णांक है।
एक धनात्मक पूर्णांक है। - एक परिमेय संख्या और एक अपरिमेय संख्या का योग या अंतर एक अपरिमेय संख्या होती है। उदाहरणार्थ:
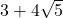 ,
, 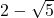 .
. - एक शून्येतर परिमेय संख्या और एक अपरिमेय संख्या का गुणनफल या भागफल एक अपरिमेय संख्या होती है।
- एक परिमेय संख्या और एक अपरिमेय संख्या का योग या अंतर एक अपरिमेय संख्या होती है। उदाहरणार्थ:
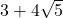 ,
, 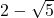
- एक शून्येतर परिमेय संख्या और एक अपरिमेय संख्या का गुणनफल या भागफल एक अपरिमेय संख्या होती है।
अध्याय – 2
बहुपद
- चर
 के बहुपद
के बहुपद 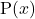 में
में  की उच्चतम घात बहुपद की घात कहलाती है।
की उच्चतम घात बहुपद की घात कहलाती है।
बहुपद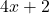 चर
चर  में घात 1 का बहुपद है, क्योंकि चर
में घात 1 का बहुपद है, क्योंकि चर  की अधिकतम घात 1 है।
की अधिकतम घात 1 है।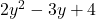 , चर
, चर  में घात 2 का बहुपद है क्योंकि चर
में घात 2 का बहुपद है क्योंकि चर  की अधिकतम घात 2 है।
की अधिकतम घात 2 है।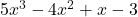 चर
चर  में घात 3 का बहुपद है, क्योंकि चर
में घात 3 का बहुपद है, क्योंकि चर  की उच्चतम घात 3 है।
की उच्चतम घात 3 है। - ऐसे बहुपद जिनकी घात 1 होती है रैखिक बहुपद कहलाते हैं। जैसे
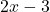 ,
, 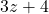 ,
, 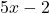 आदि में बहुपद की अधिकतम घात 1 है, अतः ये रैखिक बहुपद हैं।
आदि में बहुपद की अधिकतम घात 1 है, अतः ये रैखिक बहुपद हैं। 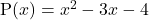 में
में 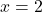 रखने पर
रखने पर 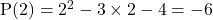 प्राप्त होता है यह
प्राप्त होता है यह 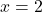 पर
पर 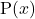 का मान है।
का मान है।- यदि बहुपद
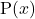 में
में  को किसी वास्तविक संख्या
को किसी वास्तविक संख्या  से प्रतिस्थापित करने पर बहुपद का मान शून्य प्राप्त होता है, अर्थात
से प्रतिस्थापित करने पर बहुपद का मान शून्य प्राप्त होता है, अर्थात 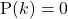 , तो
, तो  बहुपद का शून्यक कहलाता है।
बहुपद का शून्यक कहलाता है।
बहुपद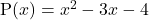 का
का 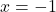 पर मान
पर मान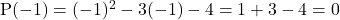
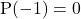 , अतः
, अतः 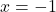 बहुपद
बहुपद 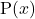 का शून्यक है।
का शून्यक है। - किसी बहुपद
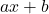 ;
; 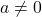 का शून्यक उस बिंदु का
का शून्यक उस बिंदु का  -निर्देशांक होता है, जहाँ
-निर्देशांक होता है, जहाँ 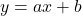 का ग्राफ
का ग्राफ  -अक्ष को प्रतिच्छेद करता है।
-अक्ष को प्रतिच्छेद करता है। - बहुपद
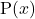 का ग्राफ
का ग्राफ  -अक्ष को जितने बिंदुओं पर प्रतिच्छेद करता है, उस बहुपद
-अक्ष को जितने बिंदुओं पर प्रतिच्छेद करता है, उस बहुपद 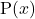 के उतने ही शून्यक होते हैं।
के उतने ही शून्यक होते हैं। - रेखीय बहुपद का व्यापक रूप
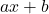 है, जहाँ
है, जहाँ  , चर
, चर  का गुणांक एवं
का गुणांक एवं  अचर पद है तथा
अचर पद है तथा 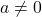 .
. - द्विघात बहुपद का व्यापक रूप
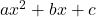 , जहाँ
, जहाँ 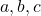 वास्तविक संख्याएँ हैं तथा
वास्तविक संख्याएँ हैं तथा 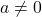 .
. 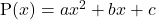 द्विघात बहुपद के शून्यक
द्विघात बहुपद के शून्यक  और
और  हैं तो
हैं तो
शून्यकों का योगफल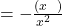
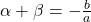
और शून्यकों का गुणनफल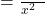
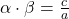
- बहुपद
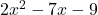 में शून्यकों का योगफल
में शून्यकों का योगफल 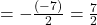 होगा।
होगा। 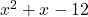 बहुपद में शून्यकों का गुणनफल
बहुपद में शून्यकों का गुणनफल 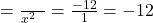 होगा।
होगा।- किसी
 घात के लिए दिए गए बहुपद
घात के लिए दिए गए बहुपद 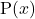 के लिए
के लिए 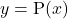 का ग्राफ
का ग्राफ  -अक्ष को अधिक से अधिक
-अक्ष को अधिक से अधिक  बिंदुओं पर प्रतिच्छेद करता है। अतः
बिंदुओं पर प्रतिच्छेद करता है। अतः  घात के किसी बहुपद के अधिक से अधिक
घात के किसी बहुपद के अधिक से अधिक  शून्यक हो सकते हैं।
शून्यक हो सकते हैं। - बहुपद
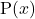 का ग्राफ
का ग्राफ  -अक्ष को 3 बिंदुओं पर प्रतिच्छेद कर रहा है अतः:
-अक्ष को 3 बिंदुओं पर प्रतिच्छेद कर रहा है अतः:
बहुपद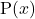 के तीन शून्यक होंगे।
के तीन शून्यक होंगे। - किसी द्विघात बहुपद
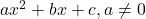 के संगत समीकरण
के संगत समीकरण 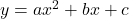 का ग्राफ परवलय होता है।
का ग्राफ परवलय होता है। - यदि
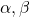 किसी द्विघात बहुपद के शून्यक हैं तो द्विघात बहुपद
किसी द्विघात बहुपद के शून्यक हैं तो द्विघात बहुपद ![Rendered by QuickLaTeX.com \text{P}(x) = k[x^2-(\alpha+\beta)x+\alpha\beta]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-d809ae064e7d3eb59ed09d5a2ea60285_l3.png) की तरह का होगा जहाँ
की तरह का होगा जहाँ  कोई वास्तविक संख्या है।
कोई वास्तविक संख्या है। - बहुपद के शून्यकों का योग
 व गुणनफल 2 है तो बहुपद
व गुणनफल 2 है तो बहुपद 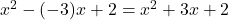 होगा।
होगा। - त्रिघात बहुपद
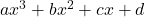 के शून्यक
के शून्यक 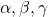 हों तो शून्यकों तथा गुणांकों में संबंध
हों तो शून्यकों तथा गुणांकों में संबंध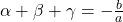
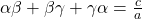
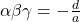
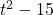 बहुपद में
बहुपद में 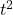 का गुणांक
का गुणांक 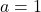 ,
,  का गुणांक
का गुणांक 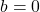 तथा अचर पद
तथा अचर पद 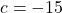 है, तब
है, तब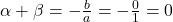
और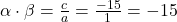
अध्याय – 3
दो चर वाले रैखिक समीकरण युग्म
- दो चर वाले रैखिक समीकरण को प्रदर्शित करने वाला मानक रूप:
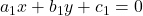 और
और 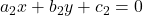 है, जहाँ
है, जहाँ  व
व  चर हैं और
चर हैं और 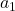 ,
, 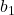 ,
, 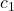 और
और 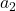 ,
, 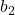 ,
, 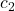 गुणांक हैं।
गुणांक हैं। - दो चर वाले रैखिक समीकरण युग्म का हल, एक ऐसा बिंदु होता है, जो कि युग्म की दोनों रेखाओं पर स्थित हो।
- रैखिक युग्म की रेखाएँ एक बिंदु पर प्रतिच्छेद करती हैं, तो इस स्थिति में, समीकरण युग्म का एक अद्वितीय हल होता है।
- एक रैखिक समीकरण युग्म, जिसका हल होता है, रैखिक समीकरणों का संगत (consistent) युग्म कहलाता है।
- रैखिक युग्म की रेखाएँ संपाती होती हैं, तो इस स्थिति में, समीकरण के अपरिमित रूप से अनेक हल होते हैं एवं इस युग्म को दो चरों के रैखिक समीकरणों का आश्रित (dependent) युग्म कहते हैं।
- रैखिक समीकरणों का आश्रित युग्म सदैव संगत (consistent) होता है।
- दो चर वाले रैखिक समीकरण युग्म की रेखाएँ समांतर होती हैं, तो इस स्थिति में, समीकरणों का कोई भी हल नहीं होता है।
- रैखिक समीकरण युग्म, जिसका कोई हल नहीं होता, रैखिक समीकरणों का असंगत (inconsistent) युग्म कहलाता है।
- रैखिक समीकरण युग्म:
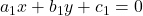 और
और 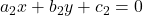 में निम्न स्थितियाँ उत्पन्न हो सकती हैं:
में निम्न स्थितियाँ उत्पन्न हो सकती हैं:
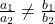 : इस स्थिति में, रैखिक समीकरण युग्म संगत होता है एवं समीकरणों का एक अद्वितीय हल होता है तथा रेखाएँ प्रतिच्छेदी होती हैं।
: इस स्थिति में, रैखिक समीकरण युग्म संगत होता है एवं समीकरणों का एक अद्वितीय हल होता है तथा रेखाएँ प्रतिच्छेदी होती हैं।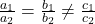 : इस स्थिति में, रैखिक समीकरण युग्म असंगत होता है एवं समीकरणों का कोई भी हल नहीं होता है तथा रेखाएँ समांतर होती हैं।
: इस स्थिति में, रैखिक समीकरण युग्म असंगत होता है एवं समीकरणों का कोई भी हल नहीं होता है तथा रेखाएँ समांतर होती हैं। : इस स्थिति में, रैखिक समीकरण युग्म आश्रित (संगत) होता है एवं समीकरणों के अनंत हल होते हैं तथा रेखाएँ संपाती होती हैं।
: इस स्थिति में, रैखिक समीकरण युग्म आश्रित (संगत) होता है एवं समीकरणों के अनंत हल होते हैं तथा रेखाएँ संपाती होती हैं।
- रैखिक समीकरण युग्म के ग्राफीय विधि द्वारा हल में दोनों समीकरणों को ग्राफ में प्रदर्शित कर उनके प्रतिच्छेद बिंदु के निर्देशांक ज्ञात करते हैं, जो कि समीकरण युग्म का हल होता है।
अध्याय – 4
द्विघात समीकरण
- जब हम द्विघात बहुपद को शून्य के तुल्य कर देते हैं तो हमें **द्विघात समीकरण** प्राप्त हो जाती है।
- यदि
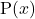 , घात दो का एक बहुपद है, तो समीकरण
, घात दो का एक बहुपद है, तो समीकरण 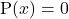 , एक **द्विघात समीकरण** कहलाता है।
, एक **द्विघात समीकरण** कहलाता है। 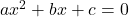 जहाँ
जहाँ 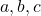 वास्तविक संख्याएँ हैं तथा
वास्तविक संख्याएँ हैं तथा  , **द्विघात समीकरण** का मानक रूप है।
, **द्विघात समीकरण** का मानक रूप है।- द्विघात समीकरण के कुछ उदाहरण :
(i)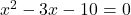
(ii)
(iii)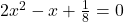 आदि
आदि - **द्विघात समीकरण का हल**
(i) **गुणनखंड विधि** :-
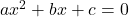 ,
, 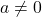 को दो रैखिक गुणनखंडों में गुणनखंड करके प्रत्येक गुणक को शून्य के बराबर करके हल प्राप्त करते हैं, तो द्विघात समीकरण
को दो रैखिक गुणनखंडों में गुणनखंड करके प्रत्येक गुणक को शून्य के बराबर करके हल प्राप्त करते हैं, तो द्विघात समीकरण 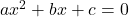 के मूल प्राप्त होते हैं।
के मूल प्राप्त होते हैं।
उदाहरण :-
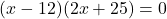
अतः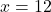 या
या 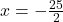
- **सूत्र विधि** :-
श्रीधराचार्य (सा. यु. 1025) द्वारा द्विघात समीकरण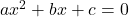 ,
, 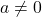 को हल करने के लिए सूत्र प्रतिपादित किया जिसे “द्विघात सूत्र” कहते हैं।
को हल करने के लिए सूत्र प्रतिपादित किया जिसे “द्विघात सूत्र” कहते हैं।
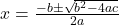
उदाहरण :- द्विघात समीकरण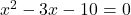 को द्विघात सूत्र द्वारा हल करना :-
को द्विघात सूत्र द्वारा हल करना :-
द्विघात समी. की मानक रूप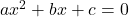 से तुलना करने पर
से तुलना करने पर 
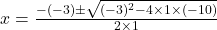
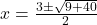
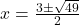
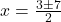
**+** चिन्ह लेने पर
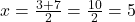
**-** चिन्ह लेने पर
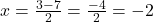
अतः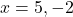
- द्विघात समीकरण का **विविक्तकर** (discriminant)
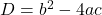 होता है, जहाँ
होता है, जहाँ  द्विघात समीकरण
द्विघात समीकरण 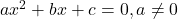 के क्रमश:
के क्रमश:  का गुणांक,
का गुणांक,  का गुणांक तथा अचर पद हैं।
का गुणांक तथा अचर पद हैं। - **द्विघात समीकरण के मूलों की प्रकृति** में द्विघात समीकरण
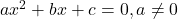 में
में
(i) दो भिन्न वास्तविक मूल होते हैं, यदि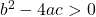 हो
हो
(ii) दो वास्तविक एवं बराबर मूल होते हैं यदि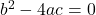 हो
हो
(iii) कोई वास्तविक मूल नहीं होते हैं यदि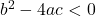 हो
हो
उदाहरण :- द्विघात समीकरण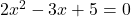 के मूलों की प्रकृति ज्ञात करना :-
के मूलों की प्रकृति ज्ञात करना :-
दी हुई समीकरण की तुलना मानक रूप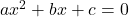 से करने पर
से करने पर 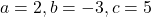
विविक्तकर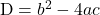
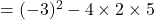
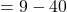
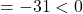
अतः द्विघात समी.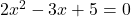 के कोई वास्तविक मूल नहीं होंगे।
के कोई वास्तविक मूल नहीं होंगे।
अध्याय- 5
समांतर श्रेणियाँ
- प्रकृति में अनेक वस्तुएँ एक निश्चित प्रतिरूप (pattern) का अनुसरण करती हैं जैसे कि सूरजमुखी के फूल की पंखुड़ियाँ, मधु-कोष (या मधु छत्ते) में छिद्र, एक भूट्टे पर दाने, एक अनन्नास और एक पाइन कोन पर सर्पिल इत्यादि।
- **दैनिक जीवन में निश्चित प्रतिरूप का उदाहरण** –
किसी व्यक्ति की प्रथम मासिक वेतन ₹8000 और ₹500 वार्षिक वेतन वृद्धि होने पर प्रथम, द्वितीय और तृतीय वर्ष इत्यादि के लिए वेतन 8000, 8500, 9000 ….. होगा।
**अन्य प्रतिरूप**
(i)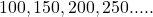
(ii)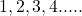
(iii)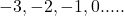
(iv)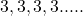
(v)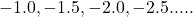
उपरोक्त सूची में उत्तरोत्तर पदों में एक निश्चित संख्या जोड़कर प्राप्त किया जाता है। संख्याओं की ऐसी सूची को **समांतर श्रेढ़ी** (Arithmetic Progression या A.P.) कहा जाता है। - एक समांतर श्रेढ़ी संख्याओं की ऐसी सूची होती है, जिसमें प्रत्येक पद (प्रथम पद के अतिरिक्त) अपने से ठीक पहले पद में एक निश्चित संख्या
 जोड़कर प्राप्त होता है। यह निश्चित संख्या
जोड़कर प्राप्त होता है। यह निश्चित संख्या  इस समांतर श्रेढ़ी का **सार्वअंतर** कहलाती है। सार्वअंतर धनात्मक, ऋणात्मक या शून्य हो सकता है।
इस समांतर श्रेढ़ी का **सार्वअंतर** कहलाती है। सार्वअंतर धनात्मक, ऋणात्मक या शून्य हो सकता है। - A.P. के प्रथम पद को
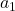 , दूसरे पद को
, दूसरे पद को 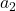 , ….. इसी प्रकार
, ….. इसी प्रकार  वें पद को
वें पद को  से दर्शाते हैं। A.P. को निम्नलिखित रूप में व्यक्त कर सकते हैं।
से दर्शाते हैं। A.P. को निम्नलिखित रूप में व्यक्त कर सकते हैं।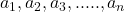
**समांतर श्रेढ़ी में हर अगले पद में से पिछले पद को घटाकर सार्वअंतर प्राप्त होता है**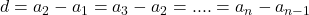
- समांतर श्रेढ़ी का व्यापक रूप (general form)
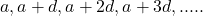
जहाँ पहला पद और
पहला पद और  सार्व अंतर है।
सार्व अंतर है। - समांतर श्रेढ़ी में पदों की संख्या परिमित होने पर श्रेढ़ी को **परिमित समांतर श्रेढ़ी** कहते हैं। परिमित समांतर श्रेढ़ी में **अंतिम पद** (last term) होता है।
उदाहरण :-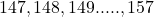
- **अपरिमित समांतर श्रेढ़ी** में पदों की संख्या अपरिमित होती है। इसमें अंतिम पद नहीं होता है।
उदाहरण: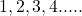
- प्रथम पद
 और सार्वअंतर
और सार्वअंतर  वाली एक समांतर श्रेढ़ी का
वाली एक समांतर श्रेढ़ी का  वाँ पद निम्नलिखित सूत्र से प्राप्त होता है –
वाँ पद निम्नलिखित सूत्र से प्राप्त होता है –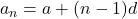
 को A.P. का **व्यापक पद** (general term) भी कहते हैं। यदि किसी A.P. में
को A.P. का **व्यापक पद** (general term) भी कहते हैं। यदि किसी A.P. में  पद हैं तो
पद हैं तो 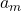 इसके अंतिम पद को निरूपित करता है। अंतिम पद को
इसके अंतिम पद को निरूपित करता है। अंतिम पद को  द्वारा भी निरूपित किया जाता है।
द्वारा भी निरूपित किया जाता है। - A.P.
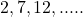 का 7 वाँ पद ज्ञात करना।
का 7 वाँ पद ज्ञात करना।
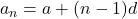
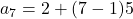
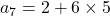
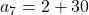
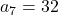
- किसी A.P. के प्रथम
 पदों का योग
पदों का योग 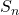 सूत्र
सूत्र![Rendered by QuickLaTeX.com S_n=\frac{n}{2}[2a+(n-1)d]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-1c9f4224b854734d965fb75823addeed_l3.png)
से प्राप्त होता है। - यदि एक परिमित A.P. का अंतिम पद (मान लीजिए
 वाँ पद)
वाँ पद)  है, तो इस A.P. के सभी पदों का योग सूत्र
है, तो इस A.P. के सभी पदों का योग सूत्र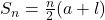
होता है। - **प्रथम
 धन पूर्णांकों का योग सूत्र**
धन पूर्णांकों का योग सूत्र**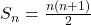
- यदि
 , समांतर श्रेढ़ी में हैं तब
, समांतर श्रेढ़ी में हैं तब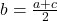
यहाँ ,
,  और
और  का **समांतर माध्य** कहलाता है।
का **समांतर माध्य** कहलाता है। - प्रथम 25 धन पूर्णांकों का योग ज्ञात करना।
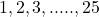 पदों तक
पदों तक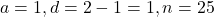
![Rendered by QuickLaTeX.com S_n=\frac{n}{2}[2a+(n-1)d]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-1c9f4224b854734d965fb75823addeed_l3.png)
![Rendered by QuickLaTeX.com S_{25}=\frac{25}{2}[2\times1+(25-1)\times1]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-5a92835119876790af9c4ce869be0b79_l3.png)
![Rendered by QuickLaTeX.com S_{25}=\frac{25}{2}[2+24]](https://mpeducator.co.in/wp-content/ql-cache/quicklatex.com-6f3f271c493528fbafbaa016d4627da4_l3.png)
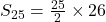
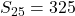
अध्याय- 6
त्रिभुज
अवधारणाओ पर आधरित महत्वपूर्ण तथ्य
y ऐसी आकृतियाँ जिनके आकार (Shape) समान हों, उनका आमाप (size) समान हो या न हो समरूप आकृतियाँ कहलाती हैं ।
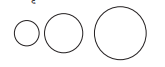
तीनों वृत्त हैं, इनके आकार समान हैं परन्तु इनके आमाप अलग-अलग हैं, अतः, यह समरूप आकृतियाँ हैं।”
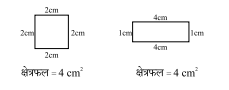
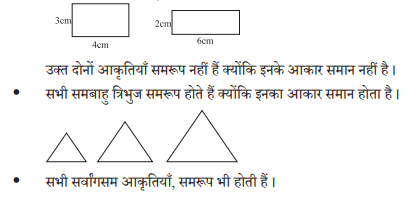
उक्त दोनों आकृतियों के माप (क्षेत्रफल) समान हैं परंतु आकार अलग-अलग हैं, अत: वर्ग एवं आयत समरूप आकृतियाँ नहीं हैं ।
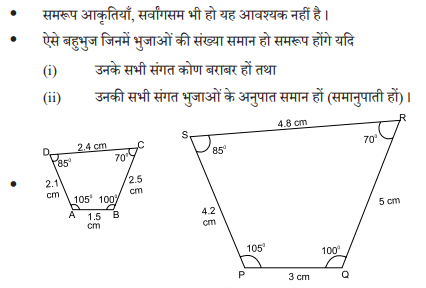
y सभी वर्ग समरूप होते हैं ।
y सभी आयत समरूप हों, यह आवश्यक नहीं है ।
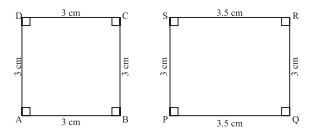
- चतुर्भुज
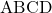 व चतुर्भुज
व चतुर्भुज 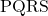 में
में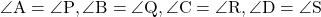
सभी संगत कोण समान हैं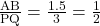
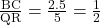
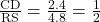
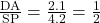
यहाँ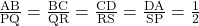
संगत भुजाओं के अनुपात भी समान हैं अतः:
चतुर्भुज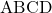 व चतुर्भुज
व चतुर्भुज 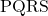 समरूप हैं।
समरूप हैं।
- त्रिभुजों की समरूपता की शर्त –
(i) उनके संगत कोण बराबर हों।
(ii) उनकी संगत भुजाओं के अनुपात बराबर हों। - त्रिभुजों की समरूपता की कसौटियाँ – दो त्रिभुजों को समरूप दर्शाने के लिए निम्न कसौटियों का प्रयोग किया जा सकता है –
(i) **भुजा – भुजा – भुजा** (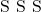 )
)
यदि दो त्रिभुजों की संगत तीनों भुजाओं के अनुपात बराबर हों तो वे त्रिभुज समरूप होंगे।
(ii) **भुजा कोण भुजा** (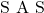 )
)
यदि एक त्रिभुज का एक कोण दूसरे त्रिभुज के एक कोण के बराबर हो तथा इन कोणों को अंतर्गत करने वाली भुजाएँ एक ही अनुपात में हों तो दोनों त्रिभुज समरूप होते हैं।
(iii) **कोण कोण कोण** (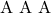 )
)
यदि दो त्रिभुजों के सभी (तीनों) संगत कोणों की माप बराबर हो तो त्रिभुज समरूप होंगे।
(iv) **कोण-कोण** ( )
)
यदि दो त्रिभुजों में एक त्रिभुज के दो कोण क्रमश: दूसरे त्रिभुज के दो कोणों के बराबर हों, तो दोनों त्रिभुज समरूप होते हैं।
- चतुर्भुज
 व चतुर्भुज
व चतुर्भुज  में
में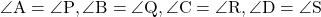
सभी संगत कोण समान हैं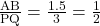
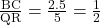
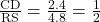
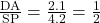
यहाँ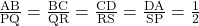
संगत भुजाओं के अनुपात भी समान हैं अतः:
चतुर्भुज व चतुर्भुज
व चतुर्भुज  समरूप हैं।
समरूप हैं। - त्रिभुजों की समरूपता की शर्त –
(i) उनके संगत कोण बराबर हों।
(ii) उनकी संगत भुजाओं के अनुपात बराबर हों। - त्रिभुजों की समरूपता की कसौटियाँ – दो त्रिभुजों को समरूप दर्शाने के लिए निम्न कसौटियों का प्रयोग किया जा सकता है –
(i) **भुजा – भुजा – भुजा** (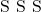 )
)
यदि दो त्रिभुजों की संगत तीनों भुजाओं के अनुपात बराबर हों तो वे त्रिभुज समरूप होंगे।
(ii) **भुजा कोण भुजा** (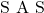 )
)
यदि एक त्रिभुज का एक कोण दूसरे त्रिभुज के एक कोण के बराबर हो तथा इन कोणों को अंतर्गत करने वाली भुजाएँ एक ही अनुपात में हों तो दोनों त्रिभुज समरूप होते हैं।
(iii) **कोण कोण कोण** (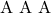 )
)
यदि दो त्रिभुजों के सभी (तीनों) संगत कोणों की माप बराबर हो तो त्रिभुज समरूप होंगे।
(iv) **कोण-कोण** ( )
)
यदि दो त्रिभुजों में एक त्रिभुज के दो कोण क्रमश: दूसरे त्रिभुज के दो कोणों के बराबर हों, तो दोनों त्रिभुज समरूप होते हैं।
- यदि दो त्रिभुज सर्वांगसम हैं तो वे समरूप भी होंगे। दो त्रिभुज यदि समरूप हैं तो वह सर्वांगसम हो भी सकते हैं और नहीं भी।
- दो समान कोणिक त्रिभुजों की संगत भुजाएँ **समानुपातिक** होती हैं।
या
दो समान कोणिक त्रिभुजों में उनकी संगत भुजाओं का अनुपात सदैव **समान** होता है। - **आधारभूत आनुपातिकता (थेल्स) प्रमेय कथन**: “त्रिभुज की एक भुजा के समांतर खींची गई रेखा अन्य दो भुजाओं को समान अनुपात में विभाजित करती है।”
त्रिभुज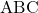 में भुजा
में भुजा 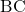 के समांतर खींची गई रेखा
के समांतर खींची गई रेखा 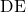 , अन्य दोनों भुजाओं
, अन्य दोनों भुजाओं 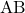 व
व 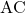 को समानुपात में विभाजित करेगी, अर्थात
को समानुपात में विभाजित करेगी, अर्थात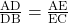
- **थेल्स प्रमेय का विलोम**: किसी त्रिभुज में किन्हीं भुजाओं को समानुपात में विभाजित करने वाली रेखा, तीसरी भुजा के समांतर होती है।
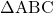 में यदि रेखा
में यदि रेखा 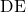 , भुजा
, भुजा 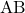 व
व 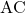 को समानुपात में विभाजित करती है अर्थात
को समानुपात में विभाजित करती है अर्थात 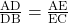 हो तो
हो तो 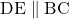 होगी।
होगी। 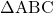 में
में 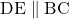 है तो थेल्स प्रमेय से
है तो थेल्स प्रमेय से
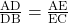
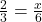
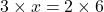
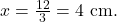
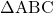 में
में
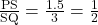
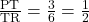
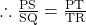
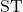 रेखा भुजाओं
रेखा भुजाओं 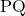 व
व 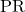 को समान अनुपात में विभाजित करती है।
को समान अनुपात में विभाजित करती है।
अतः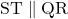 (थेल्स प्रमेय के विलोम से)
(थेल्स प्रमेय के विलोम से)- प्रसिद्ध यूनानी गणितज्ञ थेल्स का समय काल सा.यु.पू. 640 – 546 है।
For any Pdf for 9th to 12th kindly visit : MPBoardPd
2 thoughts on “MP Board 10th Mathematics One Liner part 1:महत्वपूर्ण गणितीय तथ्यों से गणित की पढ़ाई हुई आसान”